1. 问题描述
给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1]
输出:[1,2,3,5]
示例 2:
输入:nums = [5,1,1,2,0,0]
输出:[0,0,1,1,2,5]
提示:
1 <= nums.length <= 50000
-50000 <= nums[i] <= 50000
2. 思路
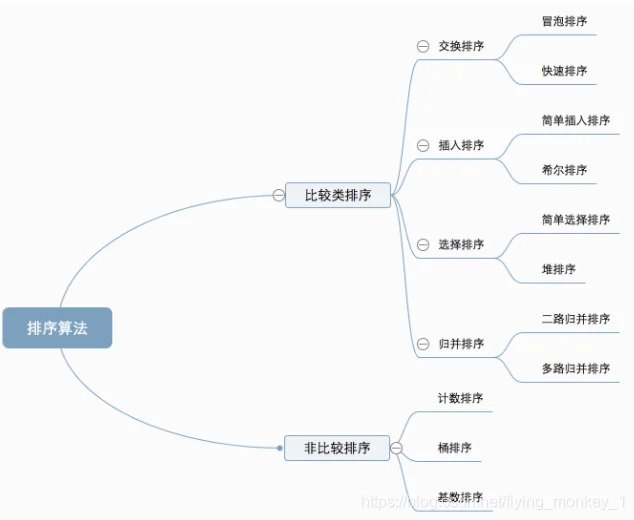
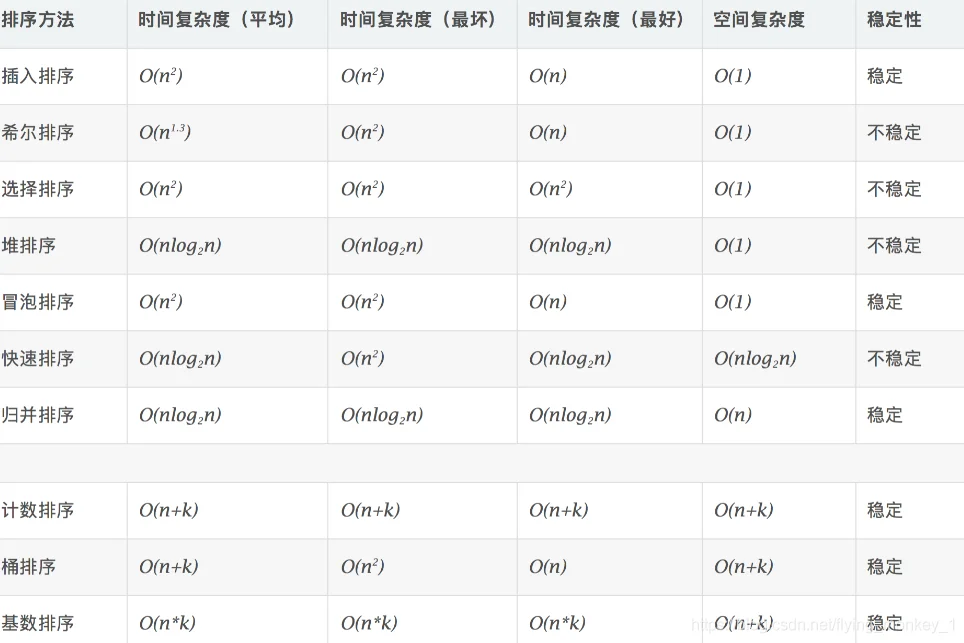
3. 代码
3.1. 冒泡排序:超时
func sortArray(nums []int) []int {
for i := 0; i < len(nums); i++ {
for j := 0; j < len(nums) - i - 1; j++ {
if nums[j] > nums[j + 1] {
nums[j], nums[j + 1] = nums[j + 1], nums[j]
}
}
}
return nums
}
3.2. 快排(通过)
要点:分区: 指对于任意一个元素pivot,将它移动到它应该所在位置的过程。分区有两种思路:同向双指针,反向双指针。
func sortArray(nums []int) []int {
quickSort(nums, 0, len(nums) - 1)
return nums
}
func quickSort(nums []int, l int, r int) {
if l >= r {
return
}
pivotLocation := partition(nums, l, r)
quickSort(nums, l, pivotLocation - 1)
quickSort(nums, pivotLocation + 1, r)
}
func partition(nums []int, l int, r int) int {
pivot := nums[l]
for l < r {
for l < r && nums[r] >= pivot {
r--
}
nums[l] = nums[r]
for l < r && nums[l] <= pivot {
l++
}
nums[r] = nums[l]
}
nums[l] = pivot
return l
}
func sortArray(nums []int) []int {
quickSort(nums, 0, len(nums) - 1)
return nums
}
func quickSort(nums []int, L int, R int) {
if L >= R {
return
}
pivotIndex := partition(nums, L, R)
// fmt.Println(pivotIndex)
quickSort(nums, L, pivotIndex - 1)
quickSort(nums, pivotIndex + 1, R)
}
func partition(nums []int, L int, R int) int {
pivot := nums[L]
slow, fast := L + 1, L + 1
// right := left + 1
for fast <= R {
if nums[fast] < pivot {
nums[slow], nums[fast] = nums[fast], nums[slow]
// fmt.Printf("%v,%v\n",slow, fast)
fast++
slow++
} else {
fast++
}
}
nums[L] = nums[slow - 1]
nums[slow-1] = pivot
return slow - 1
}
3.3. 直接插入(通过)
要点: 从后向前比
func sortArray(nums []int) []int {
for i := 1; i < len(nums); i++ {
for j := i; j > 0; j-- {
if nums[j - 1] > nums[j] {
nums[j - 1], nums[j] = nums[j], nums[j - 1]
}
}
}
return nums
}
3.4. 希尔排序(通过)
要点: 先宏观,再微观
func sortArray(nums []int) []int {
// 使用 Knuth 增量序列,找增量的最大值
h := 1
for 3 * h + 1 < len(nums) {
h = 3 * h + 1
}
for h >= 1 {
// 间隔为h的,插入排序
for i := h; i < len(nums); i += h{
for j := i; j > 0; j -= h {
if nums[j - h] > nums[j] {
nums[j], nums[j - h] = nums[j - h], nums[j]
}
}
}
h = h / 3
}
return nums
}
3.5. 选择排序(通过)
要点:每一轮都选出一个最小值对应的索引
func sortArray(nums []int) []int {
for i := 0; i < len(nums) - 1; i++ {
minIndex := i
for j := i + 1; j < len(nums); j++ {
if nums[j] < nums[minIndex] {
minIndex = j
}
}
nums[i], nums[minIndex] = nums[minIndex], nums[i]
}
return nums
}
3.8. 堆排序(重点,通过)
- 堆排序是选择排序的优化,选择排序需要在未排定的部分里通过「打擂台」的方式选出最大的元素(复杂度 O(N)O(N)),而「堆排序」就把未排定的部分构建成一个「堆」,这样就能以 O(logN) 的方式选出最大元素;
- 堆是一种相当有意思的数据结构,它在很多语言里也被命名为「优先队列」。它是建立在数组上的「树」结构(二叉堆是建立在完全二叉树的基础上),类似的数据结构还有「并查集」「线段树」等。
- 优先队列」是一种特殊的队列,按照优先级顺序出队,从这一点上说,与「普通队列」无差别。「优先队列」可以用数组实现,也可以用有序数组实现,但只要是线性结构,复杂度就会高,因此,「树」结构就有优势,「优先队列」的最好实现就是「堆」
堆相关的操作有:
- make_heap()创建堆
- push_heap()向堆中添加元素
- pop_heap()删除堆顶数据
- sort_heap()堆排序
要点:
- 将数组中的元素组织成大顶堆
- 堆顶元素和最后一个元素互换,循环调整为大顶堆
func sortArray(nums []int) []int {
heapify(nums)
for i := len(nums) - 1; i >= 1; {
nums[i], nums[0] = nums[0], nums[i]
i--
siftDown(nums, 0, i)
}
return nums
}
func heapify(nums []int) {
// 从最后一个非叶子节点向上,下沉,调整为大顶堆
for i := len(nums) / 2 - 1; i >= 0; i-- {
siftDown(nums, i, len(nums) - 1)
}
}
// 第k个元素下沉
func siftDown(nums []int, k int, end int) {
for 2 * k + 1 <= end {
j := 2 * k + 1
if j+1 <= end && nums[j+1] > nums[j]{
j++
}
if nums[j] > nums[k] {
nums[j], nums[k] = nums[k], nums[j]
} else {
break
}
k = j
}
}
3.7. 归并排序(重点,通过)
不知道问题在哪里
func sortArray(nums []int) []int {
temp := make([]int, len(nums))
mergeSort(nums, 0, len(nums) - 1, temp)
return nums
}
func mergeSort(nums []int, l int, r int, temp []int) {
if l >= r {
return
}
mid := (l+r)>>1
mergeSort(nums, l, mid, temp)
mergeSort(nums, mid + 1, r, temp)
// 合并两个有序数组
merge(nums, l, mid, r, temp)
}
func merge(nums []int, l int, mid int, r int, temp []int) {
i := l
j := mid + 1
k := 0
e := r
for i <= mid && j <= e {
if nums[i] < nums[j] {
temp[k] = nums[i]
i++
k++
} else {
temp[k] = nums[j]
j++
k++
}
}
temp = temp[0:k]
if i >= mid {
temp = append(temp, nums[j:]...)
}
if j >= e {
temp = append(temp, nums[i:mid+1]...)
}
for ii := 0; ii < len(temp); ii++ {
nums[ii] = temp[ii]
}
}
通过版本
func sortArray(nums []int) []int {
if len(nums) < 2 {
return nums
}
mid := len(nums) / 2
left := sortArray(nums[:mid])
right := sortArray(nums[mid:])
res := merge(left, right)
return res
}
func merge(left []int, right []int) []int {
i := 0
j := 0
l := len(left)
r := len(right)
res := make([]int, 0)
for i < l && j < r {
if left[i] > right[j] {
res = append(res, right[j])
j++
} else {
res = append(res, left[i])
i++
}
}
if i < len(left) {
res = append(res, left[i:]...)
}
if j < len(right) {
res = append(res, right[j:]...)
}
return res
}
