一个问题的解可以被拆分成多个子问题的解
拆分前的原问题与拆分后的子问题除了数据规模不同,求解思路完全一样
子问题存在递归终止条件
递归函数及编写思路
很多编程语言都支持递归函数,所谓递归函数指的是在函数内部调用函数自身的函数,从数学解题思路来说,递归就是把一个大问题拆分成多个小问题,再各个击破,在实际开发过程中,某个问题满足以下条件就可以通过递归函数来解决:
需要注意的是,编写递归函数时,这个递归一定要有终止条件,否则就会无限调用下去,直到内存溢出。所以我们可以归纳出递归函数的编写思路:抽象出递归模型(可以被复用到子问题的模式/公式),同时找到终止条件。
通过斐波那契数列求解演示
下面我们就以递归函数的经典示例 —— 斐波那契数列为例,演示如何通过 Go 语言基于上述归纳的思路编写递归函数来打印斐波那契数列。
斐波那契数列的前几个数字是这样的:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233...
我们可以通过这些数字的排列规律总结出对应的计算公式:
F(1) = 0
F(2) = 1
F(3) = 1
F(4) = 2
F(5) = 3
...
F(n) = F(n-1) + F(n-2) (n > 2)
即从第三个数字开始,对应的数值是前面两个数字的和,其中 n 表示数字在斐波那契数列中的序号,最后一个公式就是递归模型,通过这个公式就可以把求解斐波那契数列的问题拆分为多个子问题来处理:即把求解 F(n) 的值拆分为求解 F(n-1) 和 F(n-2) 两个子问题返回值的和,以此类推,直到到达终止条件 —— 当 n=2 时,返回数值 1,当 n=1 时,返回数值 0。
显然这是一个递归处理的过程,我们根据这个思路编写对应的递归函数 fibonacci 实现如下:
func fibonacci(n int) int {
if n == 1 {
return 0
}
if n == 2 {
return 1
}
return fibonacci(n-1) + fibonacci(n-2)
}
我们可以这么调用这个函数返回指定序号对应的斐波那契数值:
func main() {
n := 5
num := fibonacci(n)
fmt.Printf("The %dth number of fibonacci sequence is %d\n", n, num)
}
上述代码的打印的结果是:

递归函数性能优化
递归函数执行耗时对比
递归函数是层层递归嵌套执行的,如果层级不深,比如上面这种,很快就会返回结果,但如果传入一个更大的序号,比如 50,就会明显感觉到延迟。
为了更直观地对比耗时差异,我们参照上篇教程实现一个斐波那契函数版的耗时计算函数 fibonacciExecTime,然后通过装饰器模式调用 fibonacci 函数:
package main
import (
"fmt"
"time"
)
type FibonacciFunc func(int) int
// 通过递归函数实现斐波那契数列
func fibonacci(n int) int {
// 终止条件
if n == 1 {
return 0
}
if n == 2 {
return 1
}
// 递归公式
return fibonacci(n-1) + fibonacci(n-2)
}
// 斐波那契函数执行耗时计算
func fibonacciExecTime(f FibonacciFunc) FibonacciFunc {
return func(n int) int {
start := time.Now() // 起始时间
num := f(n) // 执行斐波那契函数
end := time.Since(start) // 函数执行完毕耗时
fmt.Printf("--- 执行耗时: %v ---\n", end)
return num // 返回计算结果
}
}
func main() {
n1 := 5
f := fibonacciExecTime(fibonacci)
r1 := f(n1)
fmt.Printf("The %dth number of fibonacci sequence is %d\n", n1, r1)
n2 := 50
r2 := f(n2)
fmt.Printf("The %dth number of fibonacci sequence is %d\n", n2, r2)
}
当然,为了实现更加通用的函数执行耗时计算功能,应该将 FibonacciFunc 函数参数和返回值声明为泛型,后面在介绍完泛型实现之后,你可以回过头来重新实现一下。
具体细节我就不一一解释了,如果你理解了 Go 装饰器模式的实现,很容易理解这段代码。上述代码的最终打印结果如下:
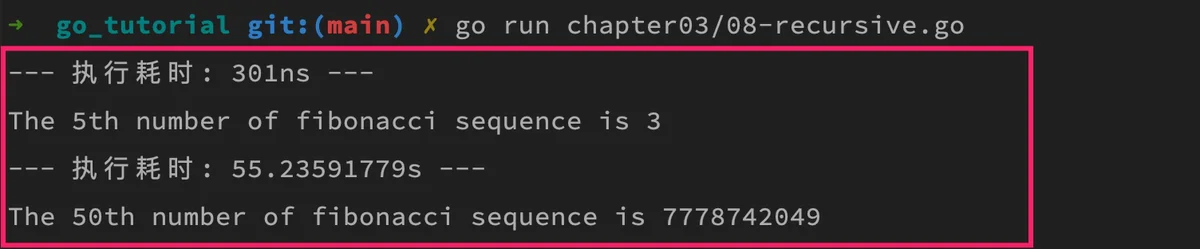
可以看到,虽然 5 和 50 从序号上看只相差了 10 倍,但是最终体现在递归函数的执行时间上,却是不止十倍百倍的巨大差别(1s = 10亿ns)。
究其原因,一方面是因为递归函数调用产生的额外开销,另一方面是因为目前这种实现存在着重复计算,比如我在计算 fibonacci(50) 时,会转化为计算 fibonacci(49) 与 fibonacci(48) 之和,然后我在计算 fibonacci(49) 时,又会转化为调用 fibonacci(48) 与 fibonacci(47) 之和,这样一来 fibonacci(48) 就会两次重复计算,这一重复计算就是一次新的递归(从序号 48 递归到序号 1),以此类推,大量的重复递归计算堆积,最终导致程序执行缓慢。
通过内存缓存技术优化递归函数性能
我们先对后一个原因进行优化,通过缓存中间计算结果来避免重复计算,从而提升递归函数的性能。
按照这个思路我们来重写下递归函数 fibonacci 的实现:
const MAX = 50
var fibs [MAX]int
// 缓存中间结果的递归函数优化版
func fibonacci2(n int) int {
if n == 1 {
return 0
}
if n == 2 {
return 1
}
index := n - 1
if fibs[index] != 0 {
return fibs[index]
}
num := fibonacci2(n-1) + fibonacci2(n-2)
fibs[index] = num
return num
}
这一次,我们会通过预定义数组 fibs 保存已经计算过的斐波那契序号对应的数值(序号 n 与对应数组索引的映射关系为 n-1,因为数组索引从下标 0 开始,而这里的斐波那契序号从 1 开始),这样下次要获取对应序号的斐波那契值时会直接返回而不是调用一次递归函数进行计算。
将调用代码调整如下:
func main() {
n1 := 5
f1 := fibonacciExecTime(fibonacci)
r1 := f1(n1)
fmt.Printf("The %dth number of fibonacci sequence is %d\n", n1, r1)
n2 := 50
r2 := f1(n2)
fmt.Printf("The %dth number of fibonacci sequence is %d\n", n2, r2)
f2 := fibonacciExecTime(fibonacci2)
r3 := f2(n2)
fmt.Printf("The %dth number of fibonacci sequence is %d\n", n2, r3)
}
印结果耗时对比可以看出,之前执行慢主要是重复的递归计算导致的(1µs=1000ns,所以其性能和 fibonacci(5) 是在一个数量级上):
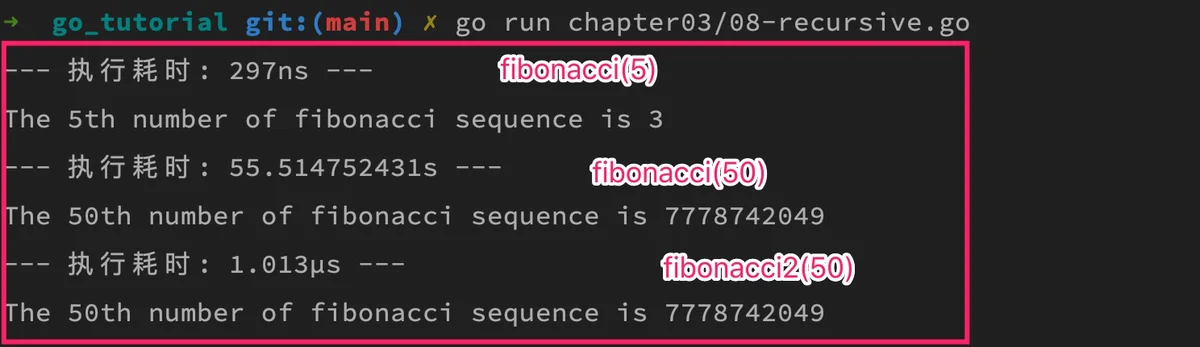
这种优化是在内存中保存中间结果,所以称之为内存缓存技术(memoization),这种内存缓存技术在优化计算成本相对昂贵的函数调用时非常有用。
通过尾递归优化递归函数性能
接下来,我们来看能否对造成上述递归函数性能低下的第一个原因进行优化。
我们知道函数调用底层是通过栈来维护的,对于递归函数而言,如果层级太深,同时保存成百上千的调用记录,会导致这个栈越来越大,消耗大量内存空间,严重情况下会导致栈溢出(stack overflow),为了优化这个问题,可以引入尾递归优化技术来重用栈,降低对内存空间的消耗,提升递归函数性能。
尾递归优化是函数式编程的重要特性之一,在了解尾递归优化前,我们先来看看什么是尾递归。
在计算机科学里,尾调用是指一个函数的最后一个动作是调用一个函数(只能是一个函数调用,不能有其他操作,比如函数相加、乘以常量等):
func f(x int) int {
...
return g(x);
}
这种情况下称该调用位置为尾位置,若这个函数在尾位置调用自身,则称这种情况为尾递归,它是尾调用的一种特殊情形。尾调用的一个重要特性是它不是在函数调用栈上添加一个新的堆栈帧 —— 而是更新它,尾递归自然也继承了这一特性,这就使得原来层层递进的调用栈变成了线性结构,因而可以极大优化内存占用,提升程序性能,这就是尾递归优化技术。
以计算斐波那契数列的递归函数为例,简单来说,就是处于函数尾部的递归调用前面的中间状态都不需要再保存了,这可以节省很大的内存空间,在此之前的代码实现中,递归调用 fibonacci(n-1) 时,还有 fibonacci(n-2) 没有执行,因此需要保存前面的中间状态,内存开销很大。
一些编程语言的编译器提供了对尾递归优化的支持,但是 Go 目前并不支持,为了使用尾递归优化技术,需要手动编写实现代码。
尾递归的实现需要重构之前的递归函数,确保最后一步只调用自身,要做到这一点,就要把所有用到的内部变量/中间状态变成函数参数,以 fibonacci 函数为例,就是 fibonacci(n-1) 和 fibonacci(n-2),我们可以这样实现尾递归函数 fibonacciTail:
func fibonacciTail(n, first, second int) int {
if n < 2 {
return first
}
return fibonacciTail(n-1, second, first+second)
}
当前 first + second 的和赋值给下次调用的 second 参数,当前 second 值赋值给下次调用的 first 参数,就等同于实现了 F(n) = F(n-1) + F(n-2) 的效果,循环往复,不断累加,直到 n 值等于 1(F(1) = 0,无需继续迭代下去),则返回 first 的值,也就是最终的 F(n) 的值。
简单来说,就是把原来通过递归调用计算结果转化为通过外部传递参数初始化,再传递给下次尾递归调用不断累加,这样就可以保证 fibonacciTail 调用始终是线性结构的更新,不需要开辟新的堆栈保存中间函数调用。
但是从语义上看这个新的斐波那契函数有点怪,我们可以在外面套一层:
func fibonacci3(n int) int {
return fibonacciTail(n, 0, 1) // F(1) = 0, F(2) = 1
}
这样,就可以像之前一样调用 fibonacci3 计算在斐波那契数列中序号 n 的值了:
func main() {
n1 := 5
f1 := fibonacciExecTime(fibonacci)
r1 := f1(n1)
fmt.Printf("The %dth number of fibonacci sequence is %d\n", n1, r1)
n2 := 50
r2 := f1(n2)
fmt.Printf("The %dth number of fibonacci sequence is %d\n", n2, r2)
f2 := fibonacciExecTime(fibonacci2)
r3 := f2(n2)
fmt.Printf("The %dth number of fibonacci sequence is %d\n", n2, r3)
f3 := fibonacciExecTime(fibonacci3)
r4 := f3(n2)
fmt.Printf("The %dth number of fibonacci sequence is %d\n", n2, r4)
}
执行上述代码,打印结果如下:
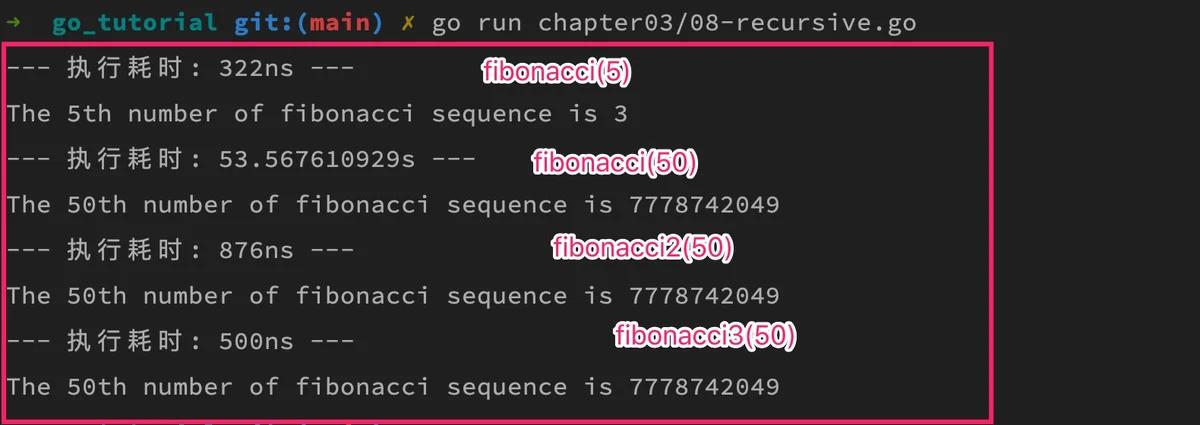
可以看到,尾递归优化版递归函数性能要优于内存缓存技术优化版,并且不需要借助额外的内存空间保存中间结果,因此从性能角度看是更好的选择,就是可读性差一些,理解起来有些困难。

