一 LowB三人组
1.1 冒泡排序
冒泡排序(Bubble Sort),是一种计算机科学领域的较简单的排序算法。它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果顺序(如从大到小、首字母从Z到A)错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换,也就是说该元素列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名“冒泡排序”。
示意图:
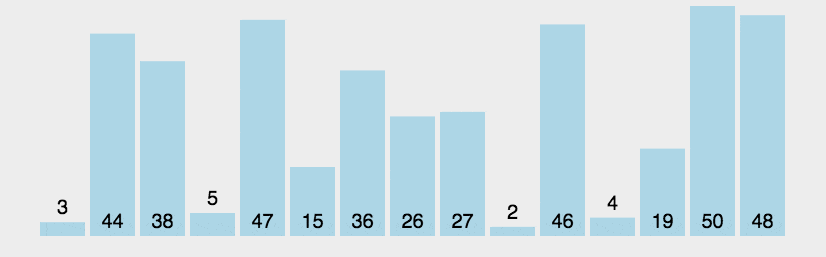
排序思想:
- 有n个数需要被排序;假设先选取第0个位置的数字和让其和后一位的数进行比较;
- 如果比较时发现当前数比后一个数大(即比较时,出现不符合我们规则的顺序),交换两数;
- 然后选第1个位置的数字,继续遍历,一轮后,即可找出一个最大数;(即最后一位已经到达其应在位置)最后一个数已经不需要参与后面的比较了;
- 继续遍历,则每轮比较后,最后一个数就会到达其应到位置;
- 每轮能找出一个最大的数,则最多仅需n-1轮即可全部排序完成;因为其余数排序好后,最后一个数不用在找自己的位置了;(i表示外层for循环表示轮数)
- 每轮选中的数下标为j,从0开始;
因为选中的数和后一个比较,最后一个不用选中,所以j的上限 -1;
又因为每过1轮,最后一个数就会被定下来,所以每轮j的上限 -i;
代码实现:
package main
import (
"fmt"
)
func main() {
//1.定义测试数组
var intArr = [...]int{10, 5, 11, 9, 0} //test01
//2.输出排序前数组;
fmt.Println("排序前:", intArr)
for i := 0; i < len(intArr)-1; i++ {
//3.如果一轮遍历比较后,没有发生过交换,则当前每一个数都比他后面的数小,
//即当前数组已有序;则立即可停止排序;
//定义 is_changed ,记录每轮发生过交换;
var is_changed bool
for j := 0; j < len(intArr)-1-i; j++ {
if intArr[j+1] < intArr[j] {
//如果顺序不对,则发生交换,字段变为 true;
is_changed = true
//交换两数位置;
intArr[j] = intArr[j+1] ^ intArr[j]
intArr[j+1] = intArr[j+1] ^ intArr[j]
intArr[j] = intArr[j+1] ^ intArr[j]
}
}
fmt.Printf("经过%v轮遍历;冒泡排序后结果为:%v\n", i+1, intArr)
//如果一整轮没交换过,则已经有序;退出排序;
if is_changed == false {
fmt.Printf("现在已经有序,直接停止;\n")
break
}
}
}
运行结果:
[Running] go run "e:\golang开发学习\go_pro\test.go"
排序前: [10 5 11 9 0]
经过1轮遍历;冒泡排序后结果为:[5 10 9 0 11]
经过2轮遍历;冒泡排序后结果为:[5 9 0 10 11]
经过3轮遍历;冒泡排序后结果为:[5 0 9 10 11]
经过4轮遍历;冒泡排序后结果为:[0 5 9 10 11]
[Done] exited with code=0 in 2.41 seconds
1.2 选择排序
选择式排序也属于内部排序法,是从欲排序的数据中,按指定的规则选出某一元素,经过和其他元素重整,再依原则交换位置后达到排序的目的。
示意图:
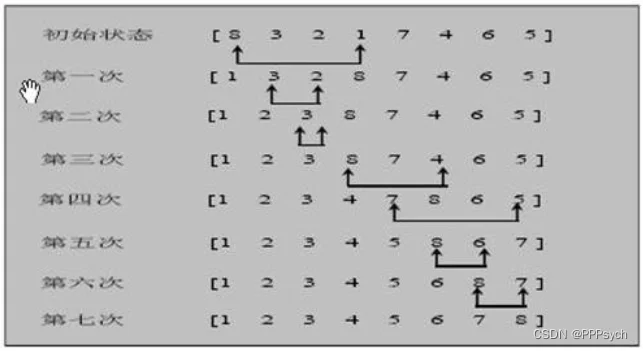
排序思想:
- 第一次从 R[0]~R[n-1]中选取最小值,与 R[0]交换,
- 第二次从 R[1]~R[n-1]中选取最小值,与 R[1]交换,
- 第三次从 R[2]~R[n-1]中选取最小值,与 R[2]交换,…,
- 第 i 次从 R[i-1]~R[n-1]中选取最小值,与 R[i-1]交换,…,
- 第 n-1 次从R[n-2]~R[n-1]中选取最小值,与 R[n-2]交换,
- 总共通过 n-1 次,得到一个按排序码从小到大排列的有序序列。
代码实现:
package main
import (
"fmt"
"math/rand"
"time"
)
func Select_Sort(arr []int) {
for i := 0; i < len(arr)-1; i++ {
// 假设最小值是无序区的第一个位置
min_loc := i
// 自己不用跟自己比较
for j := i + 1; j < len(arr); j++ {
if arr[min_loc] > arr[j] {
min_loc = j
}
}
arr[min_loc], arr[i] = arr[i], arr[min_loc]
}
}
// 生成随机int切片 正整数 rand.Intn返回一个非负伪随机数[0,n)作为int。如果n <= 0则报错
func rand_array(arr []int, min int, max int) {
if min >= max || min == 0 || max == 0 {
fmt.Println("输入最大, 最小值有误!")
return
}
// 如果不加这个 每次会生成一样的
rand.Seed(time.Now().Unix())
for i := 0; i < len(arr); i++ {
arr[i] = rand.Intn(max-min) + min
}
}
func main() {
min := 5
max := 100
var mylist []int = make([]int, 10)
rand_array(mylist, min, max)
fmt.Printf("随机的int 切片为:%d\n", mylist)
Select_Sort(mylist)
fmt.Printf("选择排序后的int 切片为:%d\n", mylist)
}
运行结果:
[Running] go run "e:\golang开发学习\go_pro\test.go"
随机的int 切片为:[29 50 37 36 70 19 56 64 66 88]
选择排序后的int 切片为:[19 29 36 37 50 56 64 66 70 88]
[Done] exited with code=0 in 1.246 seconds
1.3 插入排序
插入式排序属于内部排序法,是对于欲排序的元素以插入的方式找寻该元素的适当位置,以达到排序的目的
示意图:

排序思想:
- 把 n 个待排序的元素看成为一个有序表和一个无序表,
- 开始时有序表中只包含一个元素,无序表中包含有 n-1 个元素,
- 排序过程中每次从无序表中取出第一个元素,把它的排序码依次与有序表元素的排序码进行比较,将它插入到有序表中的适当位置,使之成为新的有序表。
代码实现:
package main
import "fmt"
func Insert_Sort(arr *[7]int) {
for i := 1; i < len(arr); i++ {
inserVal := arr[i]
inserIndex := i - 1 //下标
//从大到小
for inserIndex >= 0 && arr[inserIndex] < inserVal {
arr[inserIndex+1] = arr[inserIndex] //数据后移
inserIndex--
}
//插入
if inserIndex+1 != i {
arr[inserIndex+1] = inserVal
}
fmt.Printf("第%d此插入后: %v\n", i, *arr)
}
}
func main() {
arr := [7]int{23, 0, 12, 56, 34, -1, 55}
fmt.Println("原始数组为:", arr)
Insert_Sort(&arr)
fmt.Println(arr)
}
运行结果:
[Running] go run "e:\golang开发学习\go_pro\test.go"
原始数组为: [23 0 12 56 34 -1 55]
第1此插入后: [23 0 12 56 34 -1 55]
第2此插入后: [23 12 0 56 34 -1 55]
第3此插入后: [56 23 12 0 34 -1 55]
第4此插入后: [56 34 23 12 0 -1 55]
第5此插入后: [56 34 23 12 0 -1 55]
第6此插入后: [56 55 34 23 12 0 -1]
[56 55 34 23 12 0 -1]
[Done] exited with code=0 in 1.666 seconds
2.1 快速排序
快速排序(Quicksort)是对冒泡排序的一种改进。
排序思想:
- 通过一趟排序将要排序的数据分割成独立的两部分,
- 其中一部分的所有数据都比另外一部分的所有数据都要小,
- 然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列
示意图:
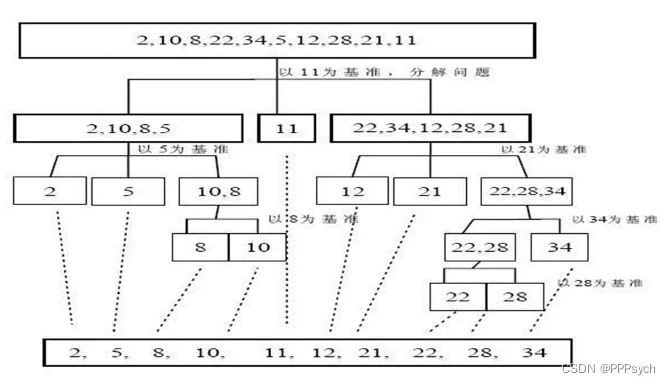
应用实例:
要求:对 [-9,78,0,23,-567,70] 进行从小到大的排序
说明 [ 验证分析 ]:
- 如果取消左右递归,结果是:-9 -567 0 23 78 70
- 如果取消右递归,结果是: -567 -9 0 23 78 70
- 如果取消左递归,结果是:-9 -567 0 23 70 78
代码实现:
package main
import (
"fmt"
)
//快速排序
//说明
//1. left 表示 数组左边的下标
//2. right 表示数组右边的下标
//3 array 表示要排序的数组
func QuickSort(left int, right int, array *[9]int) {
l := left
r := right
// pivot 是中轴, 支点
pivot := array[(left+right)/2]
temp := 0
//for 循环的目标是将比 pivot 小的数放到 左边
// 比 pivot 大的数放到 右边
for l < r {
//从 pivot 的左边找到大于等于 pivot 的值
for array[l] < pivot {
l++
}
//从 pivot 的右边边找到小于等于 pivot 的值
for array[r] > pivot {
r--
}
// 1 >= r 表明本次分解任务完成, break
if l >= r {
break
}
//交换
temp = array[l]
array[l] = array[r]
array[r] = temp
//优化
if array[l] == pivot {
r--
}
if array[r] == pivot {
l++
}
}
// 如果 1== r, 再移动下
if l == r {
l++
r--
}
// 向左递归
if left < r {
QuickSort(left, r, array)
}
// 向右递归
if right > l {
QuickSort(l, right, array)
}
}
func main() {
arr := [9]int{-9, 78, 0, 23, -567, 70, 123, 90, -23}
fmt.Println("初始", arr)
//调用快速排序
QuickSort(0, len(arr)-1, &arr)
fmt.Println("排序后:")
fmt.Println(arr)
}
运行结果:
[Running] go run "e:\golang开发学习\go_pro\test.go"
初始 [-9 78 0 23 -567 70 123 90 -23]
排序后:
[-567 -23 -9 0 23 70 78 90 123]
[Done] exited with code=0 in 1.044 seconds
2.2 堆排序
2.2.1 堆的概念
大顶堆小顶堆2.2.2 堆的性质
numslengleng/2-1nln = n*2+1rn = n*2+2lnrnleng-12.2.3 最大堆实现
-
先将数组以此插入完全二叉树中,形成一颗完全二叉树。
-
堆的构建是从右往左、自下而上的。从最后一个节点的父节点leng/2-1开始依次递减。
-
判断左右子节点的是否存在
-
判断是否需要替换。子节点的值是否大于当前节点的值
-
如果替换,那么被替换的子节点也要左一次堆的构建
-
得到个堆
最大堆实现细节(两个操作):
- push:向堆中插入数据时,首先在堆的末尾插入数据,如果该数据比父亲节点还大,那么交换,然后不断向上提升,直到没有大小颠倒为止。
- pop:从堆中删除最大值时,首先把最后一个值复制到根节点上,并且删除最后一个数值,然后和儿子节点比较,如果值小于儿子,与儿子节点交换,然后不断向下交换, 直到没有大小颠倒为止。在向下交换过程中,如果有两个子儿子都大于自己,就选择较大的。
最大堆有两个核心操作,一个是上浮,一个是下沉,分别对应 push 和 pop。
操作一次 push 的最好时间复杂度为:O(1),因为第一次上浮时如果不大于父亲,那么就结束了。最坏的时间复杂度为: O(logn),相当于每次都大于父亲,会一直往上浮到根节点,翻转次数等于树的高度,而树的高度等于元素个数的对数:log(n)。
2.2.4 创建堆
package main
import (
"fmt"
)
// 一个最大堆,一棵完全二叉树
// 最大堆要求节点元素都不小于其左右孩子
type Heap struct {
Size int // 堆的大小
// 使用内部的数组来模拟树
// 一个节点下标为 i,那么父亲节点的下标为 (i-1)/2
// 一个节点下标为 i,那么左儿子的下标为 2i+1,右儿子下标为 2i+2
Array []int
}
// 初始化一个堆
func NewHeap(array []int) *Heap {
h := new(Heap)
h.Array = array
return h
}
// 最大堆插入元素
func (h *Heap) Push(x int) {
// 堆没有元素时,使元素成为顶点后退出
if h.Size == 0 {
h.Array[0] = x
h.Size++
return
}
// i 是要插入节点的下标
i := h.Size
// 如果下标存在
// 将小的值 x 一直上浮
for i > 0 {
// parent为该元素父亲节点的下标
parent := (i - 1) / 2
// 如果插入的值小于等于父亲节点,那么可以直接退出循环,因为父亲仍然是最大的
if x <= h.Array[parent] {
break
}
// 否则将父亲节点与该节点互换,然后向上翻转,将最大的元素一直往上推
h.Array[i] = h.Array[parent]
i = parent
}
// 将该值 x 放在不会再翻转的位置
h.Array[i] = x
// 堆数量加一
h.Size++
}
// 最大堆移除根节点元素,也就是最大的元素
func (h *Heap) Pop() int {
// 没有元素,返回-1
if h.Size == 0 {
return -1
}
// 取出根节点
ret := h.Array[0]
// 因为根节点要被删除了,将最后一个节点放到根节点的位置上
h.Size--
x := h.Array[h.Size] // 将最后一个元素的值先拿出来
h.Array[h.Size] = ret // 将移除的元素放在最后一个元素的位置上
// 对根节点进行向下翻转,小的值 x 一直下沉,维持最大堆的特征
i := 0
for {
// a,b为下标 i 左右两个子节点的下标
a := 2*i + 1
b := 2*i + 2
// 左儿子下标超出了,表示没有左子树,那么右子树也没有,直接返回
if a >= h.Size {
break
}
// 有右子树,拿到两个子节点中较大节点的下标
if b < h.Size && h.Array[b] > h.Array[a] {
a = b
}
// 父亲节点的值都大于或等于两个儿子较大的那个,不需要向下继续翻转了,返回
if x >= h.Array[a] {
break
}
// 将较大的儿子与父亲交换,维持这个最大堆的特征
h.Array[i] = h.Array[a]
// 继续往下操作
i = a
}
// 将最后一个元素的值 x 放在不会再翻转的位置
h.Array[i] = x
return ret
}
func main() {
list := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
// 构建最大堆
h := NewHeap(list)
for _, v := range list {
h.Push(v)
}
// 将堆元素移除
for range list {
h.Pop()
}
// 打印排序后的值
fmt.Println(list)
}
运行结果:
[Running] go run "e:\golang开发学习\go_pro\test.go"
[1 3 4 5 6 6 6 8 9 14 25 49]
[Done] exited with code=0 in 1.228 seconds
2.2.5 堆排序实现
package main
import (
"fmt"
)
// 一个最大堆,一棵完全二叉树
// 最大堆要求节点元素都不小于其左右孩子
type Heap struct {
Size int // 堆的大小
// 使用内部的数组来模拟树
// 一个节点下标为 i,那么父亲节点的下标为 (i-1)/2
// 一个节点下标为 i,那么左儿子的下标为 2i+1,右儿子下标为 2i+2
Array []int
}
// 初始化一个堆
func NewHeap(array []int) *Heap {
h := new(Heap)
h.Array = array
return h
}
// 最大堆插入元素
func (h *Heap) Push(x int) {
// 堆没有元素时,使元素成为顶点后退出
if h.Size == 0 {
h.Array[0] = x
h.Size++
return
}
// i 是要插入节点的下标
i := h.Size
// 如果下标存在
// 将小的值 x 一直上浮
for i > 0 {
// parent为该元素父亲节点的下标
parent := (i - 1) / 2
// 如果插入的值小于等于父亲节点,那么可以直接退出循环,因为父亲仍然是最大的
if x <= h.Array[parent] {
break
}
// 否则将父亲节点与该节点互换,然后向上翻转,将最大的元素一直往上推
h.Array[i] = h.Array[parent]
i = parent
}
// 将该值 x 放在不会再翻转的位置
h.Array[i] = x
// 堆数量加一
h.Size++
}
// 最大堆移除根节点元素,也就是最大的元素
func (h *Heap) Pop() int {
// 没有元素,返回-1
if h.Size == 0 {
return -1
}
// 取出根节点
ret := h.Array[0]
// 因为根节点要被删除了,将最后一个节点放到根节点的位置上
h.Size--
x := h.Array[h.Size] // 将最后一个元素的值先拿出来
h.Array[h.Size] = ret // 将移除的元素放在最后一个元素的位置上
// 对根节点进行向下翻转,小的值 x 一直下沉,维持最大堆的特征
i := 0
for {
// a,b为下标 i 左右两个子节点的下标
a := 2*i + 1
b := 2*i + 2
// 左儿子下标超出了,表示没有左子树,那么右子树也没有,直接返回
if a >= h.Size {
break
}
// 有右子树,拿到两个子节点中较大节点的下标
if b < h.Size && h.Array[b] > h.Array[a] {
a = b
}
// 父亲节点的值都大于或等于两个儿子较大的那个,不需要向下继续翻转了,返回
if x >= h.Array[a] {
break
}
// 将较大的儿子与父亲交换,维持这个最大堆的特征
h.Array[i] = h.Array[a]
// 继续往下操作
i = a
}
// 将最后一个元素的值 x 放在不会再翻转的位置
h.Array[i] = x
return ret
}
// 先自底向上构建最大堆,再移除堆元素实现堆排序
func SortHeap(array []int) {
// 堆的元素数量
count := len(array)
// 最底层的叶子节点下标,该节点位置不定,但是该叶子节点右边的节点都是叶子节点
start := count/2 + 1
// 最后的元素下标
end := count - 1
// 从最底层开始,逐一对节点进行下沉
for start >= 0 {
sift(array, start, count)
start-- // 表示左偏移一个节点,如果该层没有节点了,那么表示到了上一层的最右边
}
// 下沉结束了,现在要来排序了
// 元素大于2个的最大堆才可以移除
for end > 0 {
// 将堆顶元素与堆尾元素互换,表示移除最大堆元素
array[end], array[0] = array[0], array[end]
// 对堆顶进行下沉操作
sift(array, 0, end)
// 一直移除堆顶元素
end--
}
}
// 下沉操作,需要下沉的元素时 array[start],参数 count 只要用来判断是否到底堆底,使得下沉结束
func sift(array []int, start, count int) {
// 父亲节点
root := start
// 左儿子
child := root*2 + 1
// 如果有下一代
for child < count {
// 右儿子比左儿子大,那么要翻转的儿子改为右儿子
if count-child > 1 && array[child] < array[child+1] {
child++
}
// 父亲节点比儿子小,那么将父亲和儿子位置交换
if array[root] < array[child] {
array[root], array[child] = array[child], array[root]
// 继续往下沉
root = child
child = root*2 + 1
} else {
return
}
}
}
func main() {
// list := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
// // 构建最大堆
// h := NewHeap(list)
// for _, v := range list {
// h.Push(v)
// }
// // 将堆元素移除
// for range list {
// h.Pop()
// }
// // 打印排序后的值
// fmt.Println(list)
list := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
SortHeap(list)
fmt.Println(list)
list = []int{-1, 5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
SortHeap(list)
fmt.Println(list)
list = []int{-1, 11, 22, 33}
SortHeap(list)
fmt.Println(list)
}
运行结果:
[Running] go run "e:\golang开发学习\go_pro\test.go"
[1 3 4 5 6 6 6 8 9 14 25 49]
[-1 1 3 4 5 6 6 6 8 9 14 25 49]
[-1 11 22 33]
[Done] exited with code=0 in 1.215 seconds
2.3 归并排序
2.3.1 分治法
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
分治模式在每一层递归上有三个步骤:
- 分解(Divide):将n个元素分成个含n/2个元素的子序列。
- 解决(Conquer):用合并排序法对两个子序列递归的排序。
- 合并(Combine):合并两个已排序的子序列已得到排序结果。
2.3.2 归并排序的核心思想
如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。
归并排序就是利用分治法的思想,主要分为拆和合两个阶段:
- 拆:把要排序的长度为n数组从中间开始拆分为长度为n/2的数组,然后把n/2长度的数组继续递归拆分为长度为1的子序列,最终就是长度为n的数组被拆分为n个长度为1的子序列。因为子序列的长度是1可以理解它就是有序的。
- 合:拆分完的子序列两两合并为有序列的粒度更大的子序列,经过逐级归并最终得到原数组的排序结果

2.3.3 代码实现
首先是拆分的过程,使用递归的方法将数组逐级拆分为长度为1的数组:
func mergeSort(arr []int,start ,end int) {
if start >= end {
return
}
mid := (start+end)/2
//从中间位置拆分数组
mergeSort(arr,start,mid)
mergeSort(arr,mid + 1,end)
//将拆分后的数组进行合并
merge(arr,start,mid,end)
}
其次是合并:
func merge(arr []int,start,mid,end int){
rightIndex := start
leftIndex := mid + 1
tmpIndex := 0
tmp := make([]int,1 + end - start)
//取两个子序列较小元素放入tmp
for rightIndex <= mid && leftIndex <= end {
if arr[rightIndex] <= arr[leftIndex] {
tmp[tmpIndex] = arr[rightIndex]
tmpIndex++
rightIndex++
}else {
tmp[tmpIndex] = arr[leftIndex]
tmpIndex++
leftIndex++
}
}
//判断是哪边的序列还有剩余元素
var appendStart,appendEnd int
if rightIndex > mid {
appendStart = leftIndex
appendEnd = end
}else {
appendStart = rightIndex
appendEnd = mid
}
//将剩余元素放入tmp
for appendStart <= appendEnd {
tmp[tmpIndex] = arr[appendStart]
tmpIndex++
appendStart++
}
//将tmp中元素放入原数组
for k,v :=range tmp{
arr[start + k] = v
}
}
func merge(arr []int,start,mid,end int)具体代码里声明了一个tmp用于存储左侧元素和右侧元素的排序结果。从左右两测子序列的头部偏移量为0开始遍历比较,取最小的元素放入tmp中并且将这个子序列的偏移量+1。直到其中一个子序列的元素都被放在了tmp中,就可以把另一个子序列的剩余元素直接放入tmp中。
测试:
package main
import "fmt"
func mergeSort(arr []int, start, end int) {
if start >= end {
return
}
mid := (start + end) / 2
//从中间位置拆分数组
mergeSort(arr, start, mid)
mergeSort(arr, mid+1, end)
//将拆分后的数组进行合并
merge(arr, start, mid, end)
}
func merge(arr []int, start, mid, end int) {
rightIndex := start
leftIndex := mid + 1
tmpIndex := 0
tmp := make([]int, 1+end-start)
//取两个子序列较小元素放入tmp
for rightIndex <= mid && leftIndex <= end {
if arr[rightIndex] <= arr[leftIndex] {
tmp[tmpIndex] = arr[rightIndex]
tmpIndex++
rightIndex++
} else {
tmp[tmpIndex] = arr[leftIndex]
tmpIndex++
leftIndex++
}
}
//判断是哪边的序列还有剩余元素
var appendStart, appendEnd int
if rightIndex > mid {
appendStart = leftIndex
appendEnd = end
} else {
appendStart = rightIndex
appendEnd = mid
}
//将剩余元素放入tmp
for appendStart <= appendEnd {
tmp[tmpIndex] = arr[appendStart]
tmpIndex++
appendStart++
}
//将tmp中元素放入原数组
for k, v := range tmp {
arr[start+k] = v
}
}
func main() {
arr := []int{1, 2, 3, 1, 5, 3, 2, 1, 4, 6, 9, 7}
mergeSort(arr, 0, len(arr)-1)
fmt.Println(arr)
}
运行结果:
[Running] go run "e:\golang开发学习\go_pro\test.go"
[1 1 1 2 2 3 3 4 5 6 7 9]
[Done] exited with code=0 in 1.208 seconds
三 其他排序法归并排序的时间复杂度非常稳定在任何情况都是O(nlogn),单从时间复杂度来考虑的话是一种非常优秀的排序方法,但是归并排序的空间复杂度却不像插入排序、快速排序一样,它的空间复杂度是O(n),所以在应用上并不是非常广泛。
3.1 希尔排序
希尔排序是直接插入排序的改进版本。因为直接插入排序对那些几乎已经排好序的数列来说,排序效率极高,达到了 O(n) 的线性复杂度,但是每次只能将数据移动一位。希尔排序创造性的可以将数据移动 n 位,然后将 n 一直缩小,缩到与直接插入排序一样为 1。
排序思想:
有一个 N 个数的数列:
- 先取一个小于 N 的整数 d1,将位置是 d1 整数倍的数们分成一组,对这些数进行直接插入排序。
- 接着取一个小于 d1 的整数 d2,将位置是 d2 整数倍的数们分成一组,对这些数进行直接插入排序。
- 接着取一个小于 d2 的整数 d3,将位置是 d3 整数倍的数们分成一组,对这些数进行直接插入排序。
- …
- 直到取到的整数 d=1,接着使用直接插入排序。
举个简单例子,希尔排序一个 12 个元素的数列:[5 9 1 6 8 14 6 49 25 4 6 3],增量 d 的取值依次为:6,3,1:
- 取 d = 6 对 [5 x x x x x 6 x x x x x] 进行直接插入排序
没有变化。 - 取 d = 3 对 [5 x x 6 x x 6 x x 4 x x] 进行直接插入排序
排完序后:[4 x x 5 x x 6 x x 6 x x]。 - 取 d = 1 对 [4 9 1 5 8 14 6 49 25 6 6 3] 进行直接插入排序
因为 d=1 完全就是直接插入排序了。
代码实现:
package main
import "fmt"
// 增量序列折半的希尔排序
func SortShell(list []int) {
// 数组长度
n := len(list)
// 每次减半,直到步长为 1
for step := n / 2; step >= 1; step /= 2 {
// 开始插入排序,每一轮的步长为 step
for i := step; i < n; i += step {
for j := i - step; j >= 0; j -= step {
// 满足插入那么交换元素
if list[j+step] < list[j] {
list[j], list[j+step] = list[j+step], list[j]
continue
}
break
}
}
}
}
func main() {
list := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
SortShell(list)
fmt.Println(list)
list = []int{-1, 5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
SortShell(list)
fmt.Println(list)
list = []int{-1, 11, 22, 33}
SortShell(list)
fmt.Println(list)
}
运行结果:
[Running] go run "e:\golang开发学习\go_pro\test.go"
[1 3 4 5 6 6 6 8 9 14 25 49]
[-1 1 3 4 5 6 6 6 8 9 14 25 49]
[-1 11 22 33]
[Done] exited with code=0 in 1.058 seconds
3.2 计数排序
计数排序(Counting sort) 是一种稳定的线性时间排序算法.计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。计数排序使用一个额外的数组C,其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C 来将A中的元素排到正确的位置。
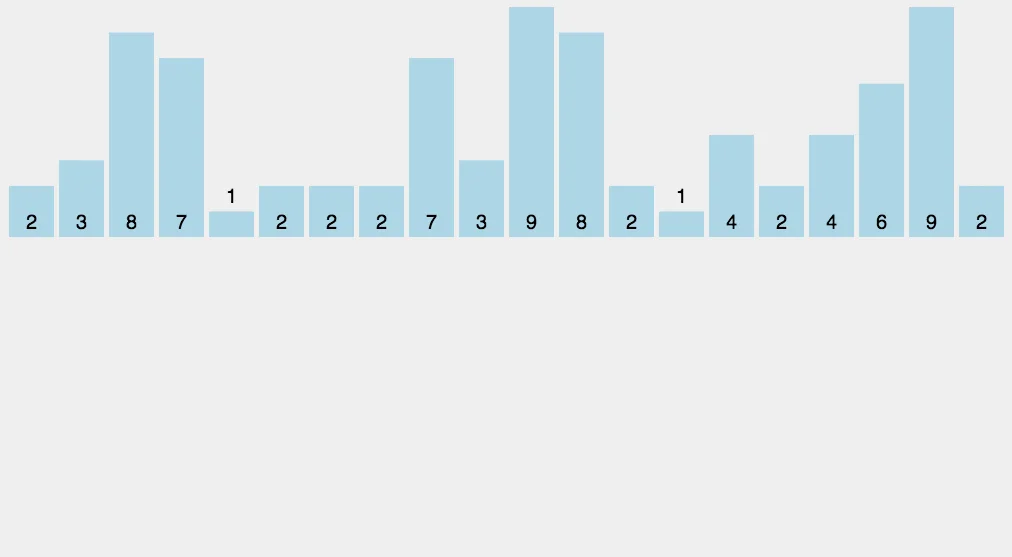
排序思路:
- 找出待排序的数组中最大和最小的元素.
- 统计数组中每个值为i的元素出现的次数,存入数组C的第i项.
- 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加).
- 反向填充目标数组:将每个元素 i放在新数组的第C[i]项,每放一个元素就将C[i]减去1.
代码实现:
package main
import (
"fmt"
"math/rand"
"time"
)
// 计数排序--升序
func ContingSortAsc(slice []int) {
// 创建map统计0-999每个数出现的次数
m := make(map[int]int)
// 遍历待排序的数据,统计结果
for _, v := range slice {
m[v]++
}
// 借助map,统计排序的数据重新赋值为原序列
slice = slice[0:0] // 将原序列清空
for i := 0; i < 1000; i++ {
// for i := 0; i < 1000; i++ {
// 数据出现的次数:m[i]的值
for j := 0; j < m[i]; j++ {
slice = append(slice, i) // 重新赋值
}
}
}
// 计数排序--降序
func ContingSortDesc(slice []int) {
// 创建map统计0-999每个数出现的次数
m := make(map[int]int)
// 遍历待排序的数据,统计结果
for _, v := range slice {
m[v]++
}
// 借助map,统计排序的数据重新赋值为原序列
slice = slice[0:0] // 将原序列清空
for i := 999; i >= 0; i-- {
// for i := 0; i < 1000; i++ {
// 数据出现的次数:m[i]的值
for j := 0; j < m[i]; j++ {
slice = append(slice, i) // 重新赋值
}
}
}
func main() {
slice := make([]int, 0)
// 设置随机数种子
rand.Seed(time.Now().UnixNano())
// 生成100个1000以内的随机数
for i := 1; i <= 100; i++ {
slice = append(slice, rand.Intn(1000))
}
fmt.Println("原数据:", slice)
ContingSortAsc(slice)
fmt.Println("计数排序升序:", slice)
ContingSortDesc(slice)
fmt.Println("计数排序降序:", slice)
}
运行结果:
[Running] go run "e:\golang开发学习\go_pro\test.go"
原数据: [387 575 55 143 11 33 402 496 570 123 180 74 68 230 967 974 217 375 651 292 698 986 841 524 335 37 280 464 893 695 81 348 437 444 828 554 639 127 888 503 902 656 822 103 214 328 583 118 205 776 106 141 979 531 290 73 214 8 899 470 607 93 489 490 626 848 439 766 130 936 488 362 518 365 568 492 449 864 484 933 2 870 465 746 399 880 322 194 394 642 955 714 431 57 668 792 273 813 781 748]
计数排序升序: [2 8 11 33 37 55 57 68 73 74 81 93 103 106 118 123 127 130 141 143 180 194 205 214 214 217 230 273 280 290 292 322 328 335 348 362 365 375 387 394 399 402 431 437 439 444 449 464 465 470 484 488 489 490 492 496 503 518 524 531 554 568 570 575 583 607 626 639 642 651 656 668 695 698 714 746 748 766 776 781 792 813 822 828 841 848 864 870 880 888 893 899 902 933 936 955 967 974 979 986]
计数排序降序: [986 979 974 967 955 936 933 902 899 893 888 880 870 864 848 841 828 822 813 792 781 776 766 748 746 714 698 695 668 656 651 642 639 626 607 583 575 570 568 554 531 524 518 503 496 492 490 489 488 484 470 465 464 449 444 439 437 431 402 399 394 387 375 365 362 348 335 328 322 292 290 280 273 230 217 214 214 205 194 180 143 141 130 127 123 118 106 103 93 81 74 73 68 57 55 37 33 11 8 2]
[Done] exited with code=0 in 1.551 seconds
3.3 桶排序
排序思想:
基数排序
代码实现:
package main
import(
"fmt"
"math/rand"
"time"
)
func Bucket_Sort(arr []int, n int, max_num int){
// 二维切片初始化 先给一个行数
var buckets [][]int = make([][]int, n)
for _, val := range arr{
p := val / (max_num / n)
if p > n -1 {
// 把 最大 10000 放到 99号桶
p = n - 1
}
buckets[p] = append(buckets[p], val)
// 赋值后即排序
for k := len(buckets[p]) - 1; k > 0; k-- {
// 桶内冒泡排序
if buckets[p][k] < buckets[p][k - 1]{
buckets[p][k], buckets[p][k - 1] = buckets[p][k - 1], buckets[p][k]
}else{
break
}
}
// 输出桶内元素
// 清空切片
arr = arr[0:0]
for i := 0; i < n; i++ {
arr = append(arr, buckets[i]...)
}
}
}
// 生成随机int切片 正整数 rand.Intn返回一个非负伪随机数[0,n)作为int。如果n <= 0则报错
func rand_array(arr []int, min int, max int){
if min >= max || min == 0 || max == 0{
fmt.Println("输入最大, 最小值有误!")
return
}
// 如果不加这个 每次会生成一样的
rand.Seed(time.Now().Unix())
for i := 0; i < len(arr); i++{
arr[i] = rand.Intn(max - min) + min
}
}
func main(){
min := 100
max := 10000
var mylist []int = make([]int, 100)
rand_array(mylist, min, max)
fmt.Printf("随机的int 切片为:%d\n", mylist)
Bucket_Sort(mylist, 100, 10000)
fmt.Printf("桶排序排序后的int 切片为:%d\n", mylist)
}
运行结果:
[Running] go run "e:\golang开发学习\go_pro\test.go"
随机的int 切片为:[2393 2423 4286 191 6869 1858 963 9148 7177 2343 8558 8167 3025 5492 1599 9012 6245 9551 2364 732 5439 7909 447 8678 4093 4707 3789 8682 9582 1590 883 1756 7030 1210 6783 8691 1444 2144 5717 2468 7648 6032 3209 4909 1730 6429 2938 101 2504 4323 1133 9364 5258 5050 7512 8383 2999 3648 2138 7906 4215 2346 9269 4305 5059 699 1558 1856 3990 1829 2591 1235 8582 3381 7524 1829 8599 197 2897 2523 678 3203 3960 8955 8225 4781 4304 9402 9951 9014 6771 145 8572 8409 2475 8205 9027 1329 7647 6954]
桶排序排序后的int 切片为:[101 145 191 197 447 678 699 732 883 963 1133 1210 1235 1329 1444 1558 1590 1599 1730 1756 1829 1829 1856 1858 2138 2144 2343 2346 2364 2393 2423 2468 2475 2504 2523 2591 2897 2938 2999 3025 3203 3209 3381 3648 3789 3960 3990 4093 4215 4286 4304 4305 4323 4707 4781 4909 5050 5059 5258 5439 5492 5717 6032 6245 6429 6771 6783 6869 6954 7030 7177 7512 7524 7647 7648 7906 7909 8167 8205 8225 8383 8409 8558 8572 8582 8599 8678 8682 8691 8955 9012 9014 9027 9148 9269 9364 9402 9551 9582 9951]
[Done] exited with code=0 in 1.052 seconds
3.4 基数排序
排序思想:
- 先以个位数的大小对数据进行排序
- 接着以十位数的大小对数据进行排序
- 接着以百位数…
- 排到最后,就是一组有序数列了
基数排序在以某位数进行排序的时候,是以“桶”来排序的。
由于某位数(个/十…,不是整个数)的大小范围为0-9,所以我们需要10个桶,然后把具有相同数值的数放进同一个桶内,之后再把桶里的数按照0号桶-9号桶的顺序取出来,这样一趟下来,按照某位数的排序就完成了

代码实现:
package main
import "fmt"
// 基数排序
func BaseSort(data []int) []int {
if len(data) < 2 {
return data
}
max := data[0]
dataLen := len(data)
for i := 1; i < dataLen; i++ {
if data[i] > max {
max = data[i]
}
}
// 计算最大值的位数
maxDigit := 0
for max > 0 {
max = max / 10
maxDigit++
}
// 定义每一轮的除数,1,10,100...
divisor := 1
// 定义了10个桶,为了防止每一位都一样所以将每个桶的长度设为最大,与原数组大小相同
bucket := [10][20]int{{0}}
// 统计每个桶中实际存放的元素个数
count := [10]int{0}
// 获取元素中对应位上的数字,即装入那个桶
var digit int
// 经过maxDigit+1次装通操作,排序完成
for i := 1; i <= maxDigit; i++ {
for j := 0; j < dataLen; j++ {
tmp := data[j]
digit = (tmp / divisor) % 10
bucket[digit][count[digit]] = tmp
count[digit]++
}
// 被排序数组的下标
k := 0
// 从0到9号桶按照顺序取出
for b := 0; b < 10; b++ {
if count[b] == 0 {
continue
}
for c := 0; c < count[b]; c++ {
data[k] = bucket[b][c]
k++
}
count[b] = 0
}
divisor = divisor * 10
}
return data
}
func main() {
a := []int{19, 2, 415, 5, 0}
BaseSort(a)
fmt.Println(a)
}
运行结果:
[Running] go run "e:\golang开发学习\go_pro\test.go"
[0 2 5 19 415]
[Done] exited with code=0 in 1.152 seconds
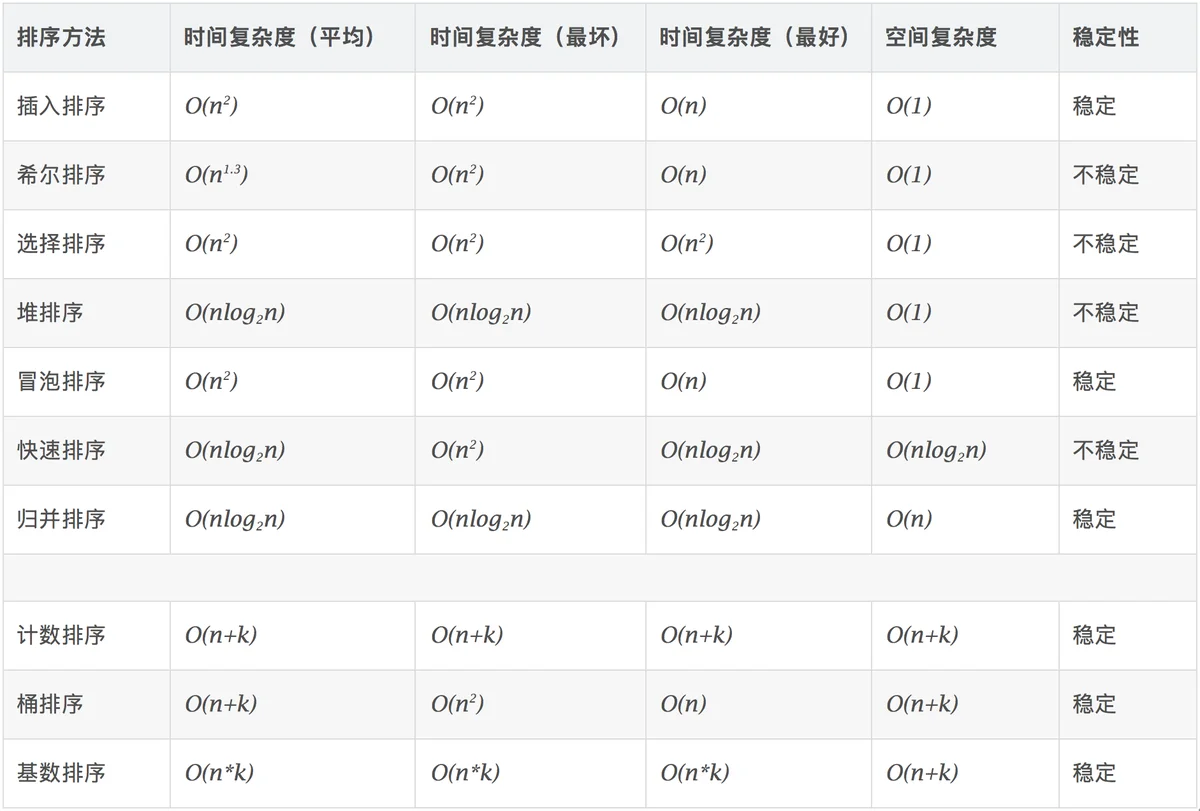
相关概念:
- 稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
- 不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
- 时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
- 空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
