从前序与中序遍历序列构造二叉树 golang

105 从前序与中序遍历序列构造二叉树

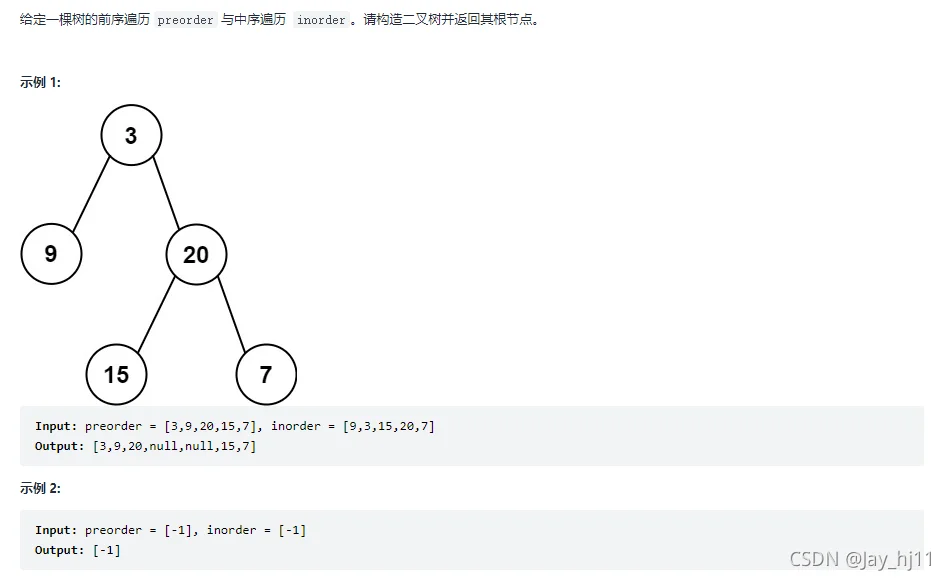
方法一：递归
思路
对于任意一颗树而言，前序遍历的形式是

[ 根, [左子树的前序遍历结果], [右子树的前序遍历结果] ]

即根节点总是前序遍历中的第一个节点。
而中序遍历的形式是

[ [左子树的中序遍历结果], 根, [右子树的中序遍历结果] ]

只要我们在中序遍历中定位到根节点，那么我们就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的，因此我们就可以对应到前序遍历的结果中，对上述形式中的所有左右括号进行定位。

下面是代码实现：

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func buildTree(preorder []int, inorder []int) *TreeNode {
    if len(preorder) ==0 || len(inorder)==0{
        return nil
    }
    root :=&TreeNode{preorder[0],nil,nil}
    i :=0
    for ;i<len(inorder);i++{
        if inorder[i]==preorder[0]{
            break
        }
    }
    //关于这里为什么是i+1,而不是i 或者i+2的原因
    //https://blog.csdn.net/Jason_hj11/article/details/121425326?spm=1001.2014.3001.5501 切片截取时，不包括后面的索引
    root.Left = buildTree(preorder[1:i+1],inorder[:i])
    root.Right = buildTree(preorder[i+1:],inorder[i+1:])
    return root
}

优化思路：
这里传的如果是节点数组而不是int数组，我们可以做一个字典map，就不用每次去loop找根节点index。

还有迭代法去解决这问题，详见官方解答。