12484c445a4537bac41baa0b18a80510.png

该系列题目取自 LeetCode 精选 TOP 面试题列表：https://leetcode-cn.com/problemset/top/

题目描述

原题链接：https://leetcode-cn.com/problems/maximum-depth-of-binary-tree

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明：叶子节点是指没有子节点的节点。

示例：

[3,9,20,null,null,15,7]
    3
   / \
  9  20
    /  \
   15   7

返回它的最大深度 3 。

解题思路

题目要求求出二叉树的最大深度，我们知道，每个节点的深度与它左右子树的深度有关，且等于其左右子树最大深度值加上 1，可以写作：

maxDepth(root) = max(maxDepth(root.left), maxDepth(root.right)) + 1
[3,9,20,null,null,15,7]3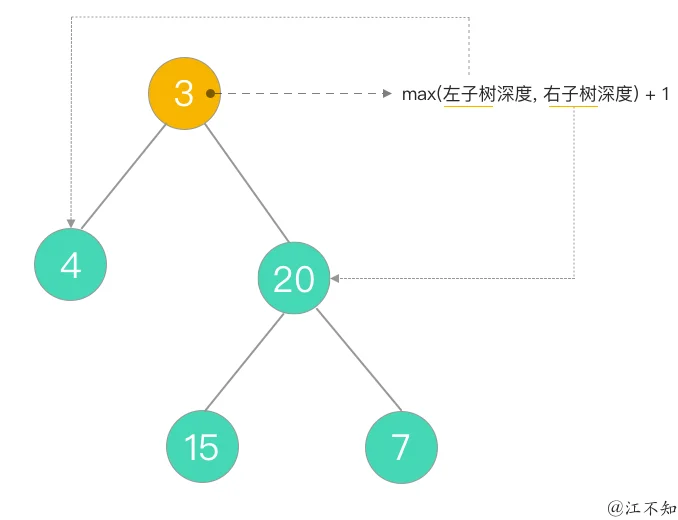
a8040b5edd18da8decd4d12f3f702ace.png

因其左右子树深度尚不可知，我们需要对其一一求解。

4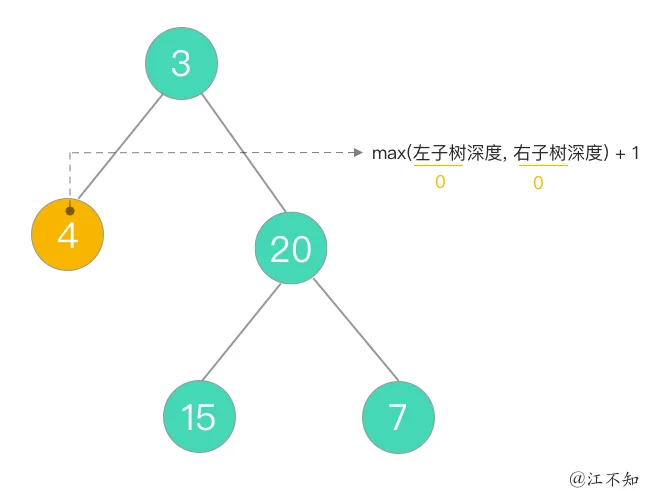
562c132ca77c075b09d2bdd97738c320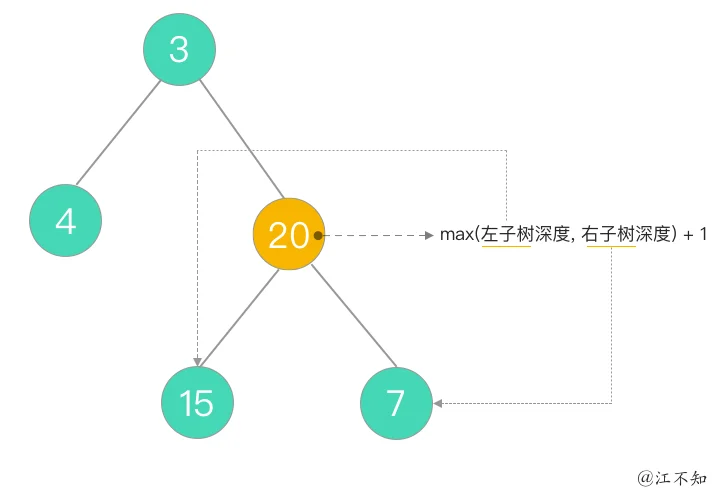.png 
20
8d5cce14ec96b12e679f8e593d335e88.png 
157420
max(左子树最大深度, 右子树最大深度) + 1
=
max(1, 1) + 1
=
1 + 1
=
2

这样一来，我们知道了所有子节点的深度，各节点深度如下：

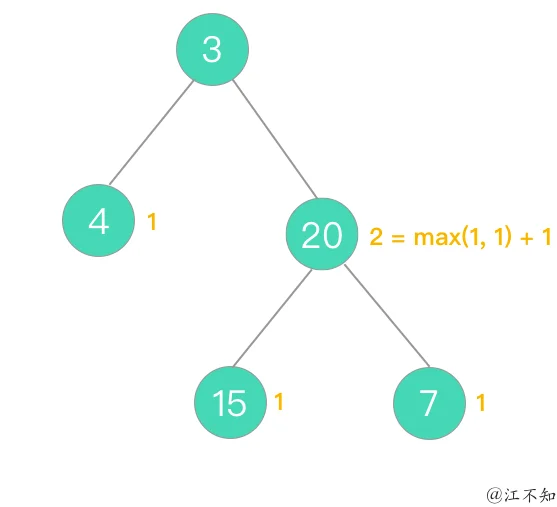
a91d77afaf1903ee3f7125994e1b3e8e.png

由此可得根节点 3 的深度为：

max(左子树最大深度, 右子树最大深度) + 1
=
max(1, 2) + 1
=
2 + 1
=
3

上述推导过程整体如下：

maxDepth(3-root)
=
max(maxDepth(4-sub), maxDepth(20-sub)) + 1
=
max(1, max(maxDepth(15-sub), maxDepth(7-sub)) + 1) + 1
=
max(1, maxDepth(1, 1) + 1) + 1
=
max(1, 2) + 1
=
2 + 1
=
3
maxDepth()

递归设计

在递归算法中，递归函数的设计非常重要，首先我们要先明确该函数的作用，然后再确定何时结束与何时调用该函数。

明确函数作用

该函数的作用用一句话概括就是：计算节点的最大深度。

  • 函数输入：确定的节点
  • 函数输出：该节点的最大深度

何时结束

当输入的节点为空节点时，我们无需继续计算其子树的深度，此时可以直接结束递归函数，并返回空节点的深度为 0。

何时调用

当输入节点为非空节点时，该节点的深度取决于其左右子树的深度，即：

maxDepth(root) = max(maxDepth(root.left), maxDepth(root.right)) + 1

此时需要进行函数的递归调用。

具体实现

Python

# Definition for a binary tree node.

Golang

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */

复杂度

假设节点的数量为 n。

时间复杂度

O(n)

空间复杂度

考虑到递归使用调用栈(call stack)的情况。

O(n)log(n)O(log(n))

总结一下

与树相关的题目常用递归来解，对于递归而言，我们需要明确：

  1. 递归函数的用途
  2. 递归函数的结束条件
  3. 递归函数自身调用的时机

除此之外，在计算空间复杂度时，我们也要考虑到递归时调用栈的情况。

当然了，这道题还可以用迭代法来做，由于篇幅有限，就不在本篇叙述了。大家可以想想要怎么用迭代法解答本题，我们下次再来细说~

其他二叉树相关

  • 详解算法之重建二叉树

  • 二叉树的后序遍历(非递归版)

  • 二叉树的先序遍历(非递归版)

  • 二叉树的中序遍历(非递归版)

  • 从上往下打印二叉树

  • 二叉搜索树的后序遍历序列

  • 剑指offer：二叉树镜像

  • 剑指offer：二叉树的子结构

  • 剑指offer：重建二叉树

12484c445a4537bac41baa0b18a80510.png