
目录
221. 最大正方形 Maximal Square
'0''1''1'示例 1:
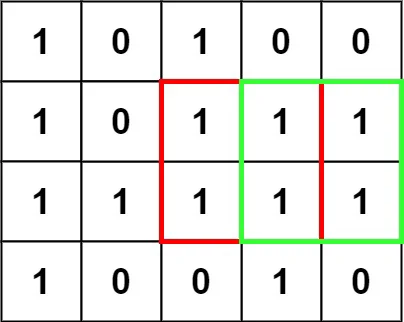
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]] 输出:4
示例 2:
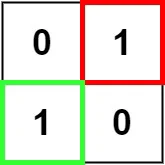
输入:matrix = [["0","1"],["1","0"]] 输出:1
示例 3:
输入:matrix = [["0"]] 输出:0
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 300matrix[i][j]'0''1'代码1: 暴力枚举
package main
import (
"fmt"
)
func maximalSquare(matrix [][]byte) int {
m, n := len(matrix), len(matrix[0])
maxLen := 0
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
if matrix[i][j] == '1' {
curLen := 1
flag := true
for k := 1; k+i < m && k+j < n && flag; k++ {
for l := 0; l <= k; l++ {
if matrix[i+k][j+l] == '0' || matrix[i+l][j+k] == '0' {
flag = false
break
}
}
if flag {
curLen++
}
}
if curLen > maxLen {
maxLen = curLen
}
}
}
}
return maxLen * maxLen
}
func main() {
matrix := [][]byte{{'1', '0', '1', '0', '0'}, {'1', '0', '1', '1', '1'}, {'1', '1', '1', '1', '1'}, {'1', '0', '0', '1', '0'}}
fmt.Println(maximalSquare(matrix))
matrix = [][]byte{{'0', '1'}, {'1', '0'}}
fmt.Println(maximalSquare(matrix))
matrix = [][]byte{{'0'}}
fmt.Println(maximalSquare(matrix))
}
代码2: 动态规划
package main
import (
"fmt"
)
func maximalSquare(matrix [][]byte) int {
m, n := len(matrix), len(matrix[0])
maxLen := 0
dp := make([][]int, m)
for i := 0; i < m; i++ {
dp[i] = make([]int, n)
for j := 0; j < n; j++ {
if matrix[i][j] == '1' {
if i == 0 || j == 0 {
dp[i][j] = 1
} else {
dp[i][j] = min(dp[i-1][j], min(dp[i][j-1], dp[i-1][j-1])) + 1
}
if dp[i][j] > maxLen {
maxLen = dp[i][j]
}
}
}
}
return maxLen * maxLen
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
func main() {
matrix := [][]byte{{'1', '0', '1', '0', '0'}, {'1', '0', '1', '1', '1'}, {'1', '1', '1', '1', '1'}, {'1', '0', '0', '1', '0'}}
fmt.Println(maximalSquare(matrix))
matrix = [][]byte{{'0', '1'}, {'1', '0'}}
fmt.Println(maximalSquare(matrix))
matrix = [][]byte{{'0'}}
fmt.Println(maximalSquare(matrix))
}
代码3: 动态规划优化
package main
import (
"fmt"
)
func maximalSquare(matrix [][]byte) int {
m, n := len(matrix), len(matrix[0])
maxLen := 0
cur := make([]int, n)
pre := make([]int, n)
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
if matrix[i][j] == '1' {
if i == 0 || j == 0 {
cur[j] = 1
} else {
cur[j] = min(pre[j], min(cur[j-1], pre[j-1])) + 1
}
if cur[j] > maxLen {
maxLen = cur[j]
}
} else {
cur[j] = 0
}
}
cur, pre = pre, cur
}
return maxLen * maxLen
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
func main() {
matrix := [][]byte{{'1', '0', '1', '0', '0'}, {'1', '0', '1', '1', '1'}, {'1', '1', '1', '1', '1'}, {'1', '0', '0', '1', '0'}}
fmt.Println(maximalSquare(matrix))
matrix = [][]byte{{'0', '1'}, {'1', '0'}}
fmt.Println(maximalSquare(matrix))
matrix = [][]byte{{'0'}}
fmt.Println(maximalSquare(matrix))
}
输出:
4
1
0
222. 完全二叉树的节点个数 Count Complete Tree Nodes
rooth1~2^h示例 1:
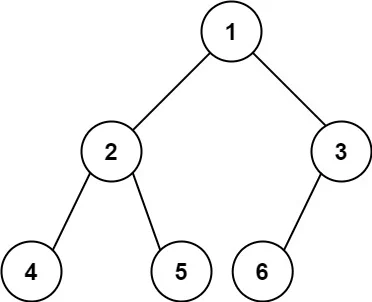
输入:root = [1,2,3,4,5,6] 输出:6
示例 2:
输入:root = [] 输出:0
示例 3:
输入:root = [1] 输出:1
提示:
[0, 5 * 10^4]0 <= Node.val <= 5 * 10^4O(n)代码1: dfs
完全二叉树,可以通过比较根节点左子树高度和右子树高度来确定它是否可以被视为完全二叉树。如果左右高度相等,则该树是满二叉树,节点个数为 2ℎ−12h−1;否则,该树可以被分成一棵满二叉树和一颗子树,递归计算子树的节点数
package main
import "fmt"
const null = -1 << 31
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func countNodes(root *TreeNode) int {
if root == nil {
return 0
}
var left, right uint
left, right = 0, 0
for node := root; node != nil; node = node.Left {
left++
}
for node := root; node != nil; node = node.Right {
right++
}
if left == right {
return (1 << left) - 1
} else {
return countNodes(root.Left) + countNodes(root.Right) + 1
}
}
func buildTree(nums []int) *TreeNode {
if len(nums) == 0 {
return nil
}
root := &TreeNode{Val: nums[0]}
Queue := []*TreeNode{root}
idx := 1
for idx < len(nums) {
node := Queue[0]
Queue = Queue[1:]
if nums[idx] != null {
node.Left = &TreeNode{Val: nums[idx]}
Queue = append(Queue, node.Left)
}
idx++
if idx < len(nums) && nums[idx] != null {
node.Right = &TreeNode{Val: nums[idx]}
Queue = append(Queue, node.Right)
}
idx++
}
return root
}
func main() {
nums := []int{1, 2, 3, 4, 5, 6}
root := buildTree(nums)
fmt.Println(countNodes(root))
nums = []int{}
root = buildTree(nums)
fmt.Println(countNodes(root))
nums = []int{1}
root = buildTree(nums)
fmt.Println(countNodes(root))
}
<<代码2:bfs
将根节点放入队列中,然后对于队列中的每一个节点,将它的左右子节点入队,统计队列的大小即为节点个数
package main
import "fmt"
const null = -1 << 31
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func countNodes(root *TreeNode) int {
if root == nil {
return 0
}
q := []*TreeNode{root}
count := 0
for len(q) > 0 {
size := len(q)
count += size
for i := 0; i < size; i++ {
node := q[i]
if node.Left != nil {
q = append(q, node.Left)
}
if node.Right != nil {
q = append(q, node.Right)
}
}
q = q[size:]
}
return count
}
func buildTree(nums []int) *TreeNode {
if len(nums) == 0 {
return nil
}
root := &TreeNode{Val: nums[0]}
Queue := []*TreeNode{root}
idx := 1
for idx < len(nums) {
node := Queue[0]
Queue = Queue[1:]
if nums[idx] != null {
node.Left = &TreeNode{Val: nums[idx]}
Queue = append(Queue, node.Left)
}
idx++
if idx < len(nums) && nums[idx] != null {
node.Right = &TreeNode{Val: nums[idx]}
Queue = append(Queue, node.Right)
}
idx++
}
return root
}
func main() {
nums := []int{1, 2, 3, 4, 5, 6}
root := buildTree(nums)
fmt.Println(countNodes(root))
nums = []int{}
root = buildTree(nums)
fmt.Println(countNodes(root))
nums = []int{1}
root = buildTree(nums)
fmt.Println(countNodes(root))
}
代码3:二分法
package main
import "fmt"
const null = -1 << 31
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func countNodes(root *TreeNode) int {
if root == nil {
return 0
}
left, right := countHeight(root.Left), countHeight(root.Right)
if left == right {
return (1 << left) + countNodes(root.Right)
} else {
return (1 << right) + countNodes(root.Left)
}
}
func countHeight(root *TreeNode) uint {
if root == nil {
return 0
}
return countHeight(root.Left) + 1
}
func buildTree(nums []int) *TreeNode {
if len(nums) == 0 {
return nil
}
root := &TreeNode{Val: nums[0]}
Queue := []*TreeNode{root}
idx := 1
for idx < len(nums) {
node := Queue[0]
Queue = Queue[1:]
if nums[idx] != null {
node.Left = &TreeNode{Val: nums[idx]}
Queue = append(Queue, node.Left)
}
idx++
if idx < len(nums) && nums[idx] != null {
node.Right = &TreeNode{Val: nums[idx]}
Queue = append(Queue, node.Right)
}
idx++
}
return root
}
func main() {
nums := []int{1, 2, 3, 4, 5, 6}
root := buildTree(nums)
fmt.Println(countNodes(root))
nums = []int{}
root = buildTree(nums)
fmt.Println(countNodes(root))
nums = []int{1}
root = buildTree(nums)
fmt.Println(countNodes(root))
}
输出:
6
0
1
✨ 持续,努力奋斗做强刷题搬运工!
👍 点赞,你的认可是我坚持的动力!
🌟 收藏,你的青睐是我努力的方向!
✎ 评论,你的意见是我进步的财富!
|
| (2023.5.16~)更新中... |
|
| (2023.3.11~)更新中... |
|
| (2023.2.18~2023.5.18)暂停更 |
|
| (2023.2.18~2023.5.18)暂停更 |
|
| (2023.3.11~2023.5.18)暂停更 |





