在上一篇博客《go语言｜数据结构：二叉树可视化（制作svg格式树形图）》中，已实现了用svg图片展示二叉树的树形结构。但对非满二叉树的比较复杂，需要先转成满二叉树，再获取各结点在满二叉树中的对应坐标位置，这种做法明显有个缺点就是遍历的次数比较多。
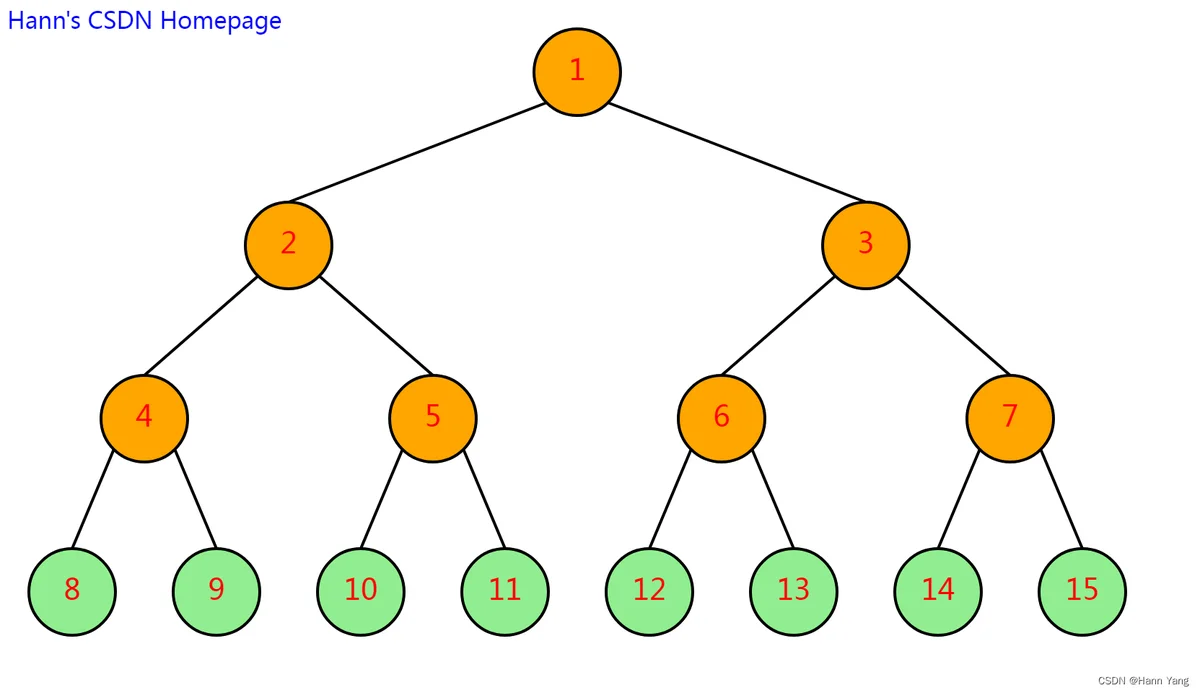
树形图的关键在于获取结点的坐标。对满二叉树的来说，它的坐标数组可以标记为：[[(0,0)], [(1,0), (1,1)], [(2,0), (2,1), (2,2), (2,3)], [(3,0),(3,1), ...], ...]；如能对任意二叉树只做一次遍布，就获得这样的坐标，效率就提高了。首先，从递归遍历说起——
递归遍历
递归遍历时，看数据域和左右子树结点出现的位置顺序看，分先序、中序、后序三种方式。不管哪种方式都可以用2种方法，一种是直接打印遍历结果、一种返回遍历结果（结点的数据域数组）。如下代码，以先序遍历为例：
创建函数Build()也作了改进，直接用变长参数，而非之前用数组作参数。另外，参数中如有不能连接的结点，直接放弃而非抛出错误panic()。如参数 1,nil,nil,2,3 就只返回一个结点。
深度的遍历
递归遍历核心就以下三行代码，先读出数据域，后左右递归的即先序遍历；读出放中间或最后一行就变成中序和后序遍历了。
如果把bt.Data换成其它呢，结点结构就定义了三个值，换成bt.Lchild，bt.Rchild就能遍历出左右子树结点。这样用处不大， 如果写成 bt.Lchild!=nil 或者 bt.Rchild!=nil，遍历结果就是该结点是否有左子树或右子树；写成 bt.Lchild==nil && bt.Rchild==nil 就能判断是否为叶结点。如果换作一个自定义函数呢，那就能得到自己想要的结果。也可以玩其它花样，比如累加所有结点的和，为了方便默认它们的数据域都是整数：
深度和高度的概念
深度是从根节点数到它的叶节点，高度是从叶节点数到它的根节点。即深度是从上到下计数的，而高度是从下往上计数。
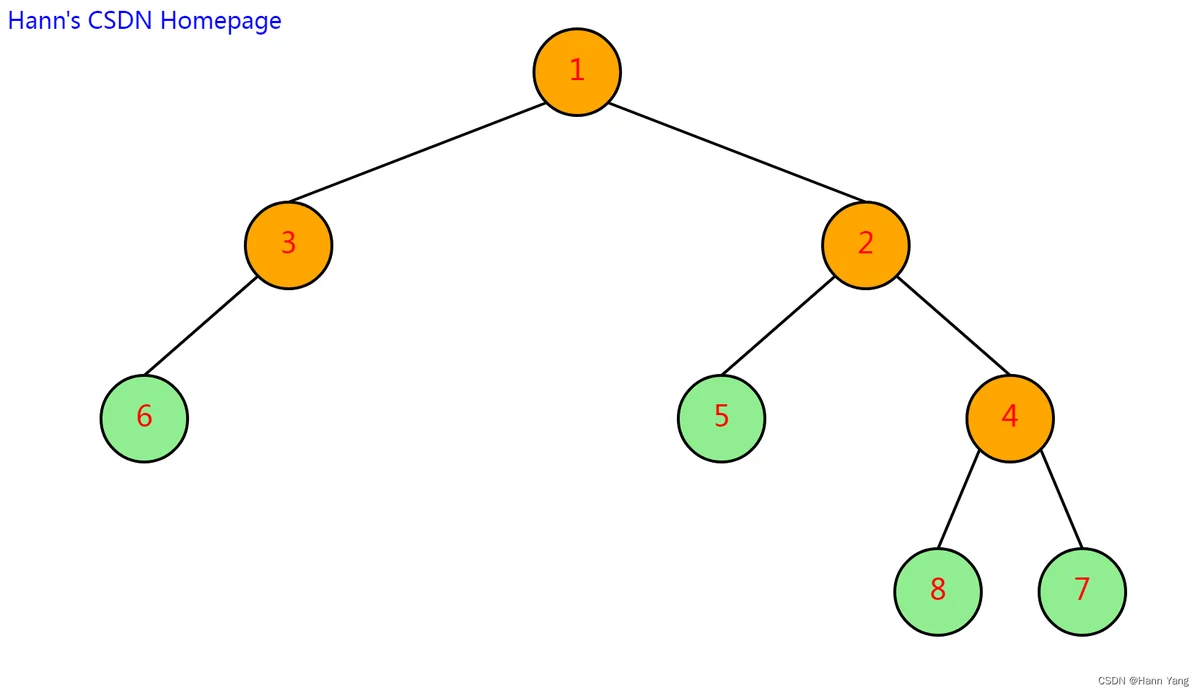
二叉树的深度是指所有结点中最深的结点所在的层数。对于整棵树来说，最深的叶结点的深度就是树的深度，即树的高度和深度是相等的。但同一层的节点的深度是相同，它们的高度不一定相同。如下图，节点2和3的深度相等，但高度不相等；节点4、5、6深度也相等，但高度不全相等。
深度的遍历
从二叉树深度的定义可知，二叉树的深度应为其左、右子树深度的最大值加1。由此，需先分别求得左、右子树的深度，算法中“访问结点”的操作为：求得左、右子树深度的最大值，然后加 1 。递归代码如下：
遍历时用上这个函数就可得到所有结点的深度了，完整测试代码以8个结点的完全二叉树为例，返回结果是：“4 3 2 1 1 2 1 1”。最大值4为根结点的尝试，也就是整个二叉树的深度或高度；四个最小值1，表示有四个叶结点。
叶结点的遍历
结点结构的三变量都用过了，对得到结点的坐标帮助不大，坐标需要的是结点在树中的层数和所在层数的索引号。于是尝试引入其它变量——
坐标的遍历
纵坐标遍历
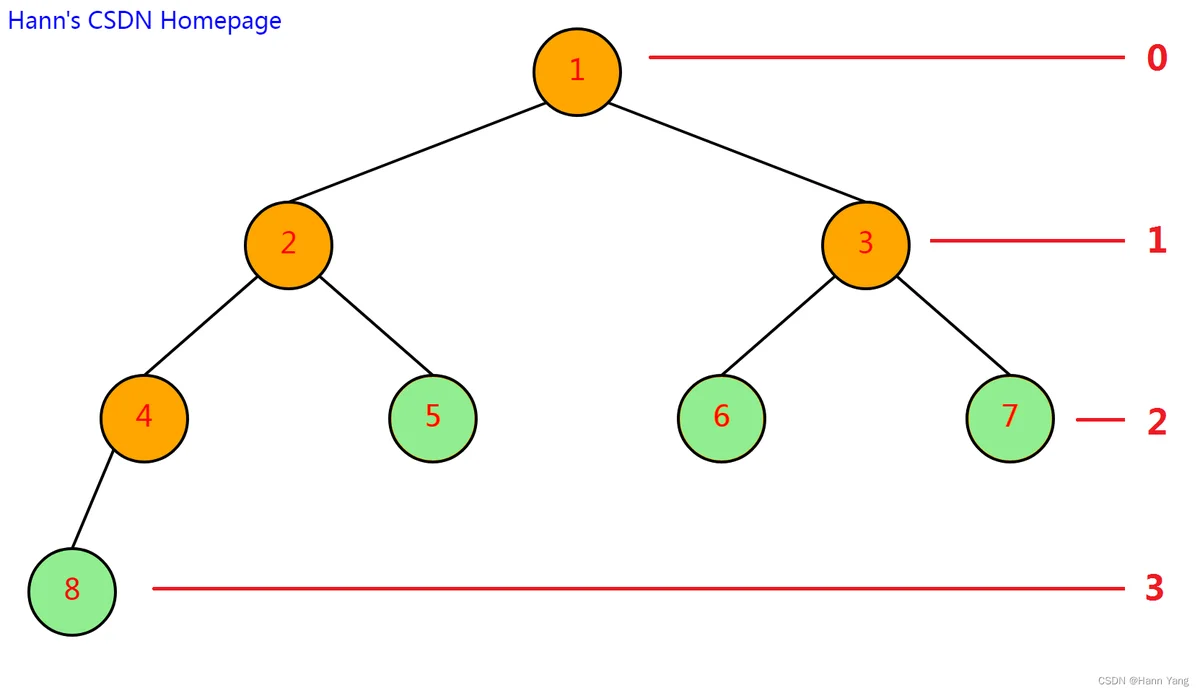
改成返回数组形式如下： 另外也可以把y++,y--改成参数y+1，输出[0 1 2 3 2 1 2 2]，结果相同。
横坐标遍历
依葫芦画瓢，照纵坐标的方式遍历：
但结果不符合要求：1:0 2:-1 4:-2 8:-3 5:0 3:1 6:0 7:2
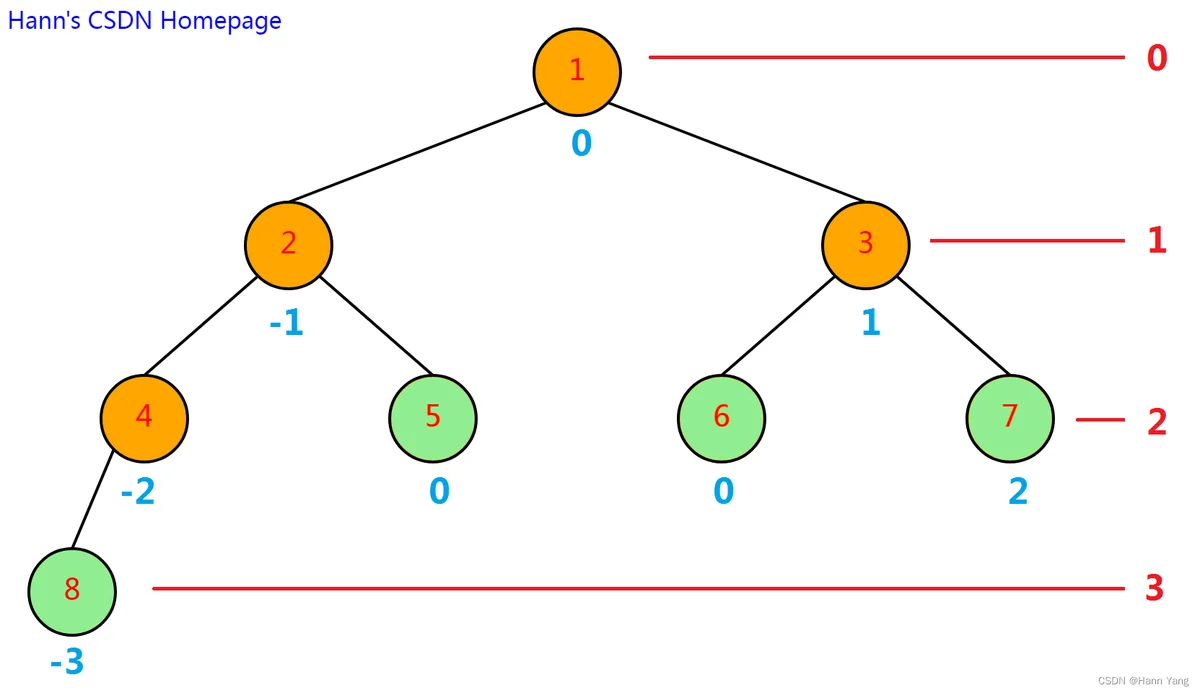
最底下一层最靠近中间的左右两结点横坐标是-1,1就OK了，以满二叉树为例来说比较好理解：
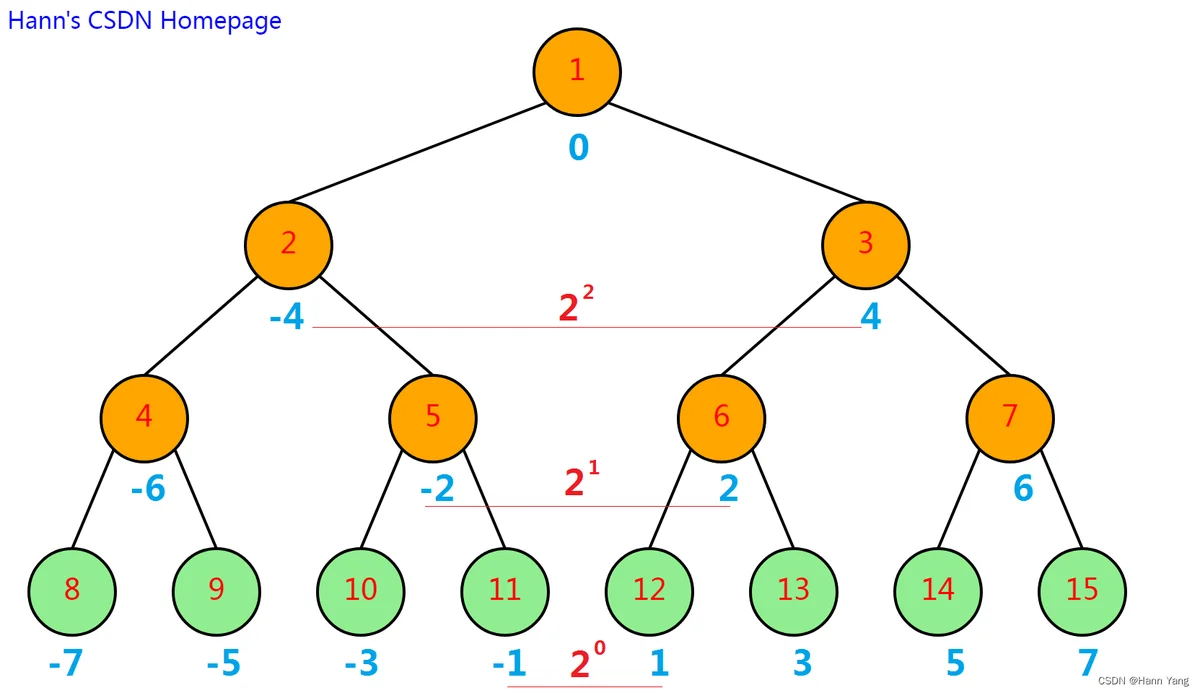
从上图的规律看，每层平移的距离不一样的，不能平移正负1，移动距离应该是2的高度减一次方才对，调用时参数为（0,2的高度-2次方），完整的测试代码如下：
横纵坐标联合输出
综上，把横纵坐标放一起以数组形式输出，参数多一个是变动的平移距离：
至此，坐标遍历全部完成，再加上判断有否左右子树结点就能作图了：
作图时的用法，以上面完整代码的输出为例：
遍历到 2 -4 1 2 true true ，表示(-4,1)处是结点2，true true就有2条子树的连线，指向坐标 (-4-2, 1+1) (-4+2, 1+1)，即 (-6, 2) 和 (-2, 2)，即结点4和结点；
遍历到 4 -6 2 1 true false，表示(-6,2)处是结点4，true false说明它只有左子树，指向坐标 (-7,3)，即结点8；
遍历到 8 -7 3 0 false false，表示(-7,3)处是结点8，false,false说明它是叶结点。
具体如何把结点和坐标转换到二叉树svg图形格式，请参见上篇文章：
《go语言｜数据结构：二叉树可视化（制作svg格式树形图）》。
BTW，以上所有代码不论是哪一个递归遍历都可以有三种顺序，比如坐标遍历的代码：
换个顺序就成为中序和后序遍历：
(本文完)