Golang(五十四)[树 - Golang教程网

1.初始化

mkdir -p binaryTree
cd binaryTree
go mod init binaryTree
touch binaryTree.go
vim binaryTree.go

2.定义二叉树结点结构体

// 定义二叉树结点结构体
type BinaryTreeNode struct {
	// 数据域
	Data interface{}
	// 左子结点
	Lchild *BinaryTreeNode
	// 右子结点
	Rchild *BinaryTreeNode
}

3.根据图创建二叉树

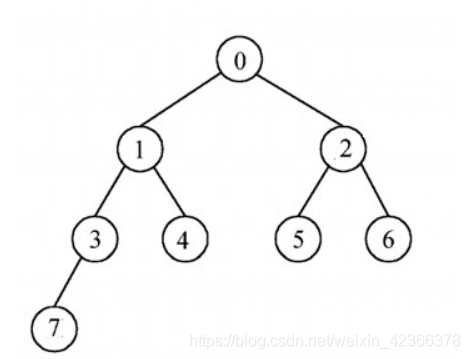
在这里插入图片描述

// 根据图创建二叉树
func (node *BinaryTreeNode) CreateBinaryTree() {
	if node == nil {
		return
	}
	node1 := &BinaryTreeNode{1, nil, nil}
	node2 := &BinaryTreeNode{2, nil, nil}
	node3 := &BinaryTreeNode{3, nil, nil}
	node4 := &BinaryTreeNode{4, nil, nil}
	node5 := &BinaryTreeNode{5, nil, nil}
	node6 := &BinaryTreeNode{6, nil, nil}
	node7 := &BinaryTreeNode{7, nil, nil}

	node.Data = 0
	node.Lchild = node1

	node1.Lchild = node3
	node1.Rchild = node4
	node3.Lchild = node7

	node.Rchild = node2
	node2.Lchild = node5
	node2.Rchild = node6
}

测试

func main() {
	tree := new(BinaryTreeNode)
	tree.CreateBinaryTree()
	fmt.Println(tree) // &{0 0xc0000044c0 0xc0000044e0} // 数据，左子节点，右子节点
}

4.打印二叉树

二叉树的遍历的前提都是【先左右后】

先序、中序、后序遍历是取决于根、如果根在前就是先序DLR（Data，Lchild，Rchild），根在中间即中序LDR（Lchild，Data，Rchild）、根在后就是后序LRD（Lchild，Rchild，Data）

1.先序遍历DLR

根、左子树、右子树

// 打印二叉树---先序遍历DLR：先根、再左、再右
func (node *BinaryTreeNode) PreOrderPrint() {
	// 容错处理，同时也是递归出口
	if node == nil {
		return
	}
	// 根（Data）
	fmt.Print(node.Data, " ")
	// 左子树（Lchild）递归调用
	node.Lchild.PreOrderPrint()
	// 右子树（Rchild）递归调用
	node.Rchild.PreOrderPrint()
}

测试

func main() {
	tree := new(BinaryTreeNode)
	tree.CreateBinaryTree()
	fmt.Println("先序遍历结果：")
	tree.PreOrderPrint()
}

0 1 3 7 4 2 5 6

2.中序遍历LDR

左子树、根、右子树

// 打印二叉树---中序遍历LDR：先左、再根、再右
func (node *BinaryTreeNode) MidOrderPrint() {
	// 容错处理，同时也是递归出口
	if node == nil {
		return
	}
	// 左子树（Lchild）递归调用
	node.Lchild.MidOrderPrint()
	// 根（Data）
	fmt.Print(node.Data, " ")
	// 右子树（Rchild）递归调用
	node.Rchild.MidOrderPrint()
}

测试

func main() {
	tree := new(BinaryTreeNode)
	tree.CreateBinaryTree()
	fmt.Println("中序遍历结果：")
	tree.MidOrderPrint()
}

7 3 1 4 0 5 2 6

3.后序遍历LRD

左子树、右子树、根

// 打印二叉树---后序遍历LRD：先左、再右、再根
func (node *BinaryTreeNode) PostOrderPrint() {
	// 容错处理，同时也是递归出口
	if node == nil {
		return
	}
	// 左子树（Lchild）递归调用
	node.Lchild.PostOrderPrint()

	// 右子树（Rchild）递归调用
	node.Rchild.PostOrderPrint()
	// 根（Data）
	fmt.Print(node.Data, " ")
}

测试

func main() {
	tree := new(BinaryTreeNode)
	tree.CreateBinaryTree()
	fmt.Println("后序遍历结果：")
	tree.PostOrderPrint()
}

7 3 4 1 5 6 2 0

5.获取二叉树高度/深度

// 获取二叉树树高/深度
func (node *BinaryTreeNode) TreeHeight() int {
	// 容错处理，同时也是递归出口
	if node == nil {
		return 0 // 不能返回-1，否则少一个深度
	}
	// 左子树递归探求深度
	lch := node.Lchild.TreeHeight()
	// 右子树递归探求深度
	rch := node.Rchild.TreeHeight()
	if lch > rch {
		// 每一次递归深度自增
		lch++
		return lch
	} else {
		// 每一次递归深度自增
		rch++
		return rch
	}
}

测试

func main() {
	tree := new(BinaryTreeNode)
	tree.CreateBinaryTree()
	th := tree.TreeHeight()
	fmt.Println("二叉树书高：", th)
}

4

6.获取二叉树叶子节点数

// 获取二叉树叶子节点数
func (node *BinaryTreeNode) LeafNumber() (number int) {
	// 容错处理
	if node == nil {
		return
	}
	// 判断是否是叶子节点：左子树为nil，同时右子树也为nil
	if node.Lchild == nil && node.Rchild == nil {
		number++
	}
	// 左子树（Lchild）递归调用
	number += node.Lchild.LeafNumber()
	// 右子树（Rchild）递归调用
	number += node.Rchild.LeafNumber()
	return
}

// 获取二叉树叶子节点数--指针传参
func (node *BinaryTreeNode) LeafNumber2(number *int) {
	// 容错处理
	if node == nil {
		return
	}
	// 判断是否是叶子节点：左子树为nil，同时右子树也为nil
	if node.Lchild == nil && node.Rchild == nil {
		*number++
	}
	// 左子树（Lchild）递归调用
	node.Lchild.LeafNumber2(number)
	// 右子树（Rchild）递归调用
	node.Rchild.LeafNumber2(number)
	return
}

测试

func main() {
	tree := new(BinaryTreeNode)
	tree.CreateBinaryTree()
	number := tree.LeafNumber()
	fmt.Println("二叉树叶子节点：", number)
	num := 0
	tree.LeafNumber2(&num)
	fmt.Println("二叉树叶子节点：", num)
}

4

7.查找二叉树数据

// 查找二叉树数据
func (node *BinaryTreeNode) Search(data interface{}, b *bool) {
	if node == nil || data == nil {
		return
	}
	// 比较数据类型和值是否一致
	if reflect.DeepEqual(node.Data, data) && reflect.TypeOf(node.Data) == reflect.TypeOf(data) {
		*b = true
		return
	}
	// 左子树（Lchild）递归调用
	node.Lchild.Search(data, b)
	// 右子树（Rchild）递归调用
	node.Rchild.Search(data, b)
}

测试

func main() {
	tree := new(BinaryTreeNode)
	tree.CreateBinaryTree()
	number := 13
	b := false
	tree.Search(number, &b)
	fmt.Printf("二叉树是否存在数据 %d : %v\r\n", number, b)
}

8.销毁二叉树

// 销毁二叉树
func (node *BinaryTreeNode) Destroy() {
	if node == nil {
		return
	}
	// 左子树（Lchild）递归调用
	node.Lchild.Destroy()
	// 销毁数据，促使GC工作
	node.Data = nil
	node.Lchild = nil

	// 右子树（Rchild）递归调用
	node.Rchild.Destroy()
	// 销毁数据，促使GC工作
	node.Data = nil
	node.Rchild = nil
}

测试

func main() {
	tree := new(BinaryTreeNode)
	tree.CreateBinaryTree()
	fmt.Println("销毁前：")
	tree.PreOrderPrint()
	fmt.Println()
	tree.Destroy()
	fmt.Println("销毁后:")
	tree.PreOrderPrint()
}

或者可以直接tree = nil

9.翻转（满二叉树）

完全二叉树

除最后一层外，每一层的结点数都达到最大值。（左子、右子都不缺）
“满二叉树” 是“完全二叉树”的特例！

满二叉树

每个结点都有左子结点、右子结点的二叉树。

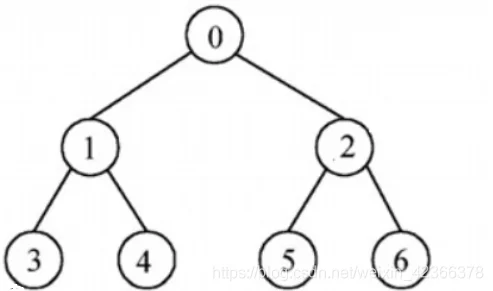
在这里插入图片描述
将创建二叉树的7的叶子节点注释掉形成满二叉树：

// 根据图创建二叉树
func (node *BinaryTreeNode) CreateBinaryTree() {
	if node == nil {
		return
	}
	node1 := &BinaryTreeNode{1, nil, nil}
	node2 := &BinaryTreeNode{2, nil, nil}
	node3 := &BinaryTreeNode{3, nil, nil}
	node4 := &BinaryTreeNode{4, nil, nil}
	node5 := &BinaryTreeNode{5, nil, nil}
	node6 := &BinaryTreeNode{6, nil, nil}
	// node7 := &BinaryTreeNode{7, nil, nil}

	node.Data = 0
	node.Lchild = node1

	node1.Lchild = node3
	node1.Rchild = node4
	// node3.Lchild = node7

	node.Rchild = node2
	node2.Lchild = node5
	node2.Rchild = node6
}

翻转操作

// 二叉树翻转(满二叉树)
func (node *BinaryTreeNode) Reverse() {
	if node == nil {
		return
	}
	// 左子树和右子树交换位置，go的多重赋值实现
	node.Lchild, node.Rchild = node.Rchild, node.Lchild

	// 左子树（Lchild）递归调用
	node.Lchild.Reverse()
	// 右子树（Rchild）递归调用
	node.Rchild.Reverse()
}

测试

func main() {
	tree := new(BinaryTreeNode)
	tree.CreateBinaryTree()
	fmt.Println("翻转前：")
	tree.PreOrderPrint()
	fmt.Println()
	tree.Reverse()
	fmt.Println("翻转后：")
	tree.PreOrderPrint()
}

翻转前：
0 1 3 4 2 5 6
翻转后：
0 2 6 5 1 4 3

10.拷贝

// 拷贝二叉树
func (node *BinaryTreeNode) Copy() *BinaryTreeNode {
	// 容错处理
	if node == nil {
		return nil
	}
	// 左子树（Lchild）递归调用,得到左子树
	oldLChild := node.Lchild.Copy()
	// 右子树（Rchild）递归调用,得到右子树
	oldRChild := node.Rchild.Copy()

	// 创建新结点并赋值
	newBinaryTreeNode := new(BinaryTreeNode)
	newBinaryTreeNode.Data = node.Data
	newBinaryTreeNode.Lchild = oldLChild
	newBinaryTreeNode.Rchild = oldRChild

	return newBinaryTreeNode
}

测试

func main() {
	tree := new(BinaryTreeNode)
	tree.CreateBinaryTree()
	fmt.Println("原二叉树：")
	tree.PreOrderPrint()
	fmt.Println("\r\n拷贝的二叉树：")
	newTree := tree.Copy()
	newTree.PreOrderPrint()
	fmt.Println("\r\n修改拷贝的二叉树，测试修改是否导致原二叉树的变化：")
	newTree.Lchild.Data = 666
	fmt.Println("原二叉树：")
	tree.PreOrderPrint()
	fmt.Println("\r\n拷贝并将左子树的数值修改为666的二叉树：")
	newTree.PreOrderPrint()
}

原二叉树：
0 1 3 7 4 2 5 6
拷贝的二叉树：
0 1 3 7 4 2 5 6
修改拷贝的二叉树，测试修改是否导致原二叉树的变化：
原二叉树：
0 1 3 7 4 2 5 6
拷贝并将左子树的数值修改为666的二叉树：
0 666 3 7 4 2 5 6

11.完整代码

package main

import (
	"fmt"
	"reflect"
)

// 定义二叉树结点结构体
type BinaryTreeNode struct {
	// 数据域
	Data interface{}
	// 左子结点
	Lchild *BinaryTreeNode
	// 右子结点
	Rchild *BinaryTreeNode
}

// 根据图创建二叉树
func (node *BinaryTreeNode) CreateBinaryTree() {
	if node == nil {
		return
	}
	node1 := &BinaryTreeNode{1, nil, nil}
	node2 := &BinaryTreeNode{2, nil, nil}
	node3 := &BinaryTreeNode{3, nil, nil}
	node4 := &BinaryTreeNode{4, nil, nil}
	node5 := &BinaryTreeNode{5, nil, nil}
	node6 := &BinaryTreeNode{6, nil, nil}
	node7 := &BinaryTreeNode{7, nil, nil}

	node.Data = 0
	node.Lchild = node1

	node1.Lchild = node3
	node1.Rchild = node4
	node3.Lchild = node7

	node.Rchild = node2
	node2.Lchild = node5
	node2.Rchild = node6
}

// 打印二叉树---先序遍历DLR：先根、再左、再右
func (node *BinaryTreeNode) PreOrderPrint() {
	// 容错处理，同时也是递归出口
	if node == nil {
		return
	}
	// 根（Data）
	fmt.Print(node.Data, " ")
	// 左子树（Lchild）递归调用
	node.Lchild.PreOrderPrint()
	// 右子树（Rchild）递归调用
	node.Rchild.PreOrderPrint()
}

// 打印二叉树---中序遍历LDR：先左、再根、再右
func (node *BinaryTreeNode) MidOrderPrint() {
	// 容错处理，同时也是递归出口
	if node == nil {
		return
	}
	// 左子树（Lchild）递归调用
	node.Lchild.MidOrderPrint()
	// 根（Data）
	fmt.Print(node.Data, " ")
	// 右子树（Rchild）递归调用
	node.Rchild.MidOrderPrint()
}

// 打印二叉树---后序遍历LRD：先左、再右、再根
func (node *BinaryTreeNode) PostOrderPrint() {
	// 容错处理，同时也是递归出口
	if node == nil {
		return
	}
	// 左子树（Lchild）递归调用
	node.Lchild.PostOrderPrint()

	// 右子树（Rchild）递归调用
	node.Rchild.PostOrderPrint()
	// 根（Data）
	fmt.Print(node.Data, " ")
}

// 获取二叉树树高/深度
func (node *BinaryTreeNode) TreeHeight() int {
	// 容错处理，同时也是递归出口
	if node == nil {
		return 0 // 不能返回-1，否则少一个深度
	}
	// 左子树递归探求深度
	lch := node.Lchild.TreeHeight()
	// 右子树递归探求深度
	rch := node.Rchild.TreeHeight()
	if lch > rch {
		// 每一次递归深度自增
		lch++
		return lch
	} else {
		// 每一次递归深度自增
		rch++
		return rch
	}
}

// 获取二叉树叶子节点数
func (node *BinaryTreeNode) LeafNumber() (number int) {
	// 容错处理
	if node == nil {
		return
	}
	// 判断是否是叶子节点：左子树为nil，同时右子树也为nil
	if node.Lchild == nil && node.Rchild == nil {
		number++
	}
	// 左子树（Lchild）递归调用
	number += node.Lchild.LeafNumber()
	// 右子树（Rchild）递归调用
	number += node.Rchild.LeafNumber()
	return
}

// 获取二叉树叶子节点数--指针传参
func (node *BinaryTreeNode) LeafNumber2(number *int) {
	// 容错处理
	if node == nil {
		return
	}
	// 判断是否是叶子节点：左子树为nil，同时右子树也为nil
	if node.Lchild == nil && node.Rchild == nil {
		*number++
	}
	// 左子树（Lchild）递归调用
	node.Lchild.LeafNumber2(number)
	// 右子树（Rchild）递归调用
	node.Rchild.LeafNumber2(number)
	return
}

// 查找二叉树数据
func (node *BinaryTreeNode) Search(data interface{}, b *bool) {
	if node == nil || data == nil {
		return
	}
	// 比较数据类型和值是否一致
	if reflect.DeepEqual(node.Data, data) && reflect.TypeOf(node.Data) == reflect.TypeOf(data) {
		*b = true
		return
	}
	// 左子树（Lchild）递归调用
	node.Lchild.Search(data, b)
	// 右子树（Rchild）递归调用
	node.Rchild.Search(data, b)
}

// 销毁二叉树
func (node *BinaryTreeNode) Destroy() {
	if node == nil {
		return
	}
	// 左子树（Lchild）递归调用
	node.Lchild.Destroy()
	// 销毁数据，促使GC工作
	node.Data = nil
	node.Lchild = nil

	// 右子树（Rchild）递归调用
	node.Rchild.Destroy()
	// 销毁数据，促使GC工作
	node.Data = nil
	node.Rchild = nil
}

// 二叉树翻转(满二叉树)
func (node *BinaryTreeNode) Reverse() {
	if node == nil {
		return
	}
	// 左子树和右子树交换位置，go的多重赋值实现
	node.Lchild, node.Rchild = node.Rchild, node.Lchild

	// 左子树（Lchild）递归调用
	node.Lchild.Reverse()
	// 右子树（Rchild）递归调用
	node.Rchild.Reverse()
}

// 拷贝二叉树
func (node *BinaryTreeNode) Copy() *BinaryTreeNode {
	// 容错处理
	if node == nil {
		return nil
	}
	// 左子树（Lchild）递归调用,得到左子树
	oldLChild := node.Lchild.Copy()
	// 右子树（Rchild）递归调用,得到右子树
	oldRChild := node.Rchild.Copy()

	// 创建新结点并赋值
	newBinaryTreeNode := new(BinaryTreeNode)
	newBinaryTreeNode.Data = node.Data
	newBinaryTreeNode.Lchild = oldLChild
	newBinaryTreeNode.Rchild = oldRChild

	return newBinaryTreeNode
}
func main() {
	tree := new(BinaryTreeNode)
	tree.CreateBinaryTree()
	fmt.Println("原二叉树：")
	tree.PreOrderPrint()
	fmt.Println("\r\n拷贝的二叉树：")
	newTree := tree.Copy()
	newTree.PreOrderPrint()
	fmt.Println("\r\n修改拷贝的二叉树，测试修改是否导致原二叉树的变化：")
	newTree.Lchild.Data = 666
	fmt.Println("原二叉树：")
	tree.PreOrderPrint()
	fmt.Println("\r\n拷贝并将左子树的数值修改为666的二叉树：")
	newTree.PreOrderPrint()
}