有些程序员也把栈称为堆栈, 即栈和堆栈是同一个概念
1) 栈的英文为(stack)
2) 栈是一个先入后出(FILO-First In Last Out)的有序列表。
3) 栈(stack)是限制线性表中元素的插入和删除只能在线性表的同一端进行的一种特殊线性表。允许插入和删除的一端,为变化的一端,称为栈顶(Top),另一端为固定的一端,称为栈底(Bottom)。
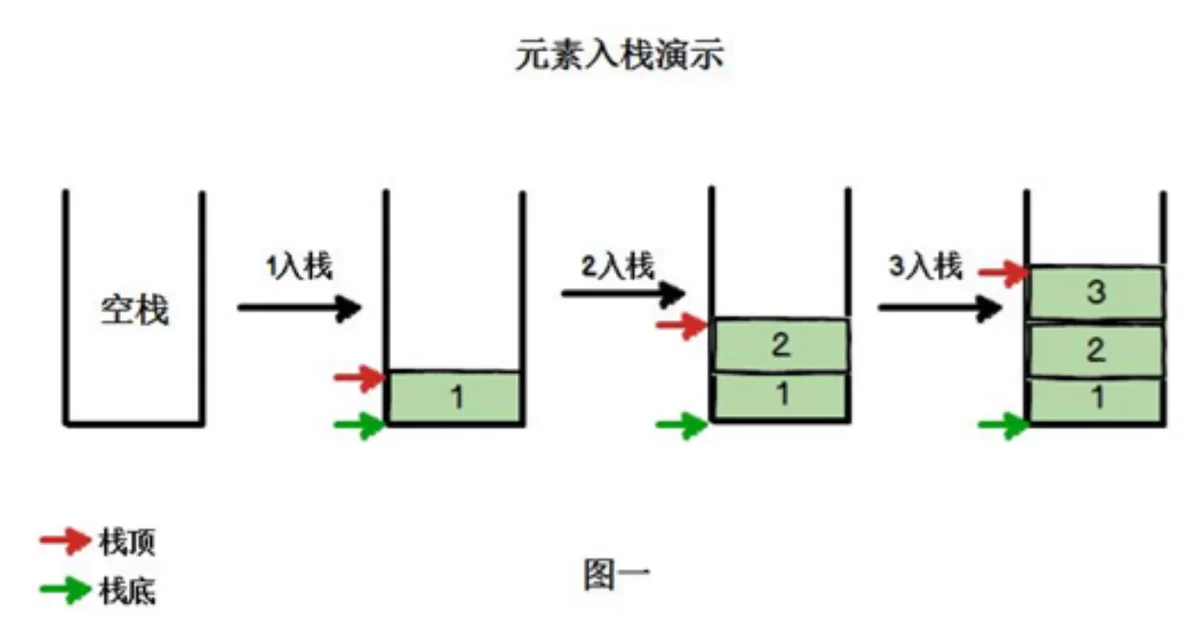
4) 根据堆栈的定义可知,最先放入栈中元素在栈底,最后放入的元素在栈顶,而删除元素刚好相反,最后放入的元素最先删除,最先放入的元素最后删除
1.1. 示意图
入栈
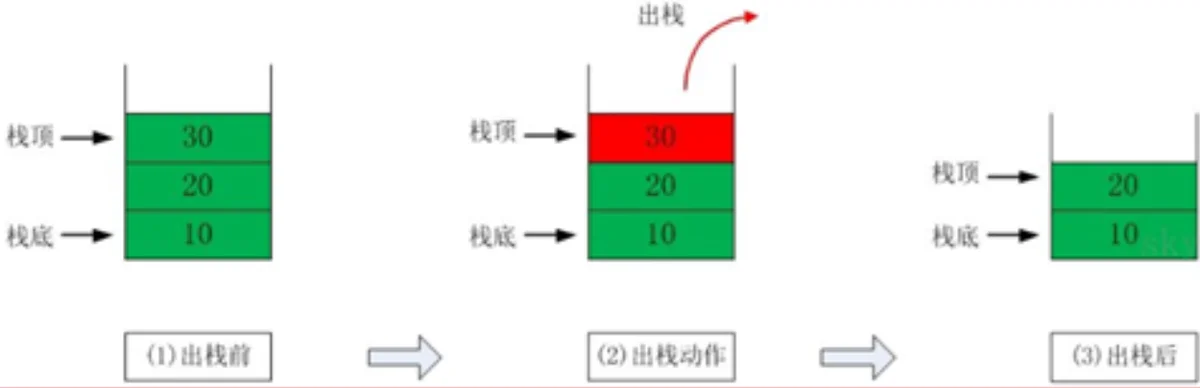
出栈
1.2. 场景
1) 子程序的调用:在跳往子程序前,会先将下个指令的地址存到堆栈中,直到子程序执行完后再 将地址取出,以回到原来的程序中。
2) 处理递归调用:和子程序的调用类似,只是除了储存下一个指令的地址外,也将参数、区域变 量等数据存入堆栈中。
3) 表达式的转换与求值。
4) 二叉树的遍历。
5) 图形的深度优先(depth 一 first)搜索法。
1.3. 案例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
package main
import (
"errors"
"fmt"
)
type Stack struct {
maxNum int //规定栈最多放几个元素
top int //目前栈顶的下标
arr [5]int //模拟栈
}
func (this *Stack) Push(val int) (err error) {
if this.isFull() {
fmt.Println("stack full")
err = errors.New("stack full")
return
}
//开始入栈操作
//先向上走一步
this.top++
//再赋值
this.arr[this.top] = val
return
}
func (this *Stack) Pop() (val int, err error) {
if this.isEmpty() {
fmt.Println("stack empty")
err = errors.New("stack empty")
return
}
val = this.arr[this.top]
this.top--
return
}
func (this *Stack) List() (err error) {
if this.isEmpty() {
fmt.Println("stack empty")
err = errors.New("stack empty")
return
}
for i := this.top; i >= 0; i-- {
fmt.Printf("arr[%d]=%d\n", i, this.arr[i])
}
return
}
func (this *Stack) isFull() bool {
return this.top+1 >= this.maxNum
}
func (this *Stack) isEmpty() bool {
return this.top == -1
}
func main() {
var stack = &Stack{
maxNum: 5,
top: -1,
}
stack.Push(1)
stack.Push(2)
stack.Push(3)
stack.Push(4)
stack.Push(5)
stack.List()
val, _ := stack.Pop()
fmt.Println("弹出 ", val)
stack.List()
}
1.4. 栈的计算表达式
1.4.1. 分析

1.4.2. 实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
package main
import (
"errors"
"fmt"
"strconv"
)
type Stack struct {
maxNum int //规定栈最多放几个元素
top int //目前栈顶的下标
arr [20]int //模拟栈
}
func (this *Stack) Push(val int) (err error) {
if this.isFull() {
fmt.Println("stack full")
err = errors.New("stack full")
return
}
//开始入栈操作
//先向上走一步
this.top++
//再赋值
this.arr[this.top] = val
return
}
func (this *Stack) Pop() (val int, err error) {
if this.isEmpty() {
fmt.Println("stack empty")
err = errors.New("stack empty")
return
}
val = this.arr[this.top]
this.top--
return
}
func (this *Stack) List() (err error) {
if this.isEmpty() {
fmt.Println("stack empty")
err = errors.New("stack empty")
return
}
for i := this.top; i >= 0; i-- {
fmt.Printf("arr[%d]=%d\n", i, this.arr[i])
}
return
}
func (this *Stack) isFull() bool {
return this.top+1 >= this.maxNum
}
func (this *Stack) isEmpty() bool {
return this.top == -1
}
//判断是不是运算符
func (this *Stack) isOper(oper int) bool {
if oper == 42 || oper == 43 || oper == 45 || oper == 47 {
return true
}
return false
}
//计算
func (this *Stack) cal(num1, num2, oper int) int {
//因为栈是先进后出,所以num2应该是第一个数,num1是第二个数
switch oper {
case 42:
return num2 * num1
case 43:
return num2 + num1
case 45:
return num2 - num1
case 47:
return num2 / num1
default:
fmt.Println("运算符错误")
}
return 0
}
//返回优先级
func (this *Stack) Priority(oper int) int {
if oper == 42 || oper == 47 {
return 1
} else if oper == 43 || oper == 45 {
return 0
}
return -1
}
func main() {
numStack := &Stack{ //数栈
maxNum: 20,
top: -1,
}
operStack := &Stack{ //运算符栈
maxNum: 20,
top: -1,
}
exp := "300+600*2-18*5"
exp_len := len(exp)
num1 := 0
num2 := 0
oper := 0
var num_str string
//将表达式入栈并且进行计算
for i := 0; i < exp_len; i++ {
ch := int(exp[i]) //返回的是asiic码值
if operStack.isOper(ch) {
//如果放进去的是运算符
//需要先考虑是不是第一个元素
if operStack.isEmpty() {
//如果是空,代表第一个元素,直接入栈
operStack.Push(ch)
} else {
//如果不是第一个元素,则需要考虑,此时栈顶元素的优先级是否大于等于当前想要入栈的值
if operStack.Priority(operStack.arr[operStack.top]) >= operStack.Priority(ch) {
//无需担心数量是否不匹配,只要表达式正确,数量一定没问题
//从数栈中弹出2个
num1, _ = numStack.Pop()
num2, _ = numStack.Pop()
//运算符栈弹出一个
oper, _ = operStack.Pop()
//运算结果入数栈(这里num1,num2顺序不能错乱,因为是先进后出)
numStack.Push(numStack.cal(num1, num2, oper))
//运算符入运算符栈
operStack.Push(ch)
} else {
//不成立的话,证明运算符级别相同,直接入栈
operStack.Push(ch)
}
}
} else {
//如果放进去的是数字
//此时需要考虑,数字有几位数
//数字是否是最后一位
temp := i
num_str = string(ch) //将asiic用string强转,返回的是对应的字符
for {
if temp+1 != exp_len && !operStack.isOper(int(exp[temp+1])) {
//如果下一位既不是字符串最后一个或者不是运算符
//那么就加入到num_str,累计字符串
num_str += string(exp[temp+1])
} else {
//否则就是不符合,直接退出
break
}
temp++
}
//将拼接后的字符串转为数字
num, _ := strconv.Atoi(num_str)
//是数字就不需要考虑,直接入栈
numStack.Push(num)
//同时,让for循环走到temp的位置
i = temp
//清空内容
num_str = ""
}
}
//将栈内剩余的表达式再进行运算
for {
if operStack.isEmpty() {
//如果运算符为空,证明全部计算完成,直接退出
break
}
//否则进行计算
num1, _ = numStack.Pop()
num2, _ = numStack.Pop()
//运算符栈弹出一个
oper, _ = operStack.Pop()
//运算结果入数栈(这里num1,num2顺序不能错乱,因为是先进后出)
numStack.Push(numStack.cal(num1, num2, oper))
}
//全部计算完成,弹出numStack就是结果
result, _ := numStack.Pop()
fmt.Printf("%s = %v \n", exp, result)
}
