CTC的想法很难懂,尤其是对前向后向算法不熟的人,然后再网上发现了一篇很好的教程,我把它翻译了下来,里面有大量的例子,专注于原理的讲解,非常透彻,不像CTC的原论文,那样全面冗长,希望也能帮助大家理解。我在五六月份找过其它中文资料,发现原理详解的很少,我特地弥补一下中文这一块的空缺。
介绍
Connectionist Temporal Classification (CTC)是一项技术,它是为RNN专门设计的顶层(top layer)。使得针对输入序列的每一帧,网络能够输出一个标签或者空白(blank)。CTC使得用一个RNN构建语音识别系统成为可能,这个和混合方法HMM+DNN不一样。
语音识别问题
输入是一个声音片段x,然后分割成很多个帧:
X={x1,…,xT}
每一帧在时刻t,用xt表示,xt由G个声谱的权重组成:
Xt=[xt1,…,xt,G]T
我们可以设计一个RNN对每一帧xt的输出yt::
Y={y1,…,yT}
Yt是一个字母表的概率分布:
Yt=[yt,1…yt,K]T
其中yt,k和lt代表在时刻t发音字母。
那么,问题来了,我们怎样把y解释成一串字母。
首先,很直接,我们要找一个路径
Π={π1…πT}
其中πt属于[1,K]
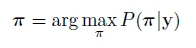
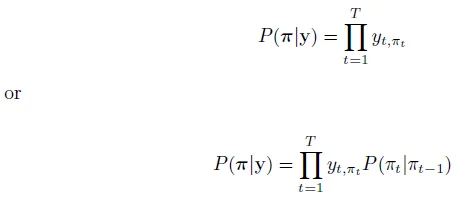
设想一个人说了一个“a”,在说之前,之后有一个安静的部分(silence),路径π可以是:
aaaaaaaa
aaaaa___
____aaaa
__aaaaa_
但这个没考虑到安静期和发音的变化,下面这个例子所有对应 “a”的路径:
aa______
aaa_____
_aaa____
___aaaa_
_aaaaaaa
上面的例子告诉我们,网络的输出既不是y也不是π。而是一些叫做标签的序列,用l表示:
L={l1,…,lS}
其中S<=T
对于上面的例子,所有那些路径都是对应样本标签:l={a}.
所有下面的样例对应l={h,e}:
hhheeee
__heeee
_hee___
hh__eee
_hh_eee
h__ee__
__h_ee_
注意空白(blanks)可以出现在he之前,之间,之后。
更复杂一点的例子是l={b,e,e}:
bbbeee_ee
_bb_ee__e
__bbbe_e_
但下面的例子对应l={b,e}
_b_eeeeee
bbb__eeee
_bb_eee__
这两个例子显示了空白在分开连续重复字母的重要性。
综上,语音识别的输出并不是字母表的分布y或者路径π,而是标签l.CTC 是从y结合π来推出l的方法。
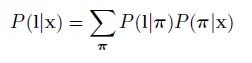
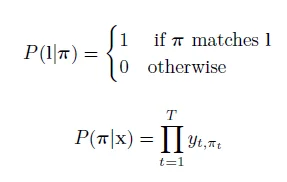
Y的长度可能和l的长度不一样,因此从y推理(inference)l实际上是动态时间规整问题。动态时间规整算法使得我们可以用(x,l)对进行训练,而不是(x,y)对,这是非常有价值的,因为我们在训练前不需要预先分割y,并且把x和y对齐。
时间规整的意思是我们想要把yt映射到某个ls.由上述的例子我们其实是想要把yt 映射到要么是ls,要么是一个空白。因为要是我们这样做了,我们就有机会识别后继字母,比如coffee中“ff”,bee中的”ee“。
假设我们有一个“bee”的语音片段,最可能的路径π是:
___bbeeee____
我们想要把它规整到l={b,e,e},好像我们可以建立下面的映射:
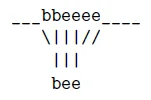
但是事实是我们没有太多信息去组织算法把所有的e映射到l中的第一个e:
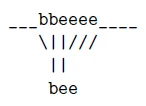
另一个问题是我们应该把这些空白(blanks)映射到π中的哪一个。
一个解决办法就是我们把π映射到l’,我们在l之前,中间,后面都插入blank就构成了l’,对于上面的例子,我们就可以得到:
L’={,b,,e,,e,}
就有了下面的规整:
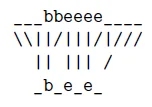
但有时π中的第一个字符不是空白,所以我们可以把第一帧对应到‘b’,而不是对应l’中的空白:
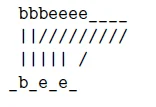
一个相似的情况是π中没有对齐的空白,因此没有帧可以对齐l’中的空白。所以这两种情况都需要我们设计一个算法计算π和l’的映射。
前向后向算法
这里我们推导用于计算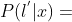 ,很显然他和
,很显然他和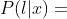 等价,因为
等价,因为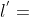 在给定l的情况下构造是唯一的
在给定l的情况下构造是唯一的
1.前向算法
上面的规整的例子说明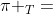 可以映射到要么
可以映射到要么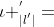 ,即
,即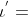 的空白,要么
的空白,要么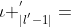 ,根据
,根据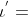 的构造法则,即l的最后一个元素。
的构造法则,即l的最后一个元素。
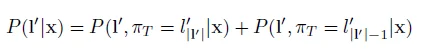
可以写成下面的形式:
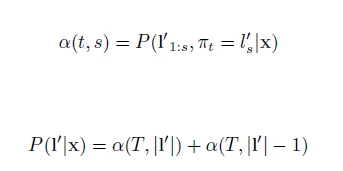
在上面例子中,π1可以映射到要么是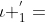 ,即的第一个空白;要么是
,即的第一个空白;要么是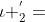 ,l 的第一个元素。因此:
,l 的第一个元素。因此:
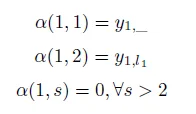
假设我们有l’={_,h,_,e,_}和一串序列y,因此有以下两种情况:


紧接着我们用一个更通用的方法去映射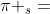 .大体上,我们可以这样映射一个
.大体上,我们可以这样映射一个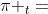 到:
到:
1. 
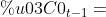 ,用
,用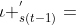 表示
表示
2. 紧挨着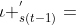 的元素,用
的元素,用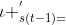 表示,或者
表示,或者
3. 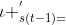 ,如果
,如果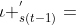 ="_"
="_"
第三个情况是我们想跳过空白,即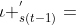 ="_".
="_".
一个例子:我们想要把π={h,h,h,h,e,e,e}映射到l’={_,h,_,e,_}
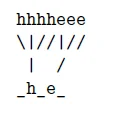
但是,当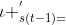 的时候,上述第3种情况是不合理的。在这种情况下,我们不应该跳过空白。例如,当识别单词bee的时候,l’={_,b ,_,e ,_,e ,_},在这种情况下,当我们跳过两个e之间的空格,我们就会把两个e错误地当成了一个e.在下面这个样例中,即使我们把这帧(y5)听起来更像一个e而不是空白,我们还是想要把它映射成空白,即
的时候,上述第3种情况是不合理的。在这种情况下,我们不应该跳过空白。例如,当识别单词bee的时候,l’={_,b ,_,e ,_,e ,_},在这种情况下,当我们跳过两个e之间的空格,我们就会把两个e错误地当成了一个e.在下面这个样例中,即使我们把这帧(y5)听起来更像一个e而不是空白,我们还是想要把它映射成空白,即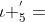 ="_",因此我们识别出了bee这个单词。
="_",因此我们识别出了bee这个单词。
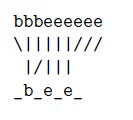
综上,我们可得:
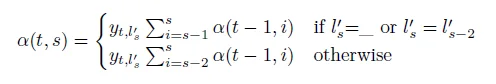
2.后向算法
和前向变量α(t ,s)相似,我们定义后向变量β(t ,s)
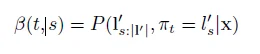
由于时间规整把πT映射到要么是 ,,即用1的概率对齐空白,要么
,,即用1的概率对齐空白,要么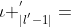 ,即l集合中最后一个元素,概率为1,即:
,即l集合中最后一个元素,概率为1,即:
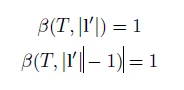
和前向算法的泛华规则相似,我们有:
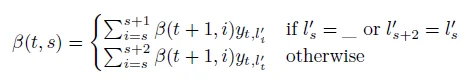
搜索空间
计算α(t ,s)的时候,我们需要α(t-1 ,s),α(t-1 ,s-1),α(t-1 ,s-2)。为了计算β(t,s),我们需要β(t+1,s),β(t+1,s+1),β(t+1,s+2)。其中的一些值为0,如图:
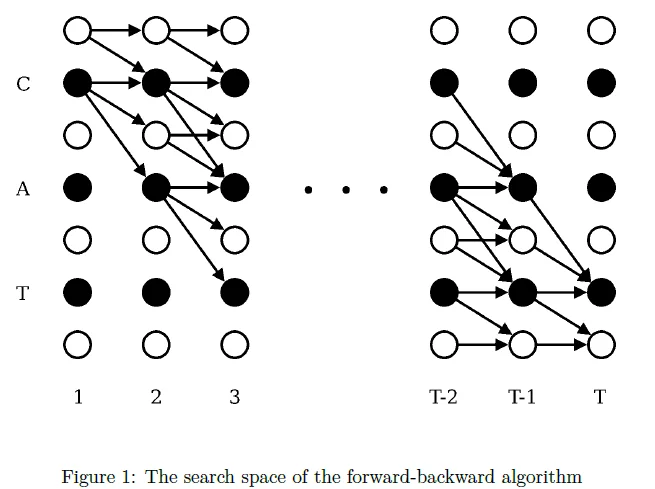
每个圈代表搜索空间的一个可能状态,这些状态以t和s的各自对齐,箭头连接一个状态和另一个状态,当我们计算α(t ,s)的时候,我们不需要进入不可能的区域,即右上角的的连接状态。
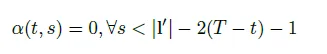
当我们计算β(t ,s)的时候,我们不可能进入左下角的状态:
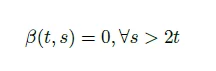
为了约束动态规划算法(dynamic programming algorithm),我们需要下列条件:
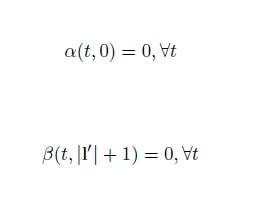
参考文献
[1]. Connectionist Temporal Classification:A Tutorial with Gritty Details.
https://cxwangyi.wordpress.com/2015/10/07/connectionist-temporal-classification-the-gritty-details/
