今天想试试自己的golang功底,所以想用go实现各种快排,假设我们的测试例子是这样的:
// 测试代码
import (
"fmt"
"math/rand"
)
func main() {
// 测试数据随机产生100以内的10个数
data := []int{}
for i := 0; i < 10; i++ {
data = append(data, rand.Intn(100))
}
// 调用各种快排函数
xxx_sorting(data)
// 打印结果
for i := 0; i < len(data); i++ {
fmt.Printf("%d,", data[i])
}
fmt.Printf("\n")
}随机函数产生的数字可能存在重复,但是对于快排来说无所谓。我们先从最原始的冒泡法开始:
// 冒泡法
func bubble_sorting(data []int) {
// 为什么遍历长度是len(data)-1,因为冒泡法采用的是左右两个元素比较的方法
// 就剩下一个元素没有其他元素比较了,也就是有序的
for i := 0; i < len(data)-1; i++ {
// 从小到大排序
for j := 0; j < len(data)-i-1; j++ {
// 如果左边比右边大就交换
if data[j] > data[j+1] {
// 这种写法对于C/C++程序猿来说不可想象
data[j], data[j+1] = data[j+1], data[j]
}
}
}
}其实冒泡法还有很多改良的方法,我更推崇的是这种方法:无序的数可能部分是有序的,尤其是冒泡了几次后,剩余部分很有可能部分有序。所以我的改良方法是:
// 改良的冒泡法,用一个变量记录从第0个元素开始连续多少个元素是有序的
func bubble_sorting(data []int) {
// 用一个变量记录从0开始的元素已经连续几个是有序的,这里的有序指的不是全局的序
// 是在ordered_size范围内是有序的,这样这个范围里的元素就不用在重复比较了,默认肯定是0
ordered_size := 0
// 这里和普通冒泡法是一样的
for i := 0; i < len(data)-1; i++ {
// 因为前面连续ordered_size个元素已经有序了,我们只要从有序的最后一个元素开始就行了
// 这个循环结束的位置len(data)-i-1,-1的原因是比较的是data[j]和data[j+1]
for j := ordered_size; j < len(data)-i-1; j++ {
// 这块和普通的冒泡没什么区别
if data[j] > data[j+1] {
data[j], data[j+1] = data[j+1], data[j]
// 此处判断的目的是当前的元素还在有序范围内,由于这个元素已经和后面的元素交换了
// 后面的元素很可能比ordered_size - 1那个元素还要小,所以连续有序的数量就要-1
// 因为连续有序的数量最小就是0,所以做一个判断,避免出现负数
// ordered_size == j目的是判断当前索引是否还在连续有序的范围
if ordered_size == j && ordered_size > 0 {
ordered_size--
}
// 当前位置已经超出了连续有序范围就不用关心,如果没有,那么当前元素和前面的元素是有序的
} else if ordered_size == j {
ordered_size++
}
}
}
}上面的冒泡改良法在排序过程中前面元素有序加速效果比较明显,如果中间某些元素有序那就没什么效果了。有人肯定会说,那就把刚交换的元素放到有序的位置上不就可以了么,这就是我们接下来介绍的直接插入法。直接插入法的思想如下图:

初始状态有序的元素数量肯定只有1个 ,通过遍历剩余的元素,然后按序插入到制定位置就可以了。代码实现如下:
// 直接插入法
func insert_sorting(data []int) {
// 第一个元素已经有序了,从第二个元素开始遍历
for i := 1; i < len(data); i++ {
// 倒着比较,直到找到合适位置
for j := i; j > 0; j-- {
// 如果比左面的元素大,那就算找到位置了
if data[j-1] < data[j] {
break
}
// 如果比左边的元素小,那么就要交换了
data[j-1], data[j] = data[j], data[j-1]
}
}
}如果说直接插入法还要面临大量的交换的话,选择排序可能是更好的选择,别小看交换数据,涉及到两次的数据读取和存储,如果都是内存数据,数据的访问开销也要考虑进来。选择排序的思想如下图所示:

在无序的元素内选择最小的放在有序元素的后面,此时有序元素数量的初始值为0,代码实现如下:
// 选择排序
func select_sorting(data []int) {
// 因为有序元素数量是0,初始状态所有元素都是无序的
for i := 0; i < len(data)-1; i++ {
// 假设第i个元素就是最小的
k := i
// 寻找最小的元素
for j := i + 1; j < len(data); j++ {
// 每次只记录索引,所以没有交换数据
if data[j] < data[k] {
k = j
}
}
// 只有到最后才交换一次数据,而且还做了判断,如果第i个元素就是最小的,也就不用交换了
if k != i {
data[k], data[i] = data[i], data[k]
}
}
}前面介绍的这些排序方法复杂度都在n(n-1)/2,接下来我们实现一种时间复杂度在nlog(n)的算法,叫做归并法。归并法是将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。归并法的思想如下图所示(图片非原创,引用自互联网):
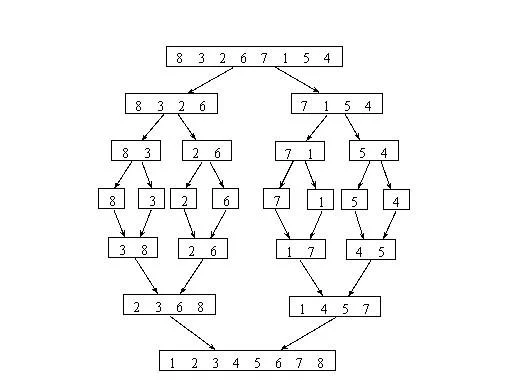
代码实现为:
// 归并排序法,因为用了递归,所以需要传入起始位置,结束为止,以及缓冲,这个缓冲是和data一样大小
func merge_sorting(data []int, start int, end int, buf []int) {
// 如果元素数量超过2个,那就在继续二分
if start+1 < end {
// 二分
mid := (start + end) / 2
// 递归
merge_sorting(data, start, mid, buf)
merge_sorting(data, mid+1, end, buf)
// 合并两个有序的数组
merge(data, start, end, mid, buf)
// 2个或者1个,只有一种条件就是左面的比右边的大才需要交换,其他条件都不需要操作
} else if data[start] > data[end] {
data[start], data[end] = data[end], data[start]
}
}
// 合并有序数组
func merge(data []int, start int, end int, mid int, buf []int) {
// index是合并后数组的索引,left是左半部分有序数组的索引,right是右半部分有序数组的索引
index, left, right := start, start, mid+1
for {
// 假设左边的是最小的
min := left
if data[left] <= data[right] {
left++
// 如果是右半部分的最小
} else {
min = right
right++
}
// 二者最小的元素放到缓冲中
buf[index] = data[min]
index++
// 一旦有哪个半部分数组提前没有元素了就提前结束了
if left > mid || right >= end {
break
}
}
// 把剩下的左半部分合并到缓冲中
for i := left; i <= mid; i++ {
buf[index] = data[i]
index++
}
// 把剩下的右半部分合并到缓冲中
for i := right; i <= end; i++ {
buf[index] = data[i]
index++
}
// 把排好序的缓冲中的数据拷贝到数据内存中
for i := start; i <= end; i++ {
data[i] = buf[i]
}
}归并法的确定是需要O(n)的临时空间,同时还要搬移2O(n)次数据,而大多数标准库都支持的快速排序的临时空间只有O(1),搬移次数也只有O(n),时间复杂度也同样是nlog(n)。快速排序的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
如何做到一部分数据都比另一部分数据小?只要在序列中选择一个数据,比这个数据小的放在左边,比这个数据大的放在右边。在选择数方面有很多方法,可以选择第一个,可以选择中间对的那个,也可以随机选择,我们的实现选择第一个数作为基准。实现代码如下:
// 快速排序实现,由于要二分递归,所以要传入每次排序的起始和结束的索引
func quick_sorting(data []int, start, end int) {
if (start < end) {
// 获取基准值
base := data[start]
// 临时变量,左右索引
left := start
right := end
// 进入循环
for left < right {
// 由于左边的(第0个)被取走当成基准值,所以在左边就留下一个洞,用于存储比基准小的值
// 所以先从右边找,找到第一个比基准值小的
for left < right && data[right] >= base {
right--
}
// 找到了比基准值小的,那就把这个值填入左边的洞,做索引要++
if left < right {
data[left] = data[right]
left++
}
// 因为上面的操作让右边留了一个洞,开始从左边找比基准值大的
for left < right && data[left] <= base {
left++
}
// 找到比基准值大的再次把右边洞填上,并且在左边又留了一个洞
if left < right {
data[right] = data[left]
right--
}
}
// 把基准值填入到洞中,这就是本应该他所在的位置
data[left] = base
// 继续分两组递归排序,注意此时基准值已经不用参与排序了
quick_sorting(data, start, left - 1)
quick_sorting(data, left + 1, end)
}
}
