（28）Go邻接矩阵和邻接表实现有权图

继上一篇《（27）Go实现邻接矩阵和邻接表无权图》后续：
https://www.jianshu.com/p/ad9fed1836d9

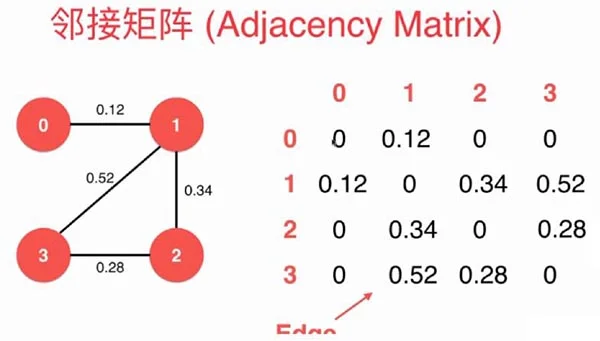
邻接矩阵实现有权图
// 边类
type Edge struct {
	a      int     //a节点
	b      int     //b节点
	weight float64 //权值
}

func newEdge(a, b int, weight float64) *Edge {
	return &Edge{
		a:      a,
		b:      b,
		weight: weight,
	}
}

// 比较两个边的权值
func lessWeight(a, b *Edge) bool {
	return a.weight <= b.weight
}

// 有权稠密图 - 邻接矩阵
type weightedDenseGraph struct {
	n        int  //节点数
	m        int  //边数
	directed bool //有向图 or 无向图
	graph    [][]*Edge
}

// 构造函数:有n个顶点,有向 or 无向图
func NewWeightDenseGraph(n int, directed bool) *weightedDenseGraph {
	// 初始化 n*n 的二维切片矩阵
	buf := make([][]*Edge, n)
	for i := 0; i < n; i++ {
		buf[i] = make([]*Edge, n)
	}
	return &weightedDenseGraph{
		n:        n,
		m:        0,
		directed: directed,
		graph:    buf,
	}
}

// 获取顶点数量
func (d weightedDenseGraph) GetVertex() int {
	return d.n
}

// 获取边数量
func (d weightedDenseGraph) GetEdge() int {
	return d.m
}

// 添加边: v1,v2均表示顶点相应的索引
func (d *weightedDenseGraph) AddEdge(v1, v2 int, weight float64) error {
	b, err := d.HasEdge(v1, v2)
	if err != nil {
		return err
	}

	// 包含两种情况:有边则覆盖原先的边,无边则新添加边
	d.graph[v1][v2] = newEdge(v1, v2, weight)
	if !d.directed {
		// 如果是无向图,v2 -> v1也要表示有边
		d.graph[v2][v1] = newEdge(v2, v1, weight)
	}
	// 如果本来没有边,边数量+1
	if !b {
		d.m++
	}
	return nil
}

// 判断v1,v2是否已经有边
func (d *weightedDenseGraph) HasEdge(v1, v2 int) (bool, error) {
	// 判断索引是否越界
	if v1 < 0 || v2 < 0 || v1 >= d.n || v2 >= d.n {
		return false, errors.New("index is illegal.")
	}
	return d.graph[v1][v2] != nil, nil
}

// 迭代器: 输出节点v所连接的节点,时间复杂度为O(n)
func (d *weightedDenseGraph) Iterator(v int) []*Edge {
	// 判断索引是否越界
	if v < 0 || v >= d.n {
		fmt.Println("index is illegal.")
		return nil
	}

	var buf []*Edge
	for _, j := range d.graph[v] {
		if j != nil {
			buf = append(buf, j)
		}
	}
	return buf
}

// 打印边
func PrintEdge(e []*Edge) {
	buf := make([]Edge, len(e))
	for i1, i2 := range e {
		if i2 != nil {
			buf[i1] = *i2
		}
	}
	fmt.Println(buf)
}

邻接表实现有权图
// 边类
type Edge struct {
	a      int     //a节点
	b      int     //b节点
	weight float64 //权值
}

func newEdge(a, b int, weight float64) *Edge {
	return &Edge{
		a:      a,
		b:      b,
		weight: weight,
	}
}

// 稀疏图 - 邻接表
type sparseGraph struct {
	n        int  // 节点数
	m        int  // 边数量
	directed bool //有向 or 无向图
	graph    [][]*Edge
}

func NewWeightSparseGraph(n int, directed bool) *sparseGraph {
	buf := make([][]*Edge, n)
	return &sparseGraph{
		n:        n,
		m:        0,
		directed: directed,
		graph:    buf,
	}
}

// 获取顶点数量
func (s *sparseGraph) GetVertex() int {
	return s.n
}

// 获取边数量
func (s *sparseGraph) GetEdge() int {
	return s.m
}

// 添加边: v1,v2均表示顶点相应的索引
func (s *sparseGraph) AddEdge(v1, v2 int, weight float64) error {
	// 判断索引是否越界
	if v1 < 0 || v2 < 0 || v1 >= s.n || v2 >= s.n {
		return errors.New("index is illegal.")
	}

	// 不处理平行边的情况
	s.graph[v1] = append(s.graph[v1], newEdge(v1, v2, weight))
	if v1 != v2 && !s.directed {
		s.graph[v2] = append(s.graph[v2], newEdge(v2, v1, weight))
	}
	s.m++
	return nil
}

// 判断v1,v2是否已经有边
func (s *sparseGraph) HasEdge(v1, v2 int) (bool, error) {
	// 判断索引是否越界
	if v1 < 0 || v2 < 0 || v1 >= s.n || v2 >= s.n {
		return false, errors.New("index is illegal.")
	}

	for _, v := range s.graph[v1] {
		if v.b == v2 {
			return true, nil
		}
	}
	return false, nil
}

// 迭代器: 输出节点v所连接的节点,时间复杂度为O(1)
func (s *sparseGraph) Iterator(v int) []*Edge {
	// 判断索引是否越界
	if v < 0 || v >= s.n {
		fmt.Println("index is illegal.")
		return nil
	}
	return s.graph[v]
}

func PrintEdge(e []*Edge) {
	buf := []Edge{}
	for _, i2 := range e {
		buf = append(buf, *i2)
	}
	fmt.Println(buf)
}

测试
func d_Test() {
	rand.Seed(time.Now().UnixNano())

	d := weightDenseGraph.NewWeightDenseGraph(10, false)
	for i := 0; i < 20; i++ {
		d.AddEdge(rand.Intn(10), rand.Intn(10), 0)
	}

	for i := 0; i < 10; i++ {
		a := d.Iterator(i)
		weightDenseGraph.PrintEdge(a)
	}
}

func s_Test() {
	rand.Seed(time.Now().UnixNano())

	d := weightSparseGraph1.NewWeightSparseGraph(10, false)
	for i := 0; i < 20; i++ {
		d.AddEdge(rand.Intn(10), rand.Intn(10), 0)
	}

	for i := 0; i < 10; i++ {
		a := d.Iterator(i)
		weightSparseGraph1.PrintEdge(a)
	}
}
func main() {
	fmt.Println("邻接表有权图")
	s_Test()
	fmt.Println("========")
	fmt.Println("邻接矩阵无权图")
	d_Test()
}

测试结果 //
邻接表有权图
[{0 4 0} {0 9 0} {0 4 0} {0 3 0} {0 9 0} {0 4 0}]
[{1 3 0} {1 1 0} {1 1 0} {1 4 0} {1 8 0} {1 7 0}]
[{2 8 0} {2 6 0}]
[{3 1 0} {3 0 0}]
[{4 7 0} {4 0 0} {4 0 0} {4 1 0} {4 0 0}]
[{5 8 0} {5 7 0}]
[{6 2 0} {6 8 0}]
[{7 4 0} {7 5 0} {7 1 0}]
[{8 2 0} {8 5 0} {8 9 0} {8 9 0} {8 1 0} {8 6 0}]
[{9 0 0} {9 8 0} {9 0 0} {9 8 0}]
========
邻接矩阵无权图
[{0 0 0} {0 1 0} {0 3 0} {0 7 0} {0 9 0}]
[{1 0 0} {1 3 0} {1 4 0} {1 7 0}]
[{2 9 0}]
[{3 0 0} {3 1 0} {3 4 0} {3 9 0}]
[{4 1 0} {4 3 0} {4 8 0}]
[{5 5 0} {5 9 0}]
[]
[{7 0 0} {7 1 0} {7 8 0}]
[{8 4 0} {8 7 0} {8 9 0}]
[{9 0 0} {9 2 0} {9 3 0} {9 5 0} {9 8 0}]

总结：邻接矩阵有序，邻接表无序，邻接矩阵遍历时间复杂度O(n)，邻接表遍时间复杂度O(1) //