golang 实现菜单树的生成,包括菜单节点的选中状态、半选中状态,菜单的搜索。
1 该包提供两个方法根接口
1.1 GenerateTree(nodes, selectedNodes []INode) (trees []Tree)
GenerateTree 自定义的结构体实现 INode 接口后调用此方法生成树结构。
1.2 FindRelationNode(nodes, allNodes []INode) (respNodes []INode)
FindRelationNode 在 allTree 中查询 nodes 中节点的所有父子节点 返回 respNodes(包含 nodes , 跟其所有父子节点)
1.3 接口 INode
// ConvertToINodeArray 其他的结构体想要生成菜单树,直接实现这个接口
type INode interface {
// GetTitle 获取显示名字
GetTitle() string
// GetId获取id
GetId() int
// GetFatherId 获取父id
GetFatherId() int
// GetData 获取附加数据
GetData() interface{}
// IsRoot 判断当前节点是否是顶层根节点
IsRoot() bool
}
2 使用
go get github.com/azhengyongqin/golang-tree-menu
2.1 定义自己的菜单结构体并且实现接口 INode
// 定义我们自己的菜单对象
type SystemMenu struct {
Id int `json:"id"` //id
FatherId int `json:"father_id"` //上级菜单id
Name string `json:"name"` //菜单名
Route string `json:"route"` //页面路径
Icon string `json:"icon"` //图标路径
}
func (s SystemMenu) GetTitle() string {
return s.Name
}
func (s SystemMenu) GetId() int {
return s.Id
}
func (s SystemMenu) GetFatherId() int {
return s.FatherId
}
func (s SystemMenu) GetData() interface{} {
return s
}
func (s SystemMenu) IsRoot() bool {
// 这里通过FatherId等于0 或者 FatherId等于自身Id表示顶层根节点
return s.FatherId == 0 || s.FatherId == s.Id
}
2.2 实现一个将自定义结构体SystemMenu 数组转换成 INode 数组的方法
type SystemMenus []SystemMenu
// ConvertToINodeArray 将当前数组转换成父类 INode 接口 数组
func (s SystemMenus) ConvertToINodeArray() (nodes []INode) {
for _, v := range s {
nodes = append(nodes, v)
}
return
}
3 测试效果
3.1 添加测试数据
// 模拟获取数据库中所有菜单,在其它所有的查询中,也是首先将数据库中所有数据查询出来放到数组中,
// 后面的遍历递归,都在这个 allMenu中进行,而不是在数据库中进行递归查询,减小数据库压力。
allMenu := []SystemMenu{
{Id: 1, FatherId: 0, Name: "系统总览", Route: "/systemOverview", Icon: "icon-system"},
{Id: 2, FatherId: 0, Name: "系统配置", Route: "/systemConfig", Icon: "icon-config"},
{Id: 3, FatherId: 1, Name: "资产", Route: "/asset", Icon: "icon-asset"},
{Id: 4, FatherId: 1, Name: "动环", Route: "/pe", Icon: "icon-pe"},
{Id: 5, FatherId: 2, Name: "菜单配置", Route: "/menuConfig", Icon: "icon-menu-config"},
{Id: 6, FatherId: 3, Name: "设备", Route: "/device", Icon: "icon-device"},
{Id: 7, FatherId: 3, Name: "机柜", Route: "/device", Icon: "icon-device"},
}
3.2 生成完全树
// 生成完全树 resp := GenerateTree(SystemMenus.ConvertToINodeArray(allMenu), nil) bytes, _ := json.MarshalIndent(resp, "", "\t") fmt.Println(string(bytes))
[
{
"title": "系统总览",
"leaf": false,
"checked": false,
"partial_selected": false,
"children": [
{
"title": "资产",
"leaf": false,
"checked": false,
"partial_selected": false,
"children": [
{
"title": "设备",
"leaf": true,
"checked": false,
"partial_selected": false,
"children": null
},
{
"title": "机柜",
"leaf": true,
"checked": false,
"partial_selected": false,
"children": null
}
]
},
{
"title": "动环",
"leaf": true,
"checked": false,
"partial_selected": false,
"children": null
}
]
},
{
"title": "系统配置",
"leaf": false,
"checked": false,
"partial_selected": false,
"children": [
{
"title": "菜单配置",
"leaf": true,
"checked": false,
"partial_selected": false,
"children": null
}
]
}
]

3.3 带选中状态和半选中状态的树
// 模拟选中 '资产' 菜单
selectedNode := []SystemMenu{allMenu[2]}
resp = GenerateTree(SystemMenus.ConvertToINodeArray(allMenu), SystemMenus.ConvertToINodeArray(selectedNode))
bytes, _ = json.Marshal(resp)
fmt.Println(string(pretty.Color(pretty.PrettyOptions(bytes, pretty.DefaultOptions), nil)))

[
{
"title": "系统总览",
"leaf": false,
"checked": false,
"partial_selected": true,
"children": [
{
"title": "资产",
"leaf": false,
"checked": true,
"partial_selected": false,
"children": [
{
"title": "设备",
"leaf": true,
"checked": true,
"partial_selected": false,
"children": null
},
{
"title": "机柜",
"leaf": true,
"checked": true,
"partial_selected": false,
"children": null
}
]
},
{
"title": "动环",
"leaf": true,
"checked": false,
"partial_selected": false,
"children": null
}
]
},
{
"title": "系统配置",
"leaf": false,
"checked": false,
"partial_selected": false,
"children": [
{
"title": "菜单配置",
"leaf": true,
"checked": false,
"partial_selected": false,
"children": null
}
]
}
]
3.4 模拟查询某个节点,然后生成树
// 模拟从数据库中查询出 '设备'
device := []SystemMenu{allMenu[5]}
// 查询 `设备` 的所有父节点
respNodes := FindRelationNode(SystemMenus.ConvertToINodeArray(device), SystemMenus.ConvertToINodeArray(allMenu))
resp = GenerateTree(respNodes, nil)
bytes, _ = json.Marshal(resp)
fmt.Println(string(pretty.Color(pretty.PrettyOptions(bytes, pretty.DefaultOptions), nil)))

[
{
"title": "系统总览",
"leaf": false,
"checked": false,
"partial_selected": false,
"children": [
{
"title": "资产",
"leaf": false,
"checked": false,
"partial_selected": false,
"children": [
{
"title": "设备",
"leaf": true,
"checked": false,
"partial_selected": false,
"children": null
}
]
}
]
}
]
补充:golang实现prim算法,计算最小生成树
1、题目描述
给定一个n个点m条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出impossible。
给定一张边带权的无向图G=(V, E),其中V表示图中点的集合,E表示图中边的集合,n=|V|,m=|E|。
由V中的全部n个顶点和E中n-1条边构成的无向连通子图被称为G的一棵生成树,其中边的权值之和最小的生成树被称为无向图G的最小生成树。
输入格式
第一行包含两个整数n和m。
接下来m行,每行包含三个整数u,v,w,表示点u和点v之间存在一条权值为w的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出impossible。
2、数据
数据范围
1≤n≤500,
1≤m≤105,
图中涉及边的边权的绝对值均不超过10000。
输入样例:
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例:
6
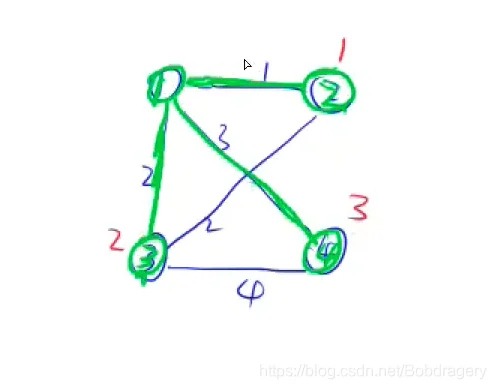
数据图
1、初始所有点的距离为正无穷,就是代码中的0x3f3f3f3f等于1061109567
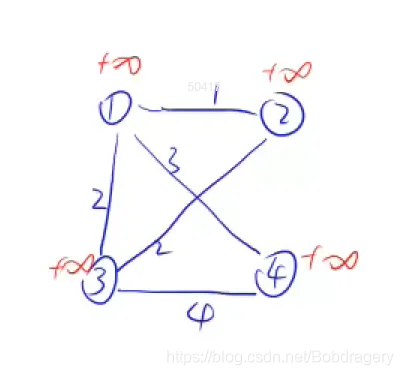
2、以第一个点为最初点,绿色表示选中,进入到最小生成树中
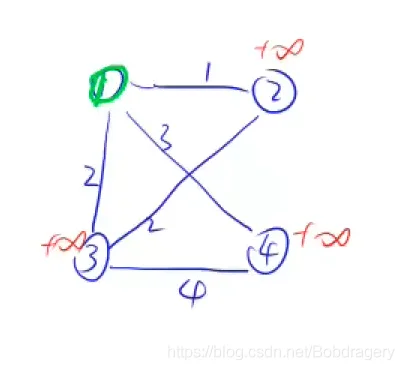
3、以第一个更新其他与之连通的点的距离
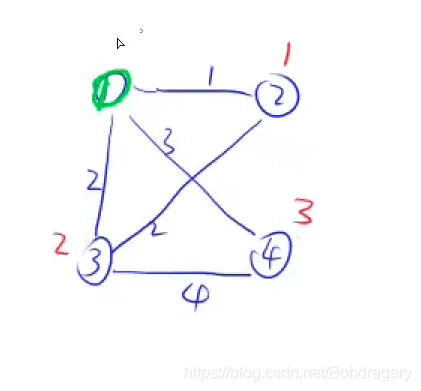
4、依次迭代 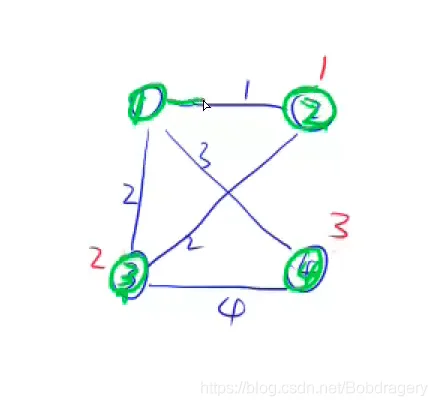
5、最后的最小生成树
3、朴素prim算法步骤时间复杂度O(n^2)
1、先初始化所有点距离为正无穷
2、迭代n次,依次用到集合的最小点更新剩余点距离
3、将已经确定的点加入到st集合中,st数组为一个bool类型
4、代码实现
/*
该图是稠密图,使用邻接矩阵
*/
package main
import (
"bufio"
"fmt"
"os"
"strconv"
"strings"
)
const (
N = 510
INF = 0x3f3f3f3f
)
var (
n, m int
dist [N]int
g [N][N]int
st [N]bool
)
func readLine(r *bufio.Reader) []int {
s, _ := r.ReadString('\n')
ss := strings.Fields(s)
res := make([]int, len(ss))
for i, v := range ss {
res[i], _ = strconv.Atoi(v)
}
return res
}
func prim() int {
// 初始化距离集合 dist
for i := 0; i < N; i++ {
dist[i] = 0x3f3f3f3f
}
// 迭代n次
res := 0 //res 存储最小生成树的大小即边的长度总和
for i := 0; i < n; i++ {
// 找到集合外距离最短的点
t := -1
for j := 1; j <= n; j++ {
if !st[j] && (t == -1 || dist[t] > dist[j]) {
t = j
}
}
// 迭代结束,此时的t就是距离最小点
// 情况一:图上的点不连通,不能组成最小生成树
if i > 0 && dist[t] == INF {
return INF
} // 如果不是第一个点并且最小店的距离是正无穷,则表示图是不连通的
if i > 0 {
res += dist[t]
} // 如果不是第一个点,这个t就表示当前点到集合某一个点的最小距离
// 用最小距离点更新其他跟 "现阶段形成的生成树" 的最短距离,
//注意更新的顺序,自环是不应该被加到最小生成树,所以,为了避免自环加入最小生成树,提前更新res
for j := 1; j <= n; j++ {
dist[j] = min(dist[j], g[t][j]) // 此步骤注意是dijkstra的区别,
}
st[t] = true
}
return res
}
func min(a, b int) int {
if a >= b {
return b
} else {
return a
}
}
func main() {
r := bufio.NewReader(os.Stdin)
input := readLine(r)
n, m = input[0], input[1]
//fmt.Scanf("%d%d\n", &n, &m)
// 初始化距离
for i := 0; i < N; i++ {
for j := 0; j < N; j++ {
if i == j {
g[i][j] = 0
} else {
g[i][j] = 0x3f3f3f3f
}
}
}
//
for m > 0 {
m--
in := readLine(r)
a, b, c := in[0], in[1], in[2] //输入
g[a][b] = min(g[a][b], c)
g[b][a] = g[a][b] // 无向图
}
t := prim()
if t == INF {
fmt.Println("impossible")
} else {
fmt.Println(t)
}
}
以上为个人经验,希望能给大家一个参考,也希望大家多多支持我们。如有错误或未考虑完全的地方,望不吝赐教。
