背景
计算机系统中经常会遇到这样一类问题:前一个任务已经执行完成,需要在待执行任务中挑选一个新的任务执行。最简单的方法就是将所有的任务排成一个队列,按照队列的先进先出(FIFO)的策略挑选要执行的任务。这种策略虽然保证了所有的任务都能被执行,但是往往会导致执行时间短的或者紧急度高的任务在队列中等待时间较长而导致效率低下。另一种策略是为每个任务安排一个优先级,每次挑选任务时只需要从队列中取出优先级最高的任务执行即可。实现该策略需要借助一种特殊的数据结构:优先级队列(PriorityQueue)。
优先级队列(PriorityQueue)
优先级队列虽然也叫队列,但是和普通的队列还是有差别的。普通队列出队顺序只取决于入队顺序,而优先级队列的出队顺序总是按照元素自身的优先级。换句话说,优先级队列是一个自动排序的队列。元素自身的优先级可以根据入队时间,也可以根据其他因素来确定,因此非常灵活。
优先级队列的内部实现有很多种,例如有序数组、无序数组和堆等。但是无论哪种实现,优先级队列必须实现以下两种方法:insert和delete。insert方法是将带优先级的元素插入优先级队列中(类似队列的enQueue方法);delete方法是从优先级队列中取出最高优先级(或最低优先级)的元素并在队列中删除该元素(类似队列的出队)。
针对不同实现,优先级队列的插入和删除方法的效率是不同的。
有序数组
下面的代码展示了使用有序数组实现优先级队列的基本功能。
插入操作涉及对数组排序,因此是O(n)【只需要对一个元素进行排序】;而删除操作的复杂度是O(1)。
同样也可以使用无序数组实现:插入操作时直接将元素插入无序数组的尾部,删除操作需要对数组进行排序并挑出最大的元素。
算法复杂度如下表所示:
| 实现方式 | 插入操作时间复杂度 | 删除操作时间复杂度 |
|---|---|---|
| 有序数组 | O(n) | O(1) |
| 无序数组 | O(1) | O(n) |
所以,无序数组可以认为是优先级队列(有序数组实现版)的惰性实现:直到要吐数据时再排序。
下面介绍一种特殊的数据结构-堆,可以提高优先级队列的性能。
堆
堆的定义
一般情况下,堆指的是二叉堆,而二叉堆是一棵完全二叉树,树中每个节点存储一个元素,并且具有以下性质:
- 树中所有元素都小于(或大于)它的所有后裔,最小(或最大)的元素是根元素【也叫堆序性】;
- 堆总是一棵完全树,即除了最底层,其他层的节点都被元素填满,且最底层尽可能地从左到右填入。
所以堆必须是具有堆序性的完全二叉树。
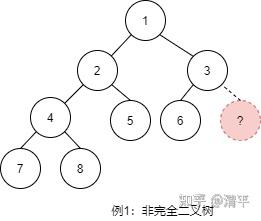

以上两个例子中的数据结构都不是堆。例1中的树是非完全二叉树;例2中的树虽然是完全二叉树,但是不具备堆序性。
根节点最大的堆叫大根堆,根节点最小的堆是小根堆。为了方便,下面以小根堆为例进行讨论(大根堆实际上也一样)。
堆的实现
存储结构
为了效率,二叉堆一般使用数组作为内部存储结构。将逻辑上的完全二叉树映射到一维数组中,数组中第一个元素存储树的根元素。为了方便,我们假设数据下标为0的位置不存储元素,从下标为1的位置开始,如图所示:
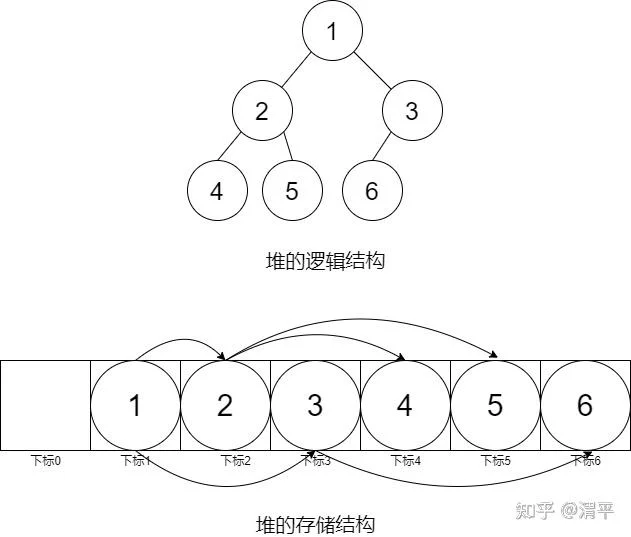
图中是一个包含6个元素的小根堆,上半部分是树状的逻辑表示,下半部分是该小根堆在数组中存储结构。数组中下标为k的元素的父节点(假设存在的话)的下标为[k/2](向下取整),其子节点(假设子节点存在)的下标为2k和2k+1。
算法实现(用Golang实现)
根据上面的讨论,我们使用数组来实现堆的内部存储结构:
实现堆的数据结构分为以下几个步骤:
- 实现最关键的插入和删除操作;
- 实现其他可选操作:如Peek()等方法;
- 实现堆的初始化操作。
插入和删除操作
插入操作:
向堆中插入一个元素,并且仍需保持堆的有序性。暴力方式是遍历堆的结构找到元素应该插入的位置后插入,但是该方式需要保证树的完全性和堆序性,效率低下。因此使用另外一个思路:直接将元素追加到树的尾部(此时保证树是完全二叉树),然后使用上浮操作将插入的元素上浮到合适的位置以保证堆序性。
上浮操作就是递归比较元素和其父节点的大小:如果元素比父节点小,则交换元素和父节点;如果元素比父节点大,则不做任何操作。如此循环直到元素找到合适的位置,或者插入元素已经换到根元素的位置。
具体过程如图所示:
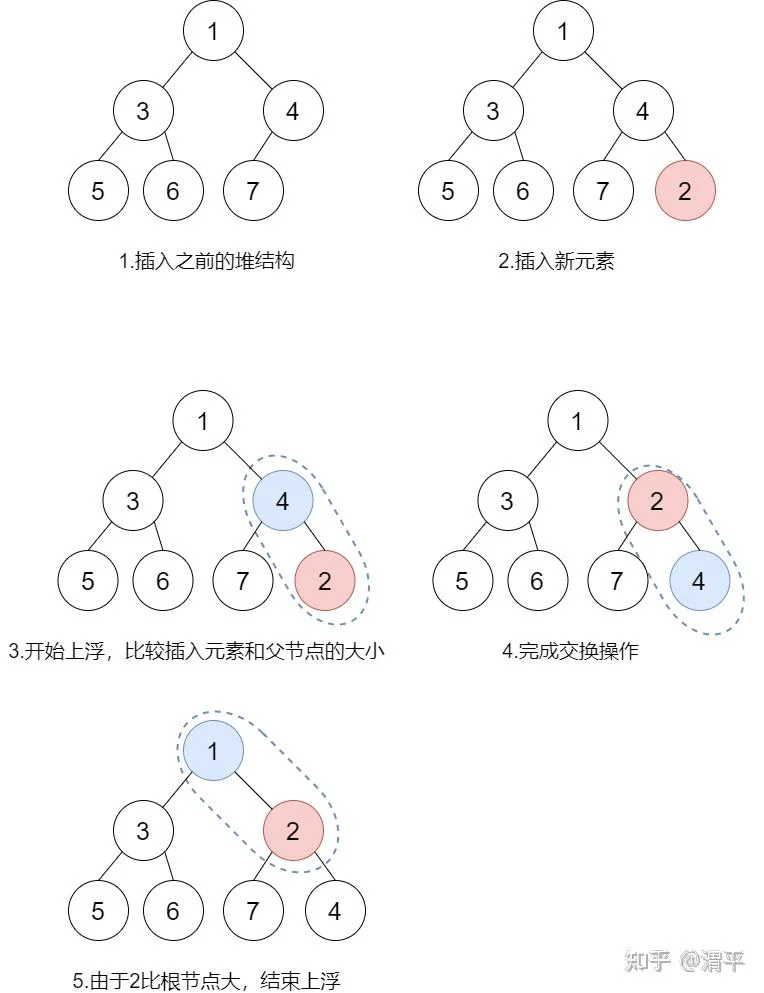
代码实现:
复杂度分析:插入操作的复杂度主要取决于上浮操作执行的次数,最差的情况下需要执行log(n)次【n为堆中元素个数,log(n)即为堆的高度】。因此插入操作的算法复杂度为O(log(n))。
删除操作:
删除操作是将堆中最小的元素从堆结构中删除,并返回该元素。由于根元素已经是堆中最小的元素,因此直接将根元素从堆中删除并返回根元素即可。但是具体实现有两种方法:
- 直接从堆中删除根节点,然后将两个子堆合并成新堆;
- 将根元素和堆中最后一个元素互换位置,然后删除最后一个元素,并对堆中新的元素执行下沉操作直到合适的位置。
由于合并两个堆的算法比较复杂,因此选择第二种方法实现删除操作。具体过程如下图所示:
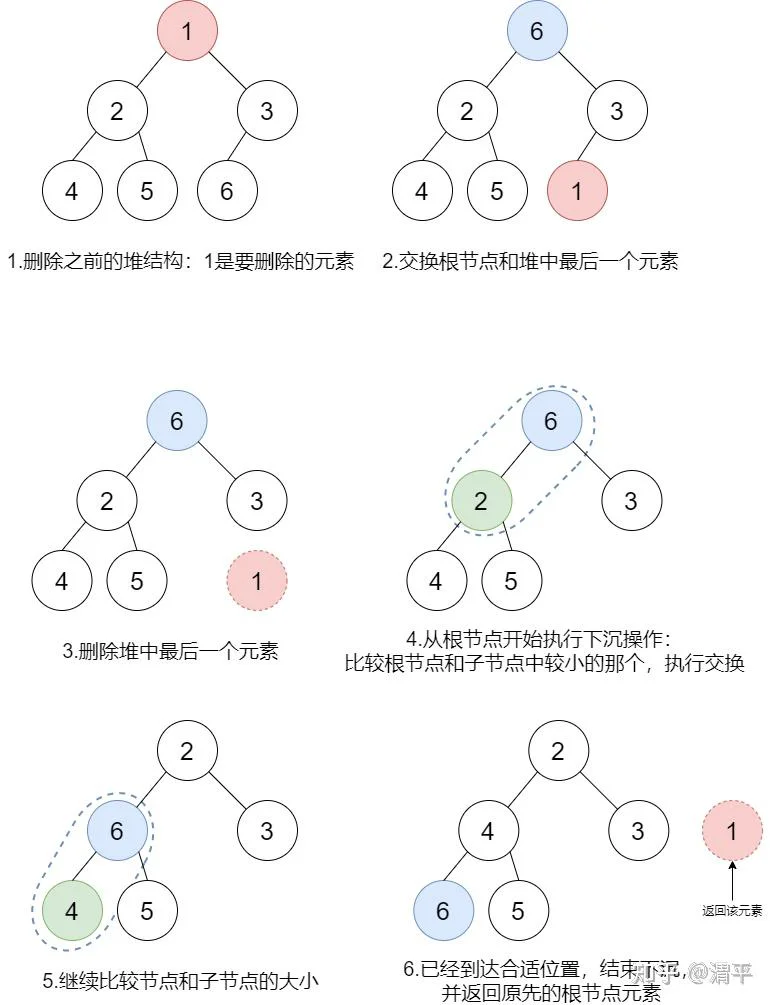
代码实现如下:
复杂度分析:删除操作的复杂度主要取决于下沉操作执行的次数,最差的情况下也是需要执行log(n)次。因此删除操作的算法复杂度为O(log(n))。
其他辅助函数
获取堆的大小
获取堆顶元素
删除特定元素
堆的初始化
现在我们来讨论以下堆的初始化。堆的初始化即如何从给定的数组中构造出一个堆来。这里有三种方法。
最简单的就是构造一个空堆,然后遍历数组,将数组元素不断添加到这个空堆中。空间复杂度为2个数组长度,时间复杂度为O(n*log(n))。因为每次向堆中插入时的复杂度为O(log(n)),总共有n次迭代。
第二种方法就是不是新的空堆,直接将原数组当作一个完全二叉树,然后从数组左侧开始不停执行上浮操作,直至遍历完整个数组。该方法直接在原数组上执行,因此空间复杂度为1个数组长度,时间复杂度仍为O(n*log(n))。过程如下图所示:
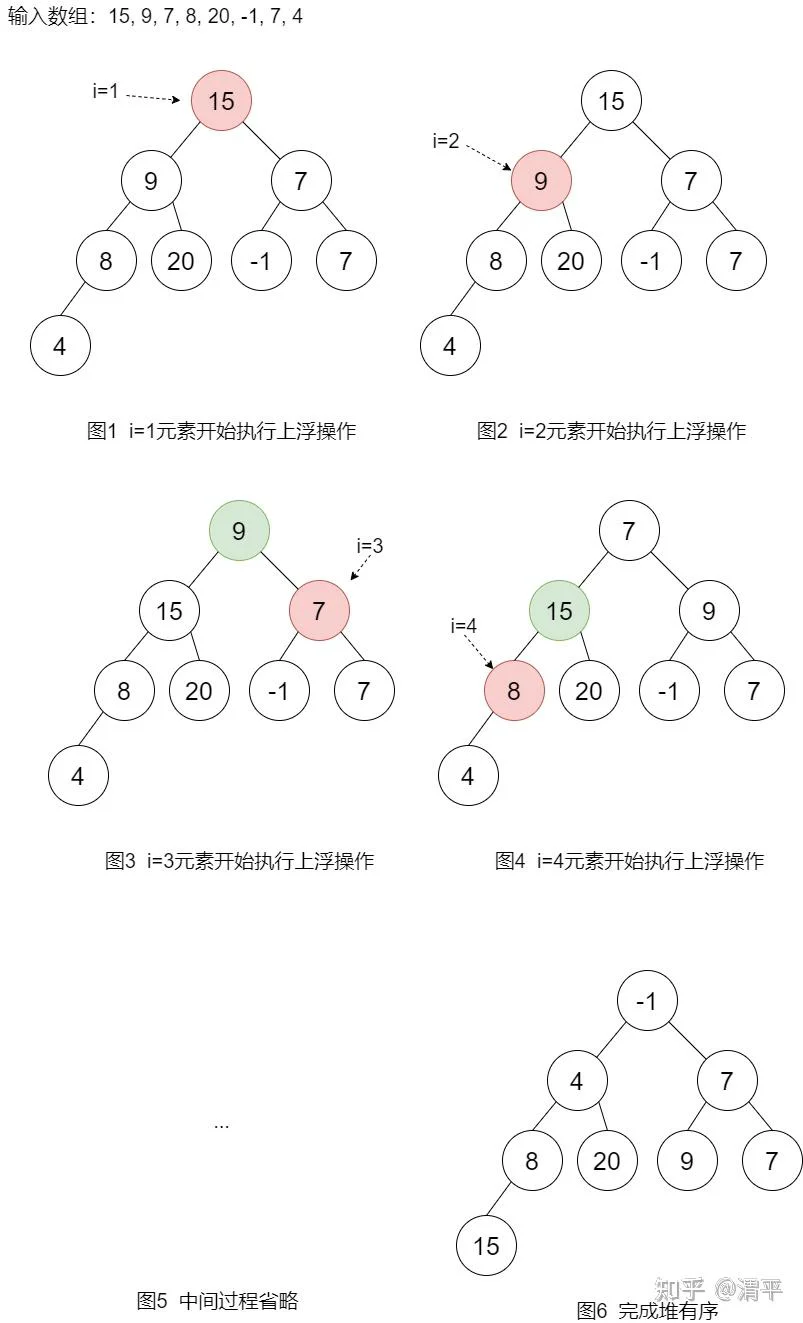
第三种方法:从数组的右侧开始不停执行下沉操作直至遍历至数组左侧为止。该方法的基本思想是若一棵树的左右两个子树已经是堆序状态了,那对整棵树只需要做一次根节点和左右两子树的根节点之间的修复操作即可保证整棵树都是堆有序的。同时对于叶子节点,只有其本身无需做修复操作,故可以只需要对数组中的一半元素执行下沉操作即可。过程如下图所示:
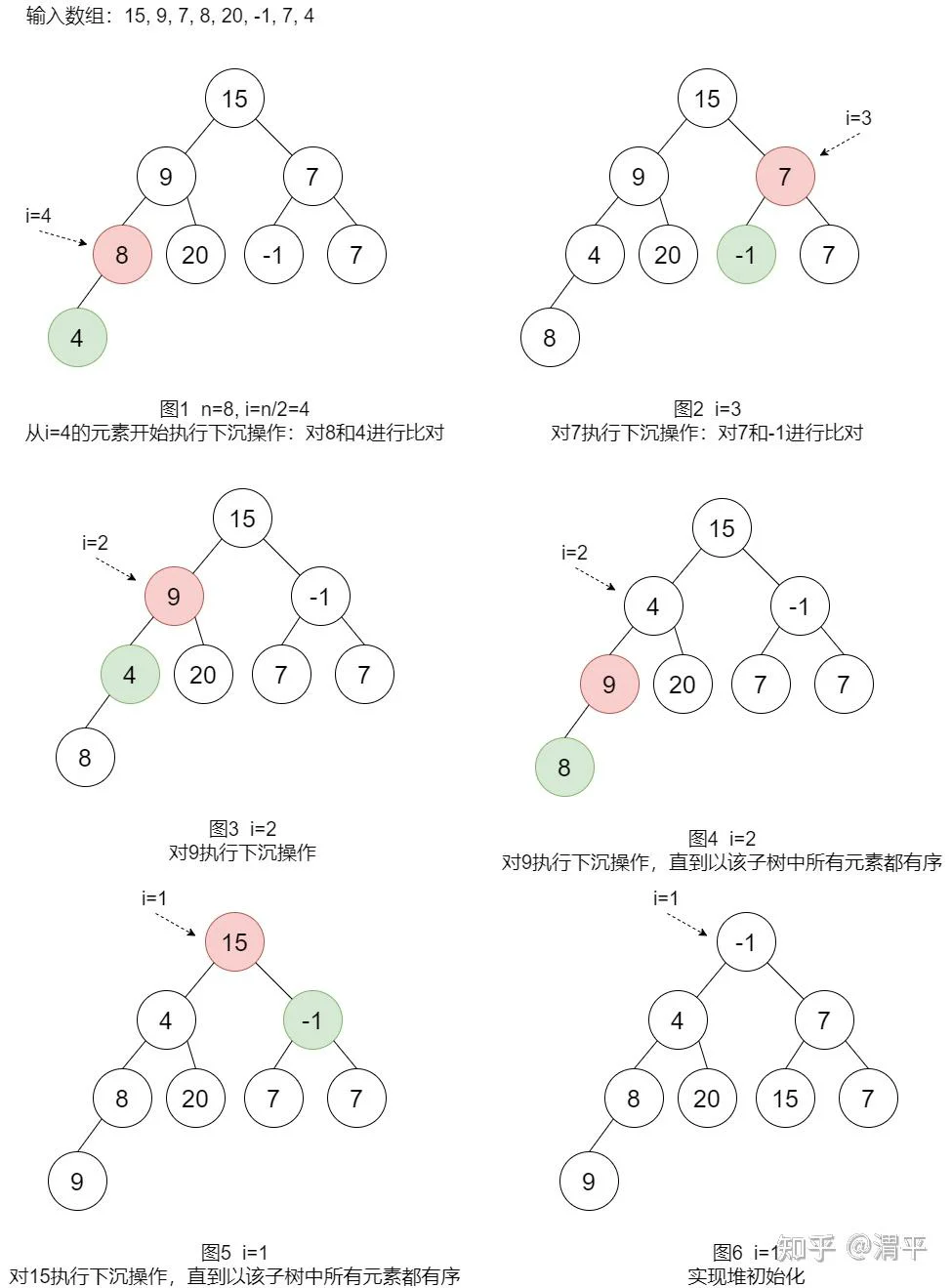
该方法也成为筛选方法,其算法复杂度:空间复杂度为1个数组长度,时间复杂度为O(N)。确实要比插入方法优秀。
算法复杂度
根据上面的介绍堆的相关复杂度如下表所示:
| 操作实现方式 | 空间复杂度 | 时间复杂度 |
|---|---|---|
| 堆初始化筛选 | n | O(log(n)) |
| 堆插入操作 | - | O(log(n)) |
| 堆删除操作 | - | O(log(n)) |
| 堆Peek方法 | - | O(1) |
