关于Pytorch框架下报错CUDA驱动版本不满足CUDA运行版本——一种可能的原因及解决办法

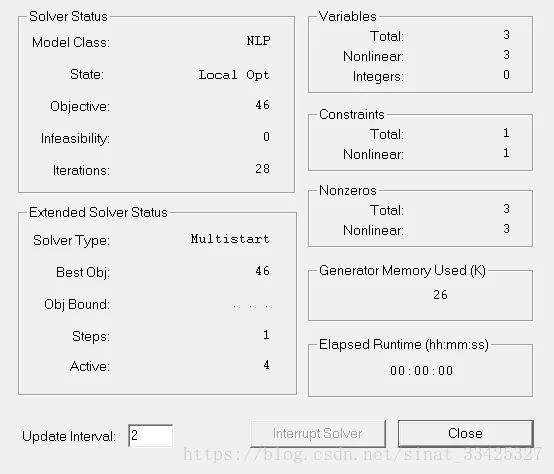
Solver status:求解器(求解程序)状态框

Model Class:当前模型的类型:LP，QP，ILP，IQP，PILP，PIQP，NLP，INLP，PINLP（以I开头表示IP，以PI开头表示PIP）

State:当前解的状态: "Global Optimum", "LocalOptimum", "Feasible", "Infeasible“(不可行), "Unbounded“(无界), "Interrupted“(中断), "Undetermined“(未确定)

Object:解的目标函数值

Infeasibility:当前约束不满足的总量(不是不满足的约束的个数):实数（即使该值=0，当前解也可能不可行，因为这个量中没有考虑用上下界命令形式给出的约束）

Iteration:目前为止的迭代次数

 

 

Extend solver status:扩展的求解器(求解程序)状态框

Solver type:使用的特殊求解程序:

Best obj :目前为止找到的可行解的最佳目标函数值

Objbound:目标函数值的界

Steps:特殊求解程序当前运行步数：

Active:有效步数

 

 

Variables（变量数量）：

  变量总数（Total）、

  非线性变量数（Nonlinear）、

  整数变量数（Integer）。

Constraints（约束数量）：

  约束总数（Total）、

  非线性约束个数(Nonlinear)。

Nonzeros（非零系数数量）：

 总数（Total）、

 非线性项系数个数(Nonlinear)。

 

GeneratorMemory Used (K) (内存使用量)

ElapsedRuntime (hh:mm:ss)（求解花费的时间）

 

代码格式：

model:

sets:
!此处为集合定义;
endsets

data:
!此处为数据导入;
enddata

calc:
！此处为计算段，专职已知数据的计算处理，不能含有变量;
endcalc

min\max=....;  !目标函数;
@for(....);   !约束条件;
...

end

注意事项

1. Lingo中默认所有的变量都是非负的，在程序中不需要写出相应的约束
2. 使用集合的方式定义向量，必须先定义，而标量不需要定义，直接使用即可
3. 三个要素条件：目标函数、决策变量、约束条件
4. 一个语句可以分几行输入，但必须使用英文分号结束
5. 注释使用！开始，英文分号结束
6. 变量不区分大小写
7. 所有函数以@开头

函数与运算符

Lingo具有９种逻辑运算符

‘#not#’ 否定该操作数的逻辑值，’＃not＃’是一个一元运算符。 
‘#eq# ’ 若两个运算数相等，则为 true；否则为 false。 
‘#ne#’ 若两个运算符不相等，则为 true；否则为 false。 
‘#gt#’ 若左边的运算符严格大于右边的运算符，则为 true；否则为 false。 
‘#ge#’ 若左边的运算符大于或等于右边的运算符，则为 true；否则为 false。 
‘#lt#’ 若左边的运算符严格小于右边的运算符，则为 true；否则为 false。 
‘#le#’ 若左边的运算符小于或等于右边的运算符，则为 true；否则为 false。 
‘#and# ’ 仅当两个参数都为 true 时，结果为 true；否则为 false。 
‘#or#’ 仅当两个参数都为 false 时，结果为 false；否则为 true。

集循环函数

@for：该函数用来产生对集成员的约束。 
@sum：该函数返回遍历指定的集成员的一个表达式的和。 
@min和@max：返回指定的集成员的一个表达式的最小值或最大值。

Lingo提供了大量的标准数学函数

@abs(x)返回 x 的绝对值。 
@sin(x)返回 x 的正弦值，x 采用弧度制。 
@cos(x)返回 x 的余弦值。 
@tan(x)返回 x 的正切值。 
@exp(x)返回常数 e 的 x 次方。 
@log(x)返回 x 的自然对数。 
@lgm(x)返回 x 的 gamma 函数的自然对数。 
@mod(x,y)返回 x 除以 y的余数。 
@sign(x)如果 x<0 返回-1；否则，返回 1。 
@floor(x)返回 x的整数部分。当 x>=0 时，返回不超过 x 的最大整数；当 x<0 时，返回 不低于 x 的最大整数。 
@smax(x1,x2,…,xn)返回 x1，x2，…，xn中的最大值。 
@smin(x1,x2,…,xn)返回 x1，x2，…，xn中的最小值。

变量界定函数实现对变量取值范围的附加限制，共 4种

@bin(x)限制 x 为 0 或1； 
@bnd(L,x,U)限制 L≤x≤U； 
@free(x)取消对变量 x的默认下界为 0 的限制，即x可以取任意实数； 
@gin(x)限制 x 为整数。

文件输入函数

@FILE(filename)：当前模型引用其他ASCII码文件中的数据或文本时可以采用此函数。用 ‘~’来隔开数据。

@OLE(filename，区间)：打开excel，输入数据

 

实例

线性规划

model:
sets:
!集合名称/成员变量/属性;
    warehouse/1..6/:e; 
    vendors/1..8/:d;
!派生集合名称（集合名称1、2）：属性;
    links(warehouse,vendors):c,x;
endsets

data:
!属性=数据列表;
!程序与数据在同一文件 
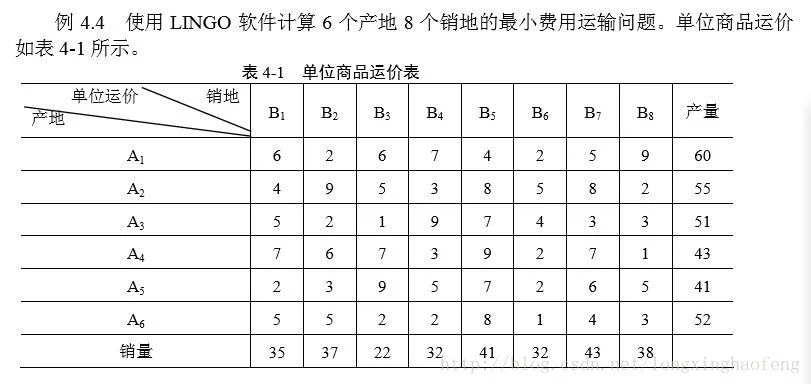
    e=60 55 51 43 41 52
    d=35 37 22 32 41 32 43 38
    c=6 2 6 7 4 2 9 5
      4 9 5 3 8 5 8 2
      5 2 1 9 7 4 3 3
      7 6 7 3 9 2 7 1
      2 3 9 5 7 2 6 5
      5 5 2 2 8 1 4 3;

!通过纯文本文件传递数据;
e=@file(sdata.txt);
e=@file(sdata.txt);
e=@file(sdata.txt);
@text(sdata2.txt)=@table(x);!将计算结果以表格形式输出文本文件;
!sdata.txt文本文件内容
 60 55 51 43 41 52~    
 35 37 22 32 41 32 43 38~
 6 2 6 7 4 2 9 5
 4 9 5 3 8 5 8 2
 5 2 1 9 7 4 3 3
 7 6 7 3 9 2 7 1
 2 3 9 5 7 2 6 5
 5 5 2 2 8 1 4 3;!~是记录分隔符;
enddata

!目标函数;
    min=@sum(links:c*x);
!需求约束;
    @for(vendors(J):@sum(warehouse(I):x(I,J))=d(J));
!产量约束;
    @for(warehouse(I):@sum(vendors(J):x(I,J))<=e(I));
!数据;

end

---

0-1整数规划

model: 
sets: 
num/1..10/:x0,y0,x;
link(num,num):y,d;
endsets 
data: 
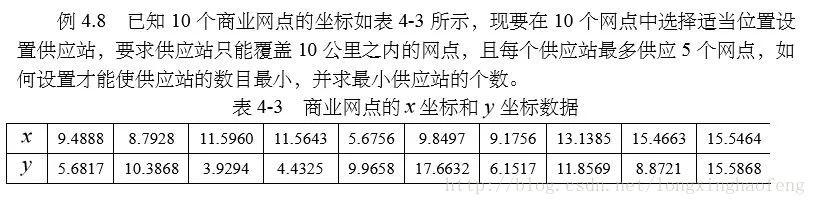
x0=9.4888 8.7928 11.5960 11.5643 5.6756 9.8497 9.1756 13.1385 15.4663 15.5464; 
y0=5.6817 10.3868 3.9294 4.4325 9.9658 17.6632 6.1517 11.8569 8.8721 15.5868; 
enddata 

calc:
@for(link(i,j):d(i,j)=@sqrt((x0(i)-x0(j))^2+(y0(i)-y0(j))^2));
endcalc

min=@sum(num:x);
@for(num(j):@sum(num(i):y(i,j))>=1);
@for(link(i,j):d(i,j)*y(i,j)<=10*x(i));
@for(link(i,j):x(i)>=y(i,j));
@for(num(i):@sum(num(j):y(i,j))<=5);
@for(link(i,j):@bin(y(i,j)));
@for(num(i):@bin(x(i)));
end

---

非线性拟合（最小二乘法）

model: 
sets: 
num/1..8/:x0,y0;

endsets 
data: 
x0=6 2 6 7 4 2 5 9; 
y0=4 9 5 3 8 5 8 2; 
enddata 

min=@sum(num:(y0-a/(@exp(b*x0)+c))^2);
@free(a);@free(b);@free(c);
end