- “>”(或“<”’)号与“>=”(或“<=”)功能相同
- Lingo中是不区分字母大小写的,必须以字母开头,可以包含数字和下划线
- LINGO程序中,只要定义好集合后,其他语句的顺序是任意的
- LINGO中的函数以“@”开头
- LINGO程序中默认所有变量都是非负的,数据部分不能使用分式
- LINGO中每一语句都必须要用一个英文状态下的分号结束,注释以英文状态的“!”开始,以英文状态下的“分号”结束,

线性规划的目标函数可以是求最大值,也可以是求最小值,约束条件的不等号可以是小于等于号也可以是大于等于号。为避免形式多样性带来的不便,Matlab中规定线性规划的标准形式为:

以下例子以该线性规划为基础:
目标函数:
m
a
x
z
=
2
x
1
+
3
x
2
−
5
x
3
max z = 2{x_1} + 3x{}_2 - 5{x_3}
maxz=2x1+3x2−5x3
约束条件:
x
1
+
x
2
+
x
3
=
7
{x_1} + {x_2} + {x_3} = 7
x1+x2+x3=7,
2
x
1
−
5
x
2
+
x
3
≥
10
2{x_1} - 5{x_2} + {x_3} \ge 10
2x1−5x2+x3≥10,
x
1
+
3
x
2
+
x
3
≤
12
{x_1} + 3{x_2} + {x_3} \le 12
x1+3x2+x3≤12,
x
1
,
x
2
,
x
3
≥
0
{x_1},{x_2},{x_3} \ge 0
x1,x2,x3≥0
化为Matlab标准型(使用MATLAB求解时必须化为标准型,Lingo求解则不作要求):
目标函数:
m
i
n
w
=
−
2
x
1
−
3
x
2
+
5
x
3
min w = -2{x_1} -3x{_2} +5{x_3}
minw=−2x1−3x2+5x3
约束条件:
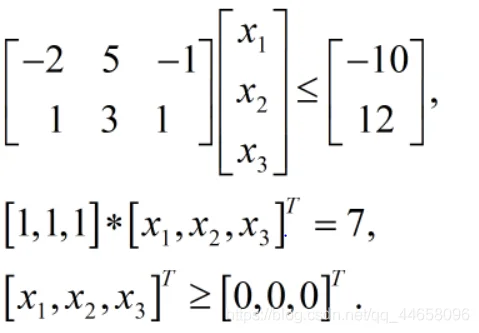
1.1 集合
集合部分语法为:
sets:
集合名称1/成员列表1/:属性1_1,属性1_2,…,属性1_n1;
集合名称2/成员列表2/:属性2_1,属性2_2,…,属性2_n2;
派生集合名称(集合名称1,集合名称2):属性3_1,…,属性3_n3;
endsets
例:
sets:
row/1..2/:b;
col/1..3/:c,x;
links(row,col):a;
endsets
1.2 数据
数据部分的语法为:
data:
属性1=数据列表
属性2=数据列表
enddata
例:
data:
c=2 3 -5;
a= -2 5 -1 1 3 1;
b= -10 12;
enddata
1.3 算术运算符
^ 乘方 * 乘 / 除 + 加 -减
1.4 变量界定函数
变量界定函数实现对变量取值范围的附加限制,共4种:
@bin(x) 限制x为0或1;
@bnd(L,x,U) 限制 L≤x≤U;
@free(x)取消对x的默认下界为0的限制,即x可以取任意实数;
@gin(x)限制x为整数;
1.5 集循环函数
@for : 该函数用来产生对集成员的约束。
@sum : 该函数返回遍历指定的集成员的一个表达式的和。
@min 和 @max:返回指定的集成员的一个表达式的最小值或最大值。
max=@ sum(col:c*x);
@for(row(i):@sum(col(j):a(i,j)*x(j))<b(i));
@sum(col:x)=7;
end
求得最优解为 x 1 = 6.4286 , x 2 = 0.5714 , x 3 = 0 , {x_1} = 6.4286,{x_2} = 0.5714,{x_3} = 0, x1=6.4286,x2=0.5714,x3=0,对应的最优值为 z=14.5714.
