Lingo 与计算机本地文件之间的数据传递

运算符

关系运算符

Lingo 仅识别 "=",">=","<="三种运算符

算术运算符

就是 + - 啥的

逻辑运算符

#eq#  !相等;
#ne#  !不相等;
#gt#  
#ge#
#lt#
#le#

#not#
#and#
#or#

例

内置函数概览

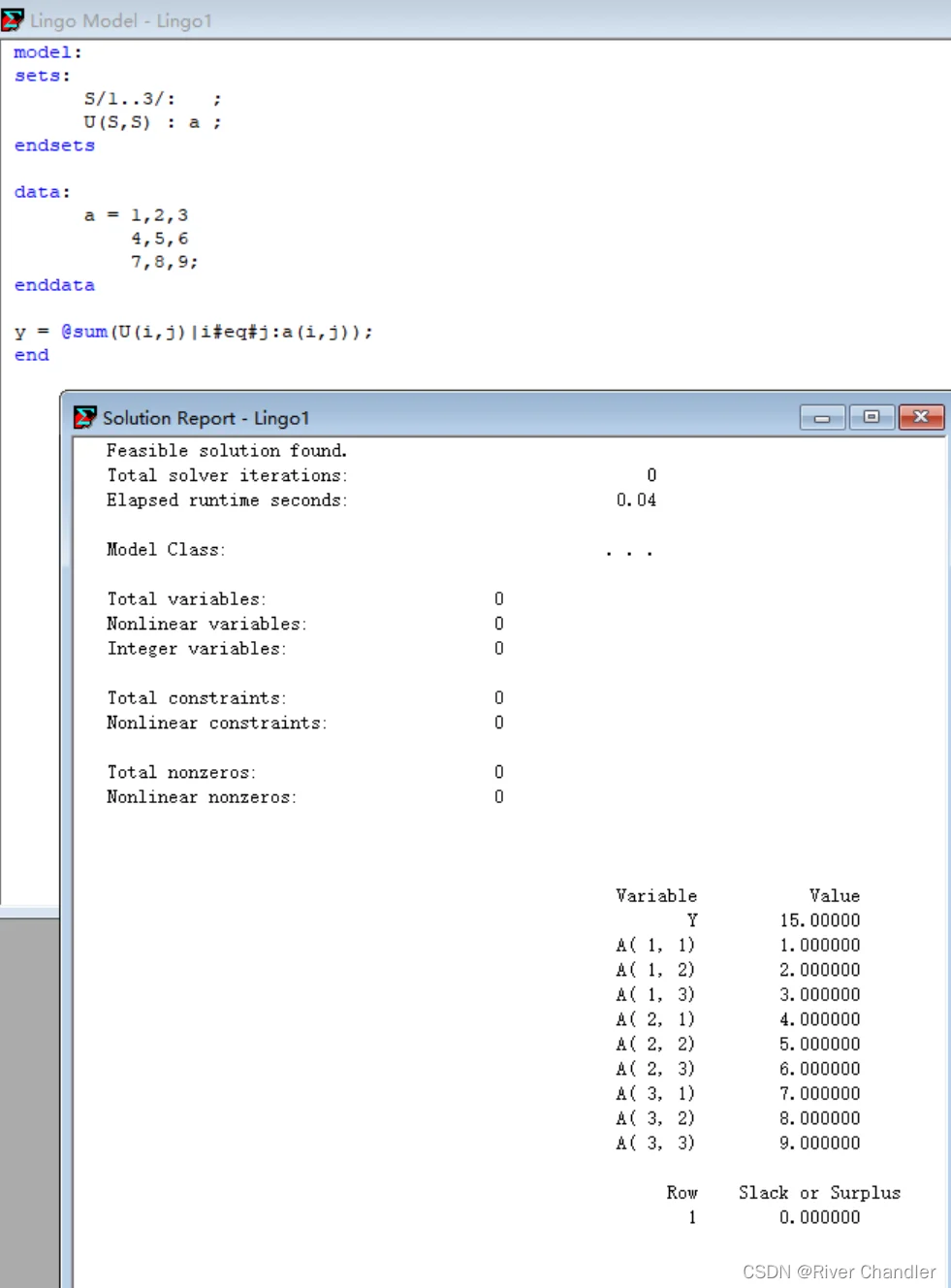
初等函数

@sin(x);
@cos(x);
@tan(x);
@log(x) ! x的自然对数值，其他应当使用换底公式;
@exp(x);

边界函数

@bin(x)     !x为0或者1;
@gin(x)     !x为整数;
@free(x)    !x为任意实数;
@bnd(v,x,u) !x的取值区间
！lingo 默认变量为非负实数

集合函数

@for
@sum
@prod
@max
@min
@in
@size

分支结构设计

例子

小规模线性计算

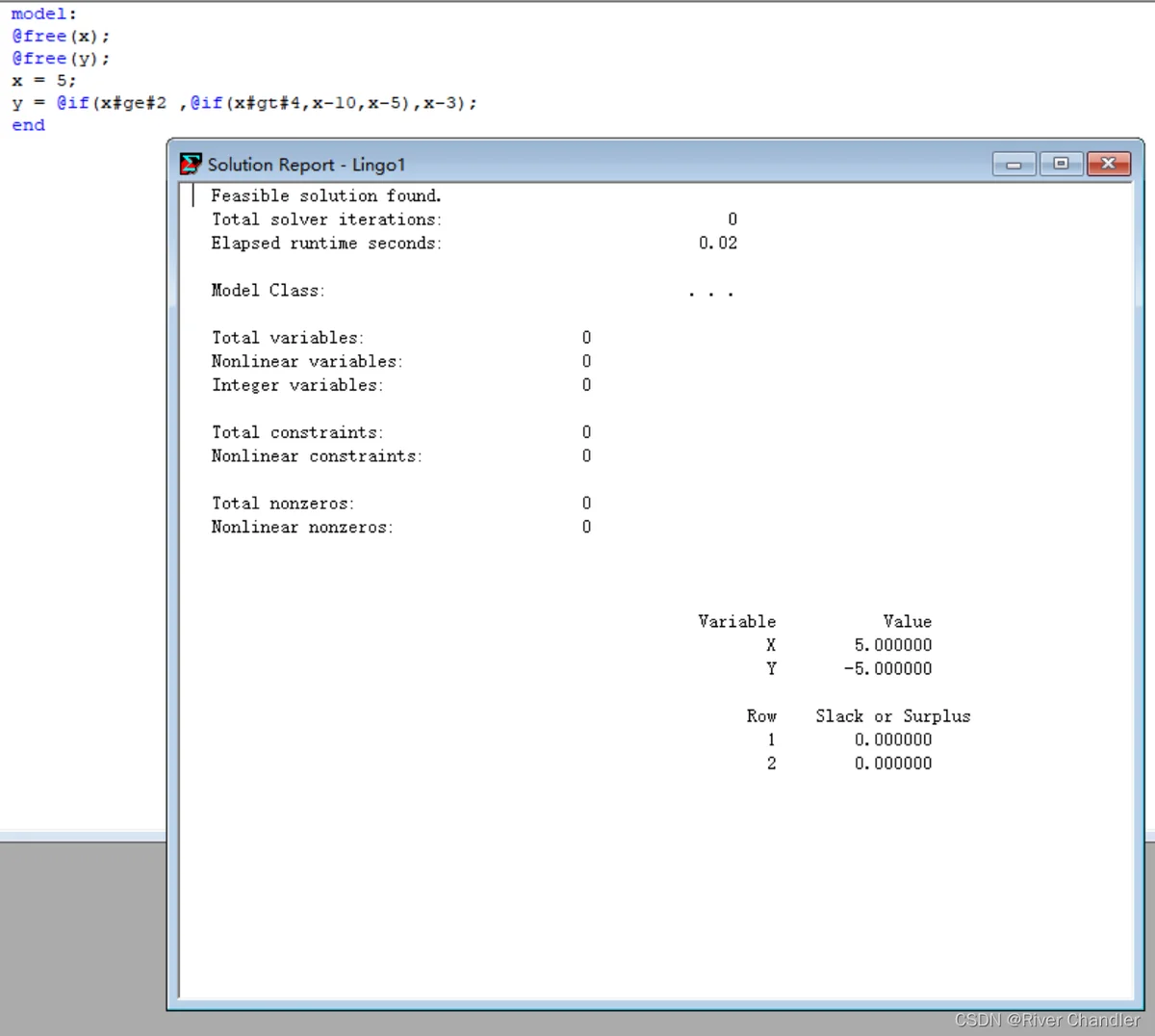
例

max = x1 + 2*x2 + x3;
	x1 > x2;
	x1 +      x2 <= 5;
	x1 +      x3 >= 2;
@bin(x3);
@gin(x2);
@bnd(2,x1,10);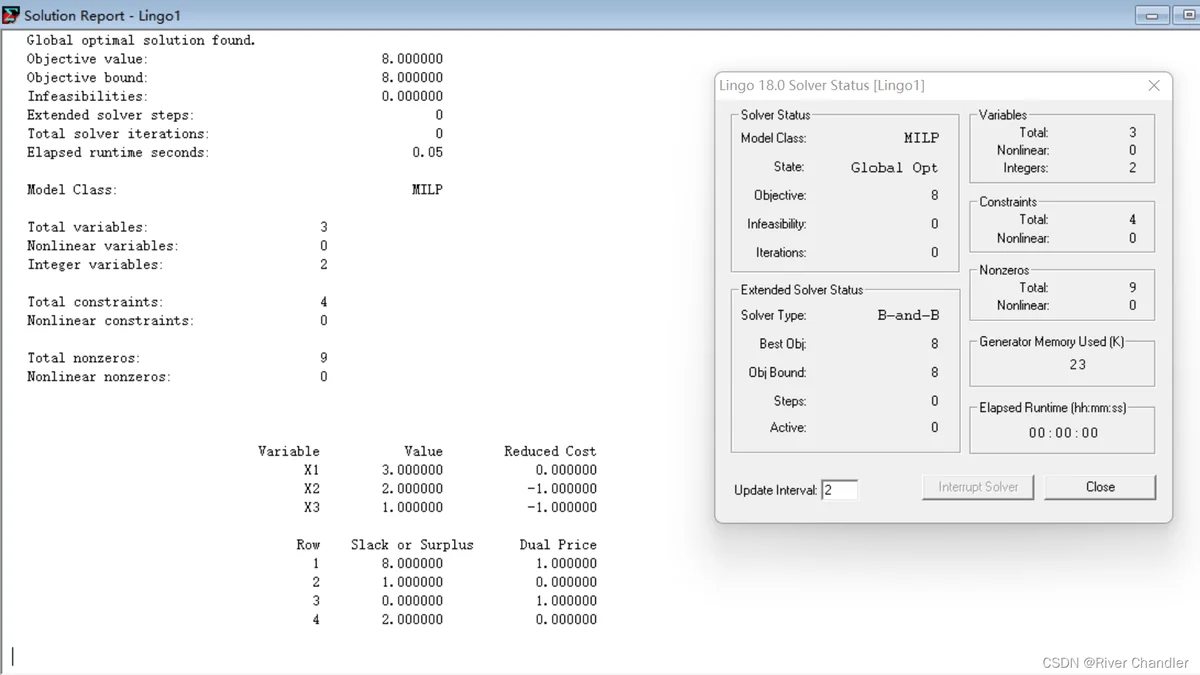

大规模线性计算

例

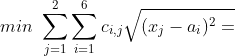
$min\,\,\sum_{j=1}^{2}\sum_{i=1}^{6}c_{i,j}\sqrt{(x_j-a_i)^2+(y_j-b_i)^2}$

s.t.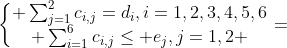 $\left\{\begin{matrix} \sum_{j=1}^{2}c_{i,j}=d_i,i=1,2,3,4,5,6\\ \sum_{i=1}^{6}c_{i,j}\leq e_j,j=1,2 \end{matrix}\right.$

sets:
s/1..6/: a,b,d;
T/1..2/: e,x,y;
U(S,T):  c;
endsets

data:
a = 1.25 8.75 0.5  5.75 3    7.25;
b = 1.25 0.75 4.75 5    6.5  7.25;
d = 3    5    4    7    6    11;
x = 5 2;
y = 1 7;
e = 20 20;
enddata

min = @sum(T(j):@sum(S(i):
	c(i,j)*@sqrt((x(j)-a(i))^2+(y(j)-b(i))^2)));
@for(S(i):
	@sum(T(j):c(i,j))=d(i));
@for(T(j):
	@sum(S(i):c(i,j))<=e(j));

实战--最短路径问题

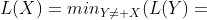
$L(X)=min_{Y\neq X}(L(Y)+d(Y,X))\,\,\,X\neq S$

model:
sets:
	cities/S,A1,A2,A3,B1,B2,C1,C2,T/:L;
	roads(cities,cities)/
	S,A1 S,A2 S,A3
	A1,B1 A1,B2 A2,B1 A2,B2 A3,B1 A3,B2
	B1,C1 B1,C2 B2,C1 B2,C2
	C1,T C2,T/:D;
endsets

data:
D = 	6,3,3
	6 5 8 6 7 4
      6 7 8 9
      5 6;

L = 0, , , , , , , , ;
enddata

@for(cities(i)|i#GT#@index(S):
L(i)=@min(roads(j,i):L(j)+D(j,i)););
end

                                                    Variable           Value
                                                       L( S)        0.000000
                                                      L( A1)        6.000000
                                                      L( A2)        3.000000
                                                      L( A3)        3.000000
                                                      L( B1)        10.00000
                                                      L( B2)        7.000000
                                                      L( C1)        15.00000
                                                      L( C2)        16.00000
                                                       L( T)        20.00000

非线性求解

打开全局求解器

Solver -> Options -> Global Solver -> tick "Use Global Solver" -> apply -> OK

非线性求解应该设置初值

例

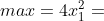
$max=4x_1^2+x_2*sin(x_3^{0.5})$

s.t. $\left\{\begin{matrix} x_1^2+x_3^3<=3\\ x_1^5>=x_2^2>=x_3^2 \end{matrix}\right.$

model:
init:
	x1 = 0.0;
	x2 = 0.0;
	x3 = 0.0;
endinit

max = 4*x1^2 + x2*@sin(@sqrt(x3));
	x1^3 + x3^3 <= 3;
	x1^5 - x2^2 >= 0;
	x2^2 - x3^2 >= 0;
end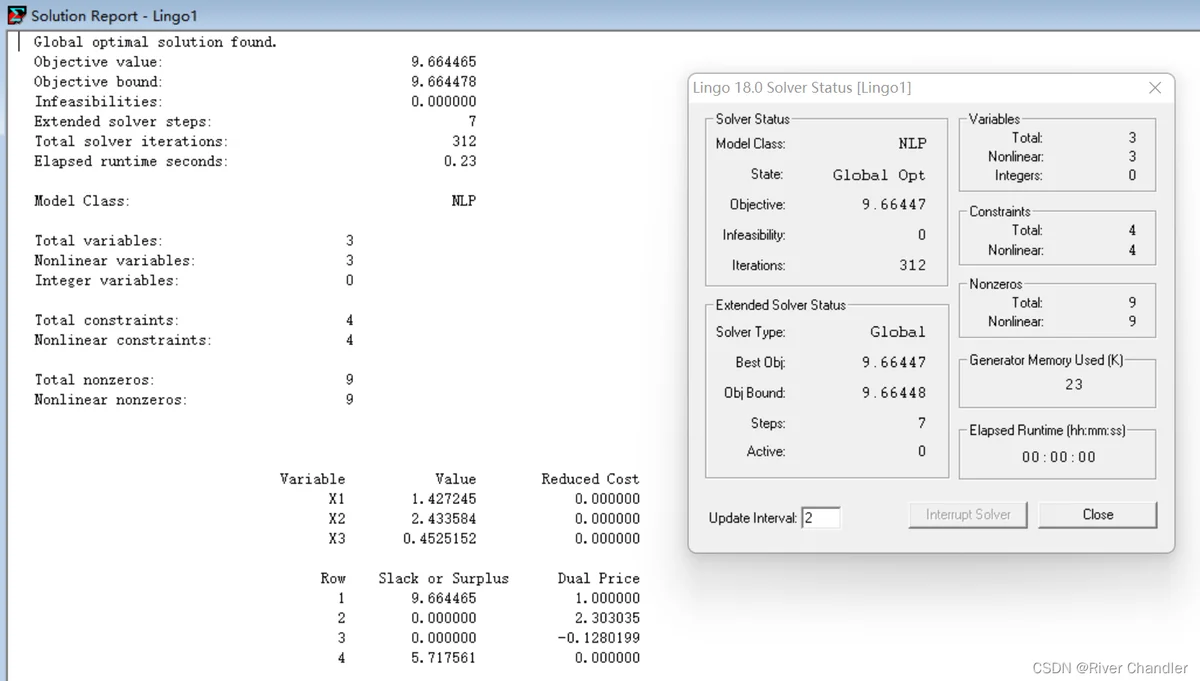

Lingo积分运算

早期Lingo版本不支持积分运算
现在Lingo-18的版本,支持了,但又没完全支持,你不能指望Lingo有着C++的速度做着Mathematical的事
Lingo积分只有一个命令,看上去就不像是能支持多元函数的

@INTEGRAL(y1,x,0,5,y);

Lingo积分的使用就有点鸡肋了,很复杂

MODEL:

PROCEDURE y1:
y = 4*x^3; 
ENDPROCEDURE

CALC:
PROB = @INTEGRAL(y1,x,0,5,y);
ENDCALC

END

@INTEGRAL 函数在实际问题中的表现

MODEL:

sets:
U/1..3/:a,b;
endsets

data:
a = 1,2,3;
enddata

PROCEDURE y1:
y = b(2)*x^3; 
ENDPROCEDURE

PROCEDURE y2:
y = b(1)*x^2;
ENDPROCEDURE

CALC:
PROB1 = @INTEGRAL(y1,x,0,5,y);
PROB2 = @INTEGRAL(y2,x,b(3),5,y);
ENDCALC

min = (PROB2-PROB1-(PROB2-b(3))^2)^b(1);
	@bnd(2,b(3),4);
	@bnd(1,b(2),4);
	@bnd(3,b(1),7);
END

解的报告

Local optimal solution found.
  Objective value:                            -0.1582482E+11
  Infeasibilities:                              0.000000
  Extended solver steps:                               1
  Best multistart solution found at step:              1
  Total solver iterations:                             4
  Elapsed runtime seconds:                          0.11

  Model Class:                                       NLP

  Total variables:                      4
  Nonlinear variables:                  2
  Integer variables:                    0

  Total constraints:                    1
  Nonlinear constraints:                1

  Total nonzeros:                       2
  Nonlinear nonzeros:                   2



                                Variable           Value        Reduced Cost
                                       Y        1.234568            0.000000
                                       X        1.234568            0.000000
                                   PROB1        192.9012            0.000000
                                   PROB2        50.66597            0.000000
                                   A( 1)        1.000000            0.000000
                                   A( 2)        2.000000            0.000000
                                   A( 3)        3.000000            0.000000
                                   B( 1)        3.000000            0.000000
                                   B( 2)        1.234568            0.000000
                                   B( 3)        2.000000           0.1840500E+10

                                     Row    Slack or Surplus      Dual Price
                                       1      -0.1582482E+11       -1.000000

别的不说,就运算速度而言,0.11s
绝对完爆其他计算软件与程序啊!!!!

Lingo 整数规划的多个解

Lingo 一般只会给出一个解,但对于整数规划来说,很可能会产生多个最优解
打开最优解控制器
- Solver >>> Integer Solver >>> K-Bset Solutions >>> Number
例:

model:
sets:
variables/1..10/:s,cost;
endsets

data:
cost=5 8 10 6 9 5 7 6 10 8;
enddata

min=@sum(variables(i):s(i)*cost(i));
(s(1)+s(7)-2)*(s(9)-1)=0;
s(3)*s(5)+s(4)*s(5)=0;
@sum(variables(i)|i#ge#5#and#i#le#8:s(i))<=2;
@sum(variables:s)=5;
@for(variables:@bin(s));
end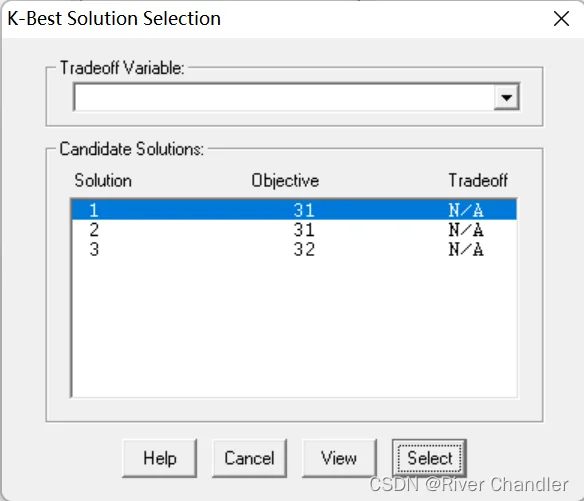

Lingo 解决数独问题 Lingo 与计算机本地文件之间的数据传递

我先在这里问候一下SB的某川大学的大学物理实验课！评价SX！评价完。

lingo数据文件

读取函数@file(fname);
写入函数@text(fname);
~~这个以后再说吧。反正小规模问题也遇不上，再说了，数据在excel里，你不是还得输入一边吗。当然不是。~~
读取函数是一行一行得读取的，至于一行一行的读取，那必然就需要你多次写入
- 希望这个时候你已经很好得理解了set语言了
很好，现在我们基本完成了我们所要初步掌握的做的全部操作

输出函数

输出函数@TEXT(["filename"])

示范样例

Model:
sets:
	myset/@file(myfile.ldt)/:@file(myfile.ldt);
endsets
	min = @sum(myset(i):ordered(i)*cost(i));
	@for(myset(i):ordered(i)>need(i);
	              ordered(i)<supply(i));
data:
	cost = @file(myfile.ldt);
	need = @file(myfile.ldt);
	supply = @file(myfile.ldt);

	@text("example.txt")=ordered;

enddata
end

其中myfile.lgt文件中的内容是

Seattle,Detroit,Chicago,Denver~
COST,NEED,SUPPLY,ORDERED~
12,28,15,20~
1600,1800,1200,1000~
1700,1900,1300,1100

这玩意它长这个样子

Lingo与excel的交互

这个就稍微复杂一点儿了。
需要宏的知识并在还需要再学习几个lingo的函数
很好，那就这样吧。

解的报告

Solver Status

Model Class

LP	线性模型
QP	二次模型
ILP	整数线性模型
IQP	整数二次模型
PILP	纯整数线性模型
PIQP	纯整数二次模型
NLP	非线性模型
或者还有其他的。。一些怪怪的模型

State

Global Optimum	全局最优
Local Optimum	局部最优
Feasible	可行的
Infeasible	不可行的
Unbounded	无界的
Interrupted
Undetermined

Objective
- max 或者 min 的值
Infeasibility
Interations
- 迭代次数
其他还有很多，但是我想也不是特别重要。。。

Solution Report

  Local optimal solution found.
  Objective value:                              37.00000
  Objective bound:                              37.00000
  Infeasibilities:                              0.000000
  Extended solver steps:                               3
  Total solver iterations:                            71
  Elapsed runtime seconds:                          0.18

  Model Class:                                      MIQP

  Total variables:                      3
  Nonlinear variables:                  2
  Integer variables:                    2

  Total constraints:                    2
  Nonlinear constraints:                2

  Total nonzeros:                       6
  Nonlinear nonzeros:                   2



                                Variable           Value        Reduced Cost
                                      X1        1.000000           -1.000000
                                      X2        4.000000           -9.000001
                                      X3        9.000000           -4.000000

                                     Row    Slack or Surplus      Dual Price
                                       1        37.00000            1.000000
                                       2        14.00000            0.000000

重点是
- Objective value
- Variable列

工具栏

Help

Register
- 非正版用户请忽略
Help topics
- 有全部的帮助文档

结果报告

Global optimal solution found.
- 全局最优解找到.
Objective value
- 最优目标值
Infeasibilities
- 指矛盾约束的个数
Total solver iterations
- 用单纯行法进行了两次迭代
Model Class
Total variables
Nonlinear variables
Integer variables
Total constraints
Nonlinear constraints
Total nonzeros
Nonlinear nonzeros

Variable

Value

Reduced Cost

Row Slack or Surplus Dual Price

变量

最优解中各变量的值

某个变量在解中的数值

增加一个单位，

目标函数值必须付出的代价

松弛变量,过剩变量

Lingo 与 计算机本地文件 之间的数据传递

关系运算符

算术运算符

逻辑运算符

例

初等函数

边界函数

集合函数

分支结构设计

例子

例

例

实战--最短路径问题

打开全局求解器

非线性求解应该设置初值

例

@INTEGRAL 函数在实际问题中的表现

解的报告

lingo数据文件

输出函数

示范样例

Lingo与excel的交互

Solver Status

Solution Report

Help

Lingo 与计算机本地文件之间的数据传递