一个最短路径问题
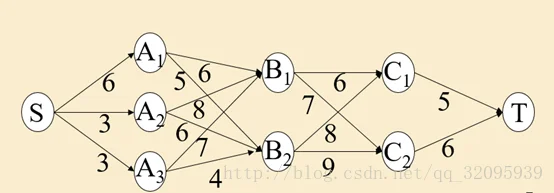
例 (最短路问题) 在纵横交错的公路网中,货车司机希望找到一条从一个城市到另一个城市的最短路. 下图表示的是公路网, 节点表示货车可以停靠的城市,弧上的权表示两个城市之间的距离(百公里). 那么,货车从城市S出发到达城市T,如何选择行驶路线,使所经过的路程最短?
采用动态规划法
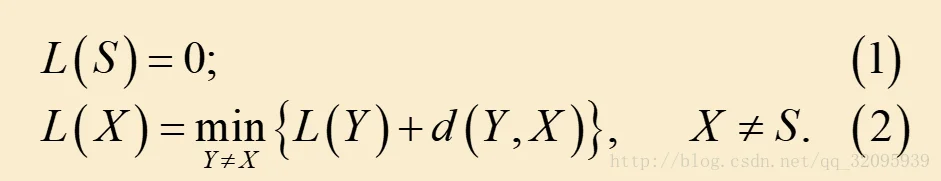
代码如下:
model:
sets:
CITIES/S,A1,A2,A3,B1,B2,C1,C2,T/:L;
ROADS(CITIES,CITIES)/
S,A1 S,A2 S,A3
A1,B1 A1,B2 A2,B1 A2,B2 A3,B1 A3,B2
B1,C1 B1,C2 B2,C1 B2,C2
C1,T C2,T/:D;
ENDSETS
DATA:
D= 6 3 3
6 5 8 6 7 4
6 7 8 9
5 6;
L=0, , , , , , , , ;
ENDDATA
@FOR(CITIES(i)|i#GT#@index(S):
L(i)=@MIN(ROADS(j,i):L(j)+D(j,i)););
end程序分析:
- “ROADS”(道路):由CITIES导出的一个派生集合(请特别注意其用法),由于只有一部分城市之间有道路相连,所以不应该把它定义成稠密集合,将其元素通过枚举给出,这就是一个稀疏集合。
- 在数据段对L进行赋值,只有L(S)=0已知,后面的值为空(但位置必须留出来,即逗号“,”一个也不能少,否则会出错)。如果这个语句直接写成“L=0;”,语法上看也是对的,但其含义是L所有元素的取值全部为0,所以也会与题意不符。
- 从模型中还可以看出:这个LINGO程序可以没有目标函数,这在LINGO中,可以用来找可行解(解方程组和不等式组)。
- 在@for循环中的过滤条件里用了一个函数“@index”, 其作用是返回一个元素在集合中的索引值,这里@index(S)=1(即元素S在集合中的索引值为1),所以逻辑关系式“I#GT#@index(S)”可以可以直接等价地写成“I#GT#1” 。这里@index(S)实际上还是@index(CITIES,S)的简写,即返回S在集合CITIES中的索引值。
结果截图
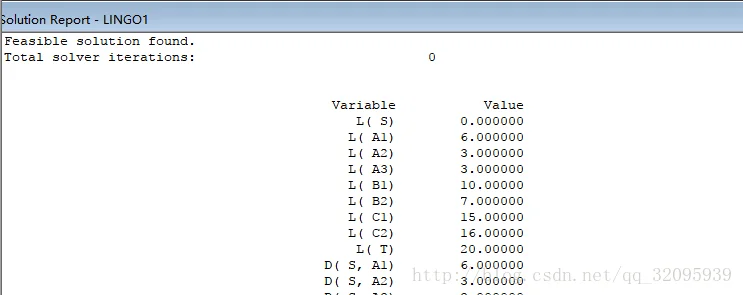
由此可得最优路径为S->S3->B2->C1->T。
一个匹配问题
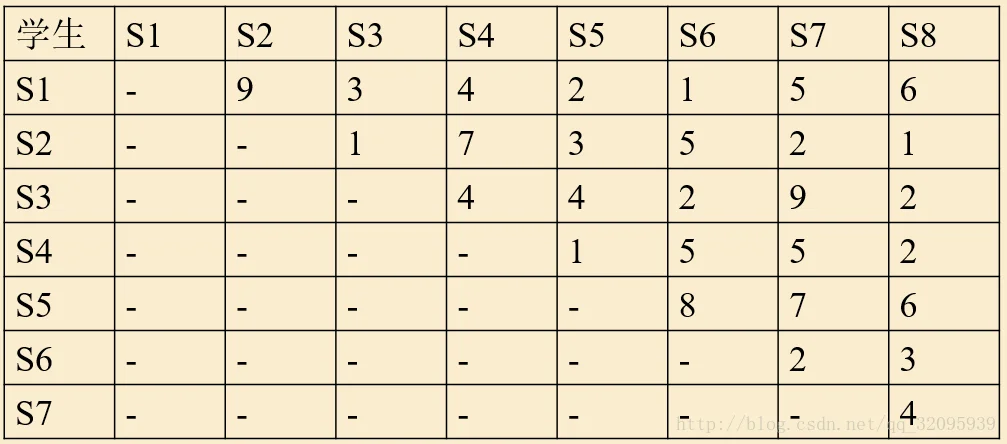
例 某班8名同学准备分成4个调查队(每队两人)前往4个地区进行社会调查。这8名同学两两之间组队的效率如下表所示(由于对称性,只列出了严格上三角部分),问如何组队可以使总效率最高?
问题分析:这是一个匹配(MATCHING)问题。把上表的效率矩阵记为BENEFIT(由于对称性,这个矩阵只有严格上三角部分共28个数取非零值)。用MATCH(Si,Sj)=1表示同学Si,Sj组成一队 ,而MATCH(Si,Sj)=0表示Si,Sj不组队。由于对称性,只需考虑i< j共28个0-1变量(而不是全部32个变量)。显然,目标函数正好是BENEFIT(Si,Sj)*MATCH(Si,Sj)对I,J之和。约束条件是每个同学只能(而且必须在)某一组,即对于任意i有:只要属性MATCH的某个下标为i就加起来,此和应该等于1。由上面的分析,因此,完整的数学模型如下(显然,这是一个0-1线性规划)。
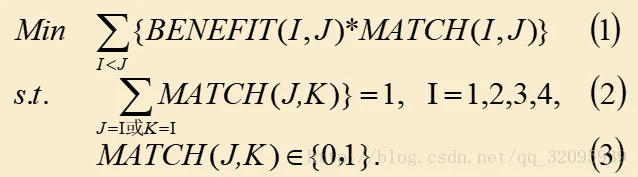
程序代码:
MODEL:
SETS:
STUDENTS/S1..S8/;
PAIRS(STUDENTS,STUDENTS)|&2#GT#&1:
BENEFIT,MATCH;
ENDSETS
DATA:
BENEFIT=
9 3 4 2 1 5 6
1 7 3 5 2 1
4 4 2 9 2
1 5 5 2
8 7 6
2 3
4;
ENDDATA
[OBJECTIVE] MAX=@SUM(PAIRS(I,J):BENEFIT(I,J)*MATCH(I,J));
@FOR(STUDENTS(I):[CONSTRAINTS] @SUM(PAIRS(J,K)|J#EQ#I#OR#K#EQ#I:MATCH(J,K))=1);
@FOR(PAIRS(I,J):@BIN(MATCH(I,J)));
END运行结果:
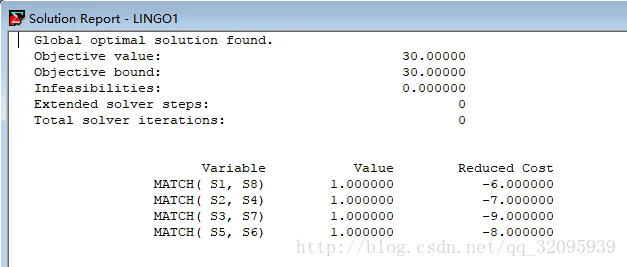
点击LINGO->SOLUTION
点击OK后,
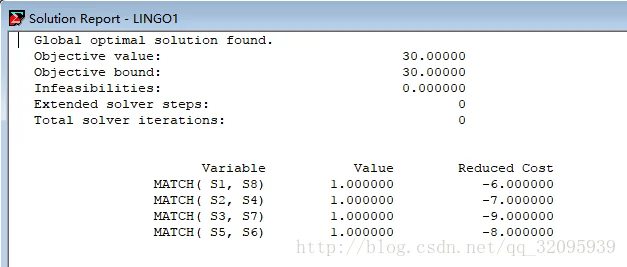
结果显示。
