Golang语言实现 实现二分查找,二分左侧查找,二分右侧查找,直接贴代码,涵盖详细注释,助力彻底搞明白,不在懵逼,解决一看就懂,一写就废。
package algorithmProject
import (
"fmt"
"testing"
)
func TestBinarySearch(t *testing.T) {
///下标:0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,16,17,18,19,20,21
arr := []int{0,1,2,3,4,4,4,5,6,7,8,9,9,9,10,12,23,43,54,67,89}
fmt.Println("BinarySearch res: ",BinarySearch(arr, 9))
fmt.Printf("\n")
fmt.Println("BinarySearchLeftBound res: ",BinarySearchLeftBound(arr, 9))
fmt.Printf("\n")
fmt.Println("BinarySearchRightBound res: ",BinarySearchRightBound(arr, 9))
}
//普通二分查找
func BinarySearch(arr []int,lookingfor int) int {
fmt.Printf("arr height %v,lookingfor:%v \n",len(arr),lookingfor)
var low=0
var height = len(arr)-1
//为什么是<=是因为上述 len -1 的原因
for low <= height {
/*
计算Mid的思路
如果直接用height /2 无法进行后续的计算
故需要low来临时标记拆分之后的数据的长度,根据下述判断条件,判断是降低还是提升高度
*/
var mid= low + (height-low) /2
var midValue=arr[mid]
fmt.Printf("low:%v ; height:%v ; mid :%v \n ",low,height,mid)
if midValue==lookingfor {//当找到目标时则停止寻找
return mid
}else if midValue < lookingfor{
//如果大于则在中位数拆分后的右边,故要用mid+1提升高度
low = mid + 1
}else if midValue > lookingfor{
//如果小于则在中位数拆分后的左边,故要用mid-1降低高度
height= mid - 1
}
}
fmt.Printf("end low:%v,height:%v \n",low,height)
return -1
}
//寻找左侧边界的二分查找
func BinarySearchLeftBound(arr []int,lookingfor int) int {
fmt.Printf("arr height %v,lookingfor:%v \n",len(arr),lookingfor)
var low=0
var height = len(arr)-1
for low <= height {
/*
计算Mid的思路
如果直接用height /2 无法进行后续的计算
故需要low来临时标记拆分之后的数据的长度,根据下述判断条件,判断是降低还是提升高度
*/
var mid=low + (height-low) /2
var midValue=arr[mid]
fmt.Printf("low:%v ; height:%v ; mid :%v ;midValue:%v \n ",low,height,mid,midValue)
/*
目标是查找左侧边界的数值,也就是每次拆分之后的左边数组
假设:拆分之后的左边数组 【9,9,10,12】
当等于或者查找的值大于目标值时,都需要降低高度 height = mid -1
再次拆分之后,查找的值小于目标值是则说明数据在右侧,则进要提升左侧的高度 也就是low = mid +1
最后low则是要找最左侧的值
*/
if midValue==lookingfor{
height = mid -1
}else if midValue < lookingfor{
low = mid + 1
}else if midValue > lookingfor{
height = mid -1
}
}
//防止越界情况
if low >= len(arr) || arr[low] != lookingfor {
return -1
}
fmt.Printf("end low:%v,height:%v \n",low,height)
return low
}
//寻找右侧边界的二分查找
func BinarySearchRightBound(arr []int,lookingfor int) int {
fmt.Printf("arr height %v,lookingfor:%v \n",len(arr),lookingfor)
var low=0
var height = len(arr)-1
//为什么是<=是因为上述 len -1 的原因
for low <= height {
/*
计算Mid的思路
如果直接用height /2 无法进行后续的计算
故需要low来临时标记拆分之后的数据的长度,根据下述判断条件,判断是降低还是提升高度
*/
var mid=low + (height-low) /2
var midValue=arr[mid]
fmt.Printf("low:%v ; height:%v ; mid :%v ;midValue:%v \n ",low,height,mid,midValue)
/*
目标是查找右层侧边界的数值,也就是每次拆分之后的右边数组
假设:拆分之后的右边数组 【8,9,9,9,10,12】
当等于或者查找的值小于目标值时,都需要提升右侧的高度 low = mid + 1
再次拆分之后,查找的值小于目标值是则说明数据在左侧,则要降低高低 也就是 height = mid -1
最后height 则是要找最右侧的值
*/
if midValue==lookingfor{
low = mid + 1
}else if midValue < lookingfor{
low = mid + 1
}else if midValue > lookingfor{
height= mid - 1
}
}
//防止越界情况
if height < 0 || arr[height]!= lookingfor{
return -1
}
fmt.Printf("end low:%v,height:%v \n",low,height)
return height
}
/*
总结:
只要二分查找则需要通过:low 临时变量记录下次拆分之后的len
var mid=low + (height-low) /2
普通二分查找:
判断等于则返回、小于则提升low高度、大于则降低height高度
说明:二分左侧、右侧查找,等于不直接返回是因不确认是否是最左或右侧
二分左侧查找:
等于或大于则降低height高度、小于则提升low的高度
二分右侧查找:
等于或小于则提升low高度、大于则降低height的高度
*/验证
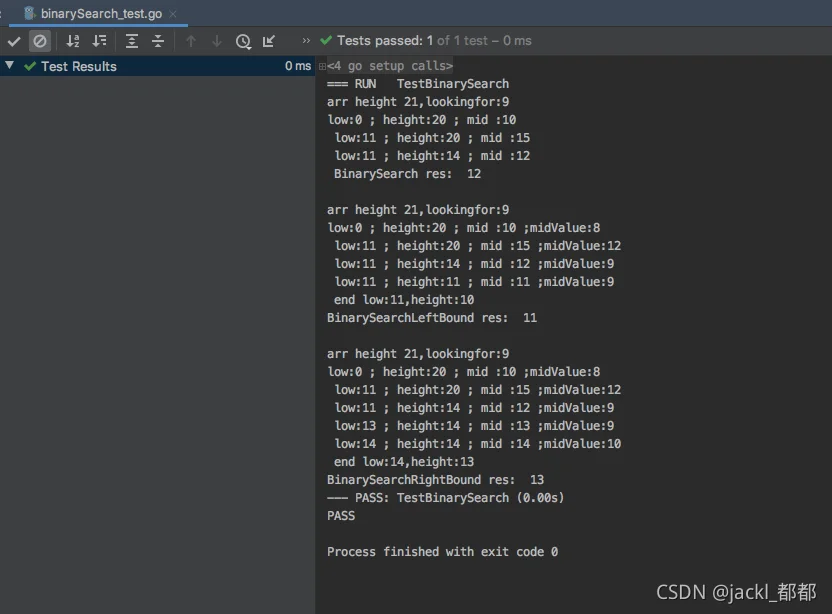
时间复杂度 O(log2n)
分析: 因为二分查找每次排除掉一半的不适合值,所以对于n个元素的情况:
一次二分剩下:n/2
两次二分剩下:n/2/2 = n/4
.....
m次二分剩下:n/(2^m)
在最坏情况下是在排除到只剩下最后一个值之后得到结果,即
n/(2^m)=1
所以由上式可得 : 2^m=n
进而可求出时间复杂度为: log2(n)
总结
所有二分查找共同原则:
需要通过:low 临时变量记录下次拆分之后的len
var mid=low + (height-low) /2
普通二分查找:
判断等于则返回、小于则提升low高度、大于则降低height高度
说明:二分左侧、右侧查找,等于不直接返回是因不确认是否是最左或右侧
二分左侧查找:
等于或大于则降低height高度、小于则提升low的高度
二分右侧查找:
等于或小于则提升low高度、大于则降低height的高度
