64dd165aa2370edaf7df21ec115cb784.png

今天是 Kevin 的算法之路的第6天。为大家讲解 LeetCode 热门题中的第 461 题，是一道经典的位运算的题，值得了解一波。

每日一笑

小学有一次写作文，要求展现出真实情感来。我后来就编了个妈妈冒雨去给菜地浇水的故事，将自己都感动得快哭了。结果，作文却不及格。老师给的评语是：“不尊重事实。”后来才发现，下大雨哪里还需要浇水啊。

题目描述

解题思路

两个数字对应二进制位不同的位置的数目。我们应该想到异或（XOR）位运算，当且仅当输入位不同时输出为1。

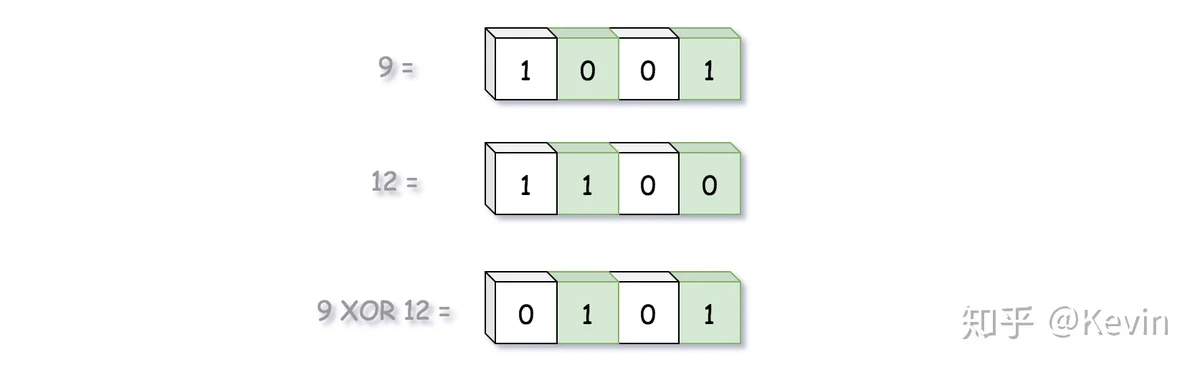
175fd513056ed5ea3ea9559d597df283.png 
xyx XOR y

现在问题就转化成了位计数问题。我们想想如何统计二进制数中1的位数呢？

方法一：内置函数

大多数编程语言中，都存在各种内置计算等于 1 的位数函数。比如 Java 中的 Integer.bitCount() ，Golang 中的 bits.OnesCount()

// java
class Solution {
    public int hammingDistance(int x, int y) {
        return Integer.bitCount(x ^ y); 
    }
}

//go
func hammingDistance(x int, y int) int {
 xor := x ^ y
 return bits.OnesCount(uint(xor))
}

方法二：移位

第一种方法虽然简单易写，在项目中写没有问题。但是如果在面试中，面试官可能就是要考查我们位计数，所以我们可以用移位操作来实现。

11

更准确的说，应该进行逻辑移位，移入零替换丢弃的位。

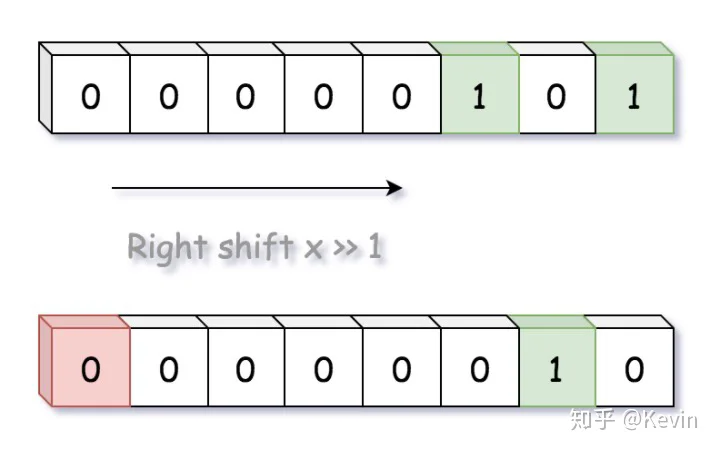
e69b22fe3db2f4fa7dd74c600f49e6a2.png 
i % 2i & 1
// java
class Solution {
  public int hammingDistance(int x, int y) {
    int xor = x ^ y;
    int distance = 0;
    while (xor != 0) {
      if (xor & 1 == 1)
        distance += 1;
      xor = xor >> 1;
    }
    return distance;
  }
}

//go
func hammingDistance(x int, y int) int {
 xor := x ^ y
 dis := 0
 for xor != 0 {
  if xor & 1 == 1 {
   dis += 1
  }
  xor = xor >> 1
 }
 return dis
}

方法三：布赖恩·克尼根算法

这个方法来自官方题解，感觉有点牛逼，分享一下。

思路

方法二是逐位移动，逐位比较边缘位置是否为 1。寻找一种更快的方法找出等于 1 的位数。

是否可以像人类直观的计数比特为 1 的位数，跳过两个 1 之间的 0。例如：10001000。

上面例子中，遇到最右边的 1 后，如果可以跳过中间的 0，直接跳到下一个 1，效率会高很多。

这是布赖恩·克尼根位计数算法的基本思想。该算法使用特定比特位和算术运算移除等于 1 的最右比特位。

当我们在 number 和 number-1 上做 AND 位运算时，原数字 number 的最右边等于 1 的比特会被移除。
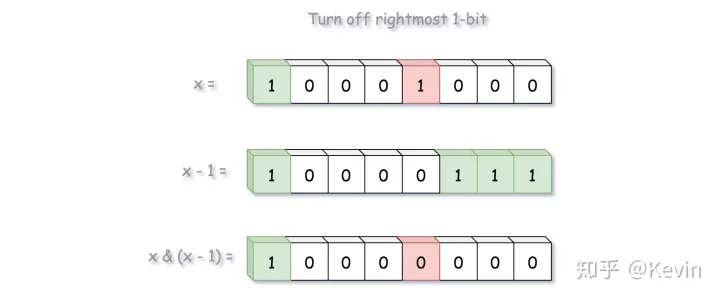
db7b998ee0dea01b86788ad2c864345e.png 
10001000
//java
class Solution {
  public int hammingDistance(int x, int y) {
    int xor = x ^ y;
    int distance = 0;
    while (xor != 0) {
      distance += 1;
      // remove the rightmost bit of '1'
      xor = xor & (xor - 1);
    }
    return distance;
  }
}

//go
func hammingDistance(x int, y int) int {
 xor := x ^ y
 dis := 0
 for xor != 0 {
  dis += 1
  xor = xor & (xor - 1)
 }
 return dis
}
郑重声明：
所展示代码已通过 LeetCode 运行通过，请放心食用～

在唠唠嗑 

216.65216.610066.6