最近在复习算法的时候 发现之前的一些基础的算法都忘记了。就在这里总结一下和大家分享,并附上golang的代码实现。
1.冒泡排序算法
名字的由来:这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名“冒泡排序”。
方法的原理:冒泡排序算法清楚地演示了排序是如何工作的,同时又简单易懂。冒泡排序步骤遍历列表并比较相邻的元素对。如果元素顺序错误,则交换它们。重复遍历列表未排序部分的元素,直到完成列表排序。
简单点来讲冒泡排序算法主要思想就是每一次确定一个值。如果是从左开始比较就是通过两两比较找到最大值。如果是从右开始比较就是两两比较找到最小值。 如下图所示
时间复杂度:因为冒泡排序重复地通过列表的未排序部分,所以它具有最坏的情况复杂度O(n^2)。
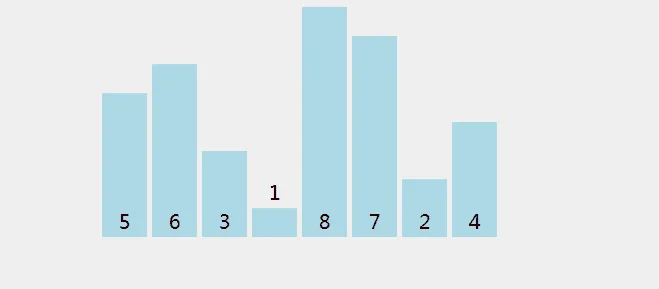
上图描述的就是从左开始比较 两两比较确定最大值的例子。
//用golang实现冒泡排序
package main
import "fmt"
func main() {
values := []int{5,6,3,1,8,7,2,4}
fmt.Println(values)
BubbleAsort(values)
BubbleZsort(values)
}
func BubbleAsort(values []int) {
for i := 0; i < len(values)-1; i++ {
for j := i+1; j < len(values); j++ {
if values[i]>values[j]{
values[i],values[j] = values[j],values[i]
}
}
}
fmt.Println(values)
}
func BubbleZsort(values []int) {
for i := 0; i < len(values)-1; i++ {
for j := i+1; j < len(values); j++ {
if values[i]<values[j]{
values[i],values[j] = values[j],values[i]
}
}
}
fmt.Println(values)
}
2.选择排序算法
算法思想:线性搜索数列并找到最小值。将最小值替换为数列中最左端的数字并进行排序。如果最小值已经在最左端则不进行操作。重复此操作直到数列排序完成。
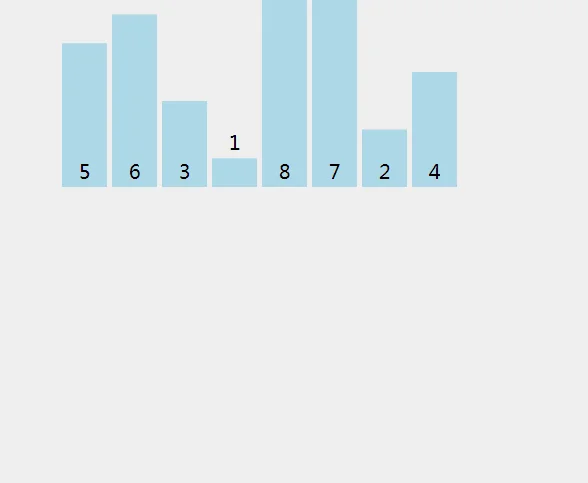
简单来说就是每次找到数列的最小值并和最左端还没确定的值进行替换。也可以找最大值和最右端没确定的值替换。 如下图所示
时间复杂度:最坏时间复杂度:O(n^2)。

上图描述的就是按照找最小值来确定位置的例子。
//golang 实现选择排序算法
package main
import "fmt"
func main() {
numbers := []int{6, 2, 7, 5, 8, 9}
SelectSort(numbers)
fmt.Println(numbers)
}
func SelectSort(values []int) {
length := len(values)
if length <= 1 {
return
}
for i := 0; i < length; i++ {
min := i // 初始的最小值位置从0开始,依次向右
// 从i右侧的所有元素中找出当前最小值所在的下标
for j := length - 1; j > i; j-- {
if values[j] < values[min] {
min = j
}
}
//fmt.Printf("i:%d min:%d\n", i, min)
// 把每次找出来的最小值与之前的最小值做交换
values[i], values[min] = values[min], values[i]
//fmt.Println(values)
}
}
3.插入排序算法
算法思想:左端的数字已经完成排序。取出那些尚未操作的最左端的数字将这个数字与已经完成排序的数字进行比较如果左边的数字较大则交换两个数字的位置。重复此操作直到出现一个比当前较小的数字或者数字已经到达最左端。 如下图所示
时间复杂度:最坏情况下时间复杂度为O(n^2)。最好情况下为O(n)
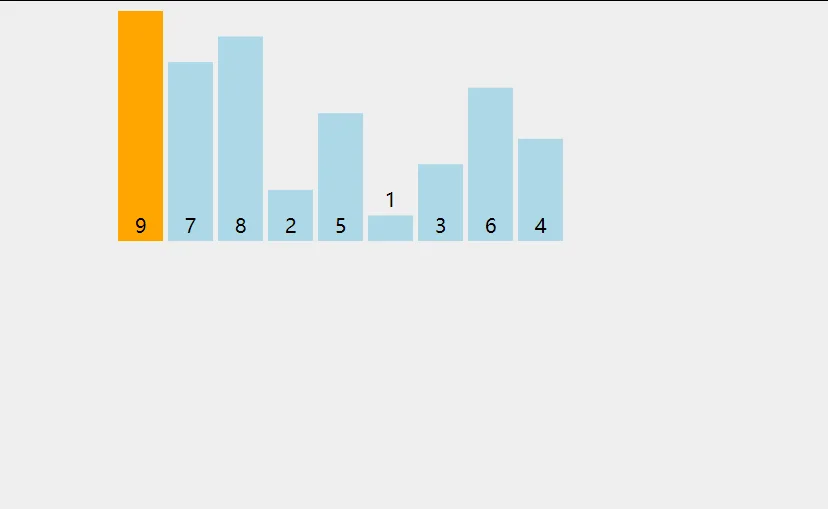
上图描述的就是插入排序算法的例子。
// golang 实现插入排序
package main
import "fmt"
func main() {
numbers := []int{6, 2, 7, 3, 8, 5}
InsertSort(numbers)
fmt.Println(numbers)
}
func InsertSort(values []int) {
length := len(values)
if length <= 1 {
return
}
for i := 1; i < length; i++ {
tmp := values[i] // 从第二个数开始,从左向右依次取数
key := i - 1 // 下标从0开始,依次从左向右
// 每次取到的数都跟左侧的数做比较,如果左侧的数比取的数大,就将左侧的数右移一位,直至左侧没有数字比取的数大为止
for key >= 0 && tmp < values[key] {
values[key+1] = values[key]
key--
//fmt.Println(values)
}
// 将取到的数插入到不小于左侧数的位置
if key+1 != i {
values[key+1] = tmp
}
//fmt.Println(values)
}
}
4.快速排序算法
算法思想:快速排序算法与其他算法相比,它的特点是数字比较和交换的次数较少,在许多情况下可以高速地进行排序。
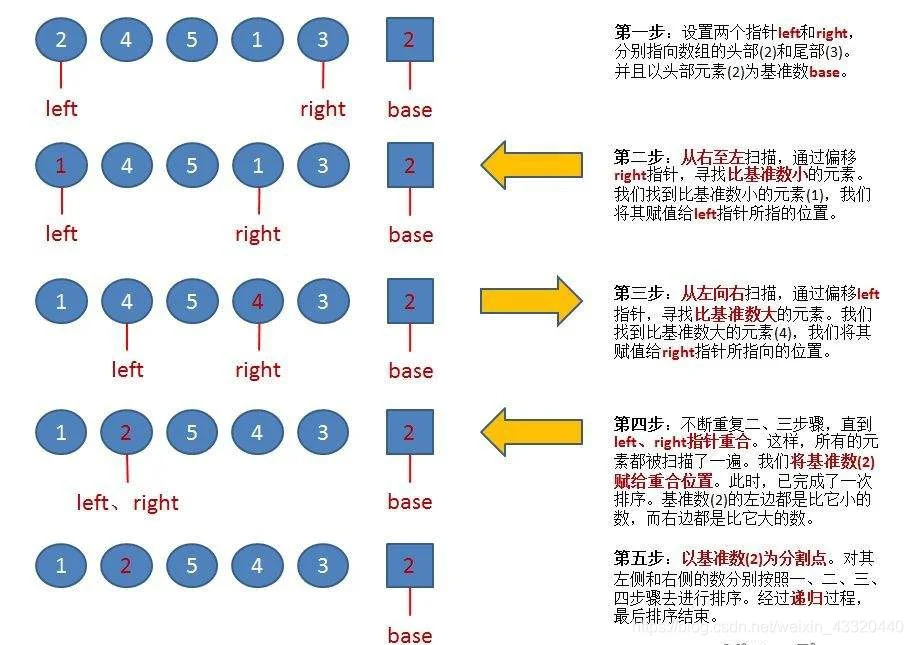
- 第一步:选择数列中的一个数字作为排序的基准,这个数字被称为pivot。pivot通常选择一个随机的数字,在这里我们默认选择最右边的数字作为pivot。我们把这个数字做个标记记为p。
- 第二步:在最左边的数字上标记为左标记,最右边的数字标记为右标记。快速排序是一种使用这些标记递归的重复一系列操作的算法。
- 第三步:我们将左边的标记像右移动,当左边的标记的数字超过了pivot的数字时,停止移动。之后将右标记向左移动,当右标记的数字小于pivot时停止移动。当左右侧的标记都停止时,交换这两个数字的位置。(左标记的作用是找到一个大于pivot的数字,右标记是找到小于pivot的数字,通过交换数字可以在数列的左侧收集小于pivot的数字,右侧收集大于pivot的数字)。交换之后重复第二步操作。( 情况1:当左标记找到比pivot大的数字 停止移动,右标记开始移动并且碰到了左标记所在的位置。则将当前位置的数字和pivot位置进行交换。情况2:当左标记移动和右标记碰撞时并不会停止移动,当左标记达到数列最右边时停止移动,这意味着pivot数字在这个数列里是最大值)
- 第四步:因为pivot已经找到了数列中的位置,则对pivot左侧和右侧的数列 分成两部分并递归的执行前三步的步骤。(当操作的数列只有一个数字 则认为已经完成了排序)
时间复杂度:最坏情况为O(n^2) 最好情况O(nlog(n)) 平均情况为O(nlogn)
package main
import "fmt"
/*
快读排序
快排的思想 就是定一个目标值 确定这个目标值的位置 之后在对目标值两侧的数组
递归的进行上述操作
时间复杂度是最快和平均O(nlogn) 最慢 O(n^2)
*/
func quickSort(array []int, start, end int) {
if start < end {
left := start
right := end
pivot := array[start]
for left < right {
for left < right && array[right] >= pivot {
right--
}
if left < right {
array[left] = array[right]
left++
}
for left < right && array[left] <= pivot {
left++
}
if left < right {
array[right] = array[left]
right--
}
}
array[left] = pivot
quickSort(array, start, left-1)
quickSort(array, left+1, end)
}
fmt.Println(array, "返回排序之后的array数组")
}
func main() {
arrayList := []int{5, 4, 7, 2, 8, 10, 8}
quickSortTest(arrayList, 0, len(arrayList)-1)
}
5.归并排序算法
算法思想:
- 第一步:将数字分成两半,重复此步骤直到每个数字成为一部分。
- 第二步:合并数字,合并时按照数字的升序移动,使得合并后的数字在组内按升序排列。递归的重复组的合并操作,直到所有数字都在一个组中。
时间复杂度:O(nlogn)
// golang实现归并排序
package main
import fmt "fmt"
func main () {
/*
生成需要排序的队列100~1
*/
length:=100
A:=make([]int,length)
j:=length
for i:=0;i<length;i++{
A[i]=j
j--
}
/*
排序
*/
MergeSort(A,0,length-1)
/*
输出排序后的队列
*/
for i:=0;i<length;i++{
fmt.Println(A[i])
}
}
/*
归并排序
*/
func MergeSort(Arrary []int,p int,r int) {
if p<r {
q:=0
if(r-q+1)%2==0{
q=(p+r-1)/2
}else{
q=(p+r)/2
}
MergeSort(Arrary,p,q)
MergeSort(Arrary,q+1,r)
Merge(Arrary,p,q,r)
}
}
/*
两列已排序的数组合并
*/
func Merge(Arrary []int,p int,q int,r int) {
n1:=q-p+1
n2:=r-q
L_Arr:=make([]int,(n1+1))
R_Arr:=make([]int,(n2+1))
for i:=0;i<n1;i++{
L_Arr[i]=Arrary[p+i]
}
L_Arr[n1]=1000;
for i:=0;i<n2;i++{
R_Arr[i]=Arrary[q+1+i]
}
R_Arr[n2]=1000;
iLnum:=0
iRnum:=0
for i:=p;i<r+1;i++{
if L_Arr[iLnum]<R_Arr[iRnum] {
Arrary[i]=L_Arr[iLnum]
iLnum++
}else{
Arrary[i]=R_Arr[iRnum]
iRnum++
}
}
}
ps:此博客图片都来源于网络
