
多年前就听过这个动态规划,最近在复习常用算法的时候才认真学习了一下,发现蛮有意思,和大家安利一波。
定义:
准确来说,动态规划师吧一个复杂问题分解成若干个子问题,并且寻找最优子问题的一种思想,而不是一种特定的算法。
听上去和我们常用的递归有点类似,但是注意:其中子问题的解被重复使用。也就是利用这个特性,我们可以把一个复杂的问题抽象转换成一个简单二维表来进行推演。
动态规划的解题关键在于:
- 1.根据问题可能性进行拆分。
从最简单的情况下进行分析,从下往上逐步分析。 - 2.找到状态转移方程式,保存最优解。
方程式其实就是在满足某个条件下的递推通项公式,同时也要注意条件范围和边界处理。
最有名的是背包问题:将N种类型的物件放到一个容量为M的背包里面,寻找最优解。
一般来说可以用暴力枚举的方式去算近似最优,但是从空间复杂度和时间复杂度来看使用动态规划更好,因为每一步的结果会保存下来给下一步计算使用,节约了不少时间消耗,最终算法性能极高。
下面举一个典型的例子,来自牛客网的一道"凑整题":
给你六种面额 1、5、10、20、50、100 元的纸币,假设每种币值的数量都足够多,编写程序求组成N元(N为0~10000的非负整数)的不同组合的个数。
仔细分析后发现,这是一个用不同类型的面额组合拼凑固定金额的组合最优解问题。由于N为0 ~ 10000的非负数,我们可以假设N取10来分析。
分析结果如图:
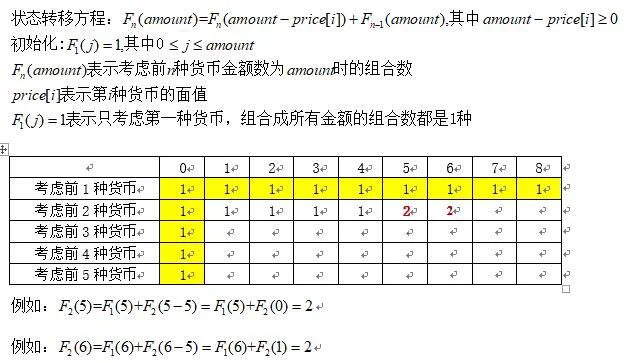
伪代码如下:
if (j - price[i] >= 0) {
Fn(amount) = Fn(j - price[i]) + Fn-1(amount);
} else {
Fn(amount) = Fn-1(amount);
}
其中的Fn函数可以用一个二维数组来实现,第二维为面额个数(即n),第一维度为amount+1种,用于对应的组合数。
用golang实现如下:
func getTheNum(num int) int {
var dp [5][10000]int
moneys = int[...] {1, 5, 10 ,20 , 50, 100}// 面额数组
for i := 0; i < 5; i++ { // 用前i种面额拼凑1rmb的方法数均为1
dp[i][0] = 1
}
for i := 0; i <= num; i++ { // 用1rmb面额拼凑0金额的方法数都为1
dp[0][i] = 1
}
for i := 1; i < 5; i++ { // 每一种面额组合递推
for j := 1; j <= num; j++ {
if j - moneys >= 0 { // 当当前金额大于这次循环的面额值,则组合数等于当前i种面额拼凑j金额的组合数+前i+1种面额拼凑j - moneys[i]金额的组合数
dp[i][j] = dp[i-1][j] + dp[i][j - moneys[i]]
} else {
dp[i][j] = dp[i-1][j]
}
}
}
return dp[4][num] // 返回最后一项
}
还可以进一步简化,因为二维数组保存的结果在每一次循环判断中都被保存下来了,所以用一维数组也可以保留。改进实现如下:
func SimpleGetNum(num int) int {
var dp [10000]int
moneys = int[...] {1, 5, 10 ,20 , 50, 100}// 面额数组
for i := 0; i <= num; i++ { // 用1rmb面额拼凑0金额的方法数都为1
dp[i] = 1
}
for j := 1; j <= 5; j++ {
for i := 1; i <= num; i++ {
if i >= moneys[j] { // 当前面金额大于面额的时候需要计算前i种面额组合出i - moneys[j]的方法数
dp[i] += dp[i - moneys[j]]
}
}
}
return dp[num]
}
探索的过程就如同RPG游戏,算法真的是一个很有趣的事情,很多都像精巧的数学问题的代码化。

