
树一种非常重要的数据结构:由n个有限节点组成的具有层次关系集合;
很多人学习树的时候,觉得挺难,内容又多,操作又复杂,主要原因我认识一是对树的一些术语不够熟练,二是没有沉下心来研究透树的基础;
虽然树的衍生形式很多,但是树的基础就那几种,其余的都是在树的基础之上推演出来的;
往深了说,数组和链表、栈和队列、树三者又何尝不是层层递进的关系呢,理论上你对数组和链表掌握足够了,你学起来栈和队列就不是问题,你对栈和队列熟悉之后,研究二叉树的时候自然不是问题;二叉查找树又是一种特定规则的二叉树,AVL树和红黑树等又是基于二叉查找树的优化;
因此,你看当你掌握了一些基础的核心知识点之后,其余的衍生出来的内容都不在话下,再学习他们只不过是为了让我们在思考问题和使用的时候,能够更加快速的从记忆中拉出来;
树的定义
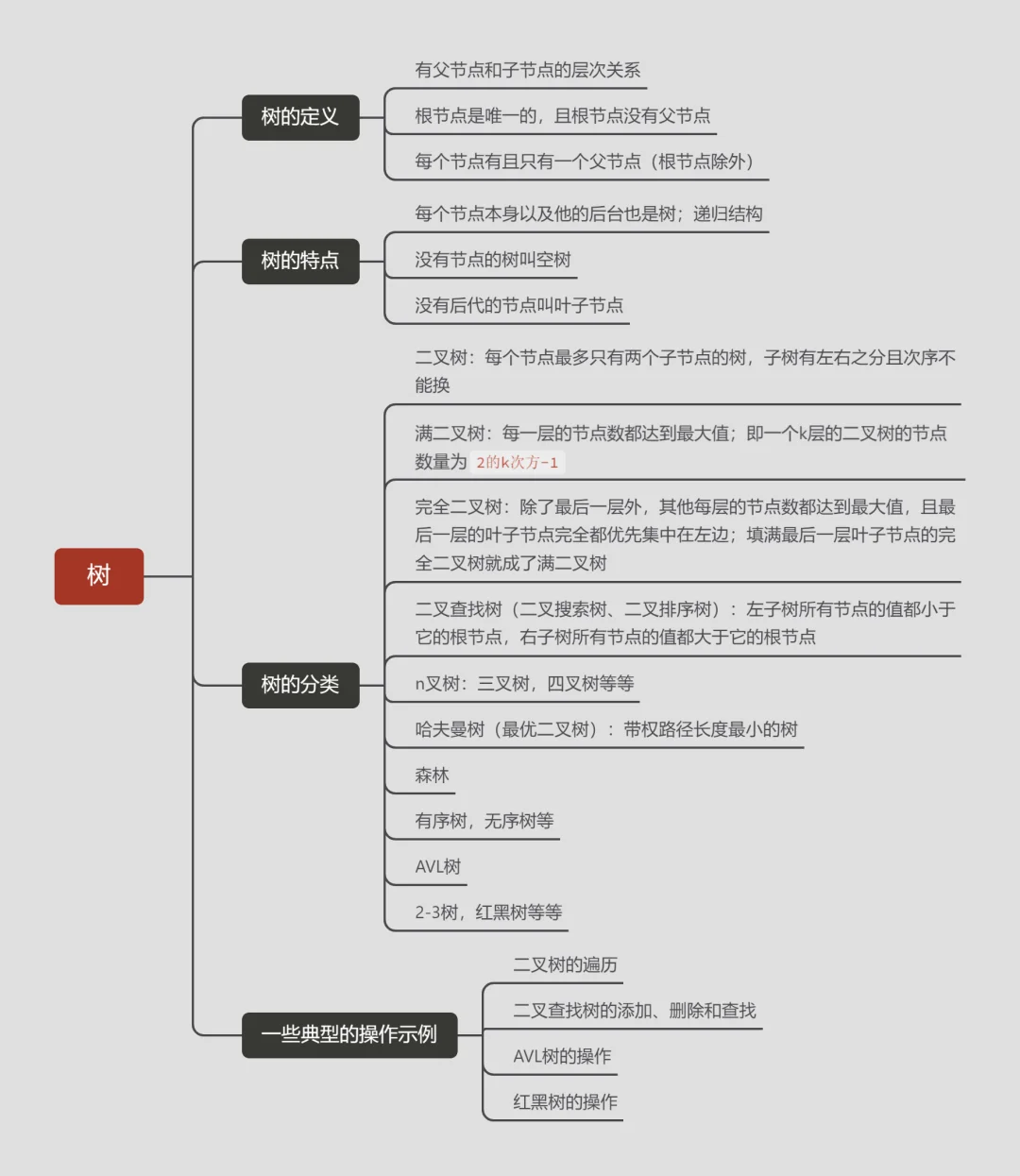
有节点间的层次关系,分为父节点和子节点。
有唯一一个根节点,该根节点没有父节点。
除了根节点,每个节点有且只有一个父节点。
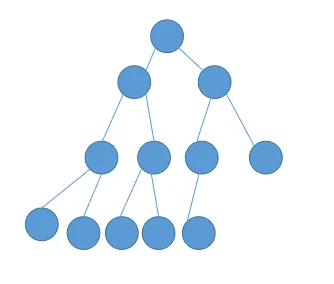
树的示意图:
关于树的一些术语
空树:没有节点的树称为空树
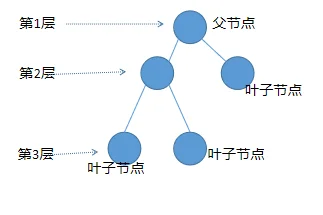
结点的度:结点拥有的子树的数目;如下图所示,节点4下有两个节点8和9,所以节点4的度为2
叶子:没有后代的节点称为叶子节点,即度为零的结点;如下图所示,节点8和9的度为0,因此89也叫叶子节点
树的度:树中结点的度最大的值就是这棵树的度;如下图所示,节点3的度为3,是最大的度值,因此整棵树的度为3
层次:根结点的层次为1,其余结点的层次等于该结点的双亲结点的层次加1;如下图所示,节点1是第一层,节点23是第二层,节点4567是第三层,节点89是第四层
树的高度:树中结点的层次的最大值就是树的高度;如下图所示,这棵树的层次为4
森林:0个或多个不相交的树组成,对森林加上一个根,森林即成为树,删去根,树即成为森林
二叉树的定义
每个节点最多有两个子树
关于二叉树有一些数学特性,这里不做讨论,感兴趣的可以自己搜索;
满二叉树的定义及示意图
2的k次方-1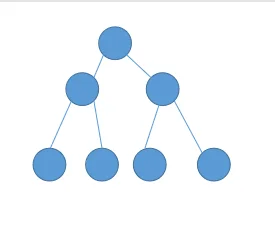
完全二叉树的定义及示意图:
二叉树定义的基础上,除了最后一层外,其他每层的节点数都达到最大值,且最后一层的叶子节点完全都优先集中在左边;
填满最后一层叶子节点的完全二叉树就成了满二叉树;
golang实现二叉树
基于链表来实现二叉树:
// 设计二叉树的结构体
// 利用单向表的特点和二叉树的相似之处来设计:
// 1.树是一种递归的形式,且在每个节点之间链接和存储
// 2.二叉树仅有左右子树
type TreeNode struct {
Data int // 用于存储数据
Left *TreeNode // 左子树
Right *TreeNode // 右子树
}
如果想用数组来设计二叉树,倒也不是不可以,但是一般用来表示完全二叉树,且基于数学运算来定位父节点和子节点的关系:
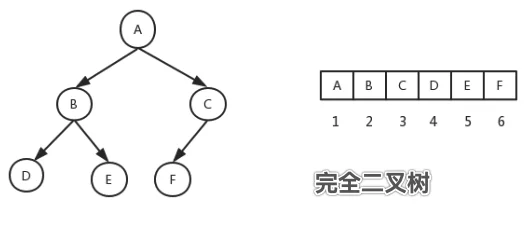
从上到下,从左到右1表示树根节点
编号为i的节点的左右节点分别是:2i,2i+1
编号为i的节点的父节点是:i/2取整
下篇分享
以上是关于树的一些概念理解,后面我们将会用golang来实现一些示例:
golang实现二叉树的遍历
golang实现二叉查找树的操作
golang实现AVL树的操作
golang实现红黑树的操作
关注李二狗 持续精进
坚持每日输出go开发+面试题+算法+工作经验等后端相关技术
关于我今年的计划请查看:
更多博客内容请查看原文链接
