Golang官方一致性哈希组件详解

背景

在分布式缓存中，我们需要通过一组缓存节点来提高我们的缓存容量。比如我们有3个Redis节点：

最简单的路由规则是我们计算`Key`的哈希值，然后取模计算目标节点，比如我们有5个Key，计算出以下哈希值及对应的目标节点：

Key的哈希值	模3的余	目标节点
10	1	Redis1
4	1	Redis1
6	0	Redis0
8	2	Redis2
15	0	Redis0

如果我们这时候加入一个新的Redis节点，这时候路由变化如下：

Key的哈希值	模3的余	目标节点（旧）	模4的余	目标节点（新）	是否变化
10	1	Redis1	2	Redis2	是
4	1	Redis1	0	Redis0	是
6	0	Redis0	2	Redis2	是
8	2	Redis2	0	Redis0	是
15	0	Redis0	3	Redis3	是

缓存雪崩

为了解决这个问题，一般我们会使用一致性哈希：

一致性哈希算法

一致性哈希算法经常被用于请求路由中，在处理节点不变的情况下，它能够把相同的请求路由到相同的处理节点上。同时还能在处理节点变动时，让相同请求尽可能的打到原先相同的处理节点上。

原理

2^32

图中有三个Redis节点，通过哈希映射到环上的某个位置。Key也是通过哈希映射到环上的某个位置，然后向前寻找计算节点，第一个遇到的就是Key的目标节点。

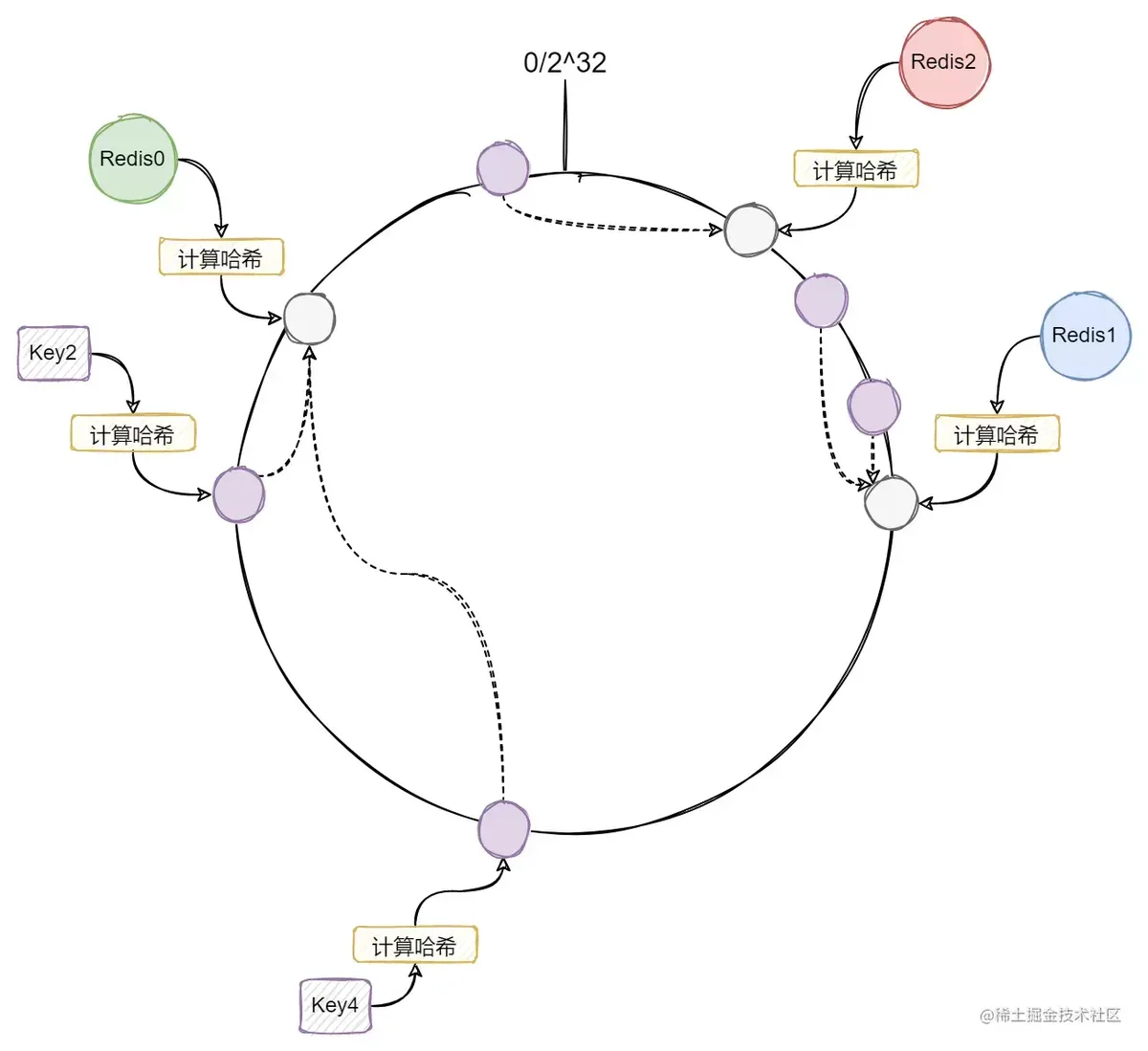
这时候如果我们加入一个新的Redis3节点，可以看到只有Key4的路由改变了，其他的Key的路由都保持不变：

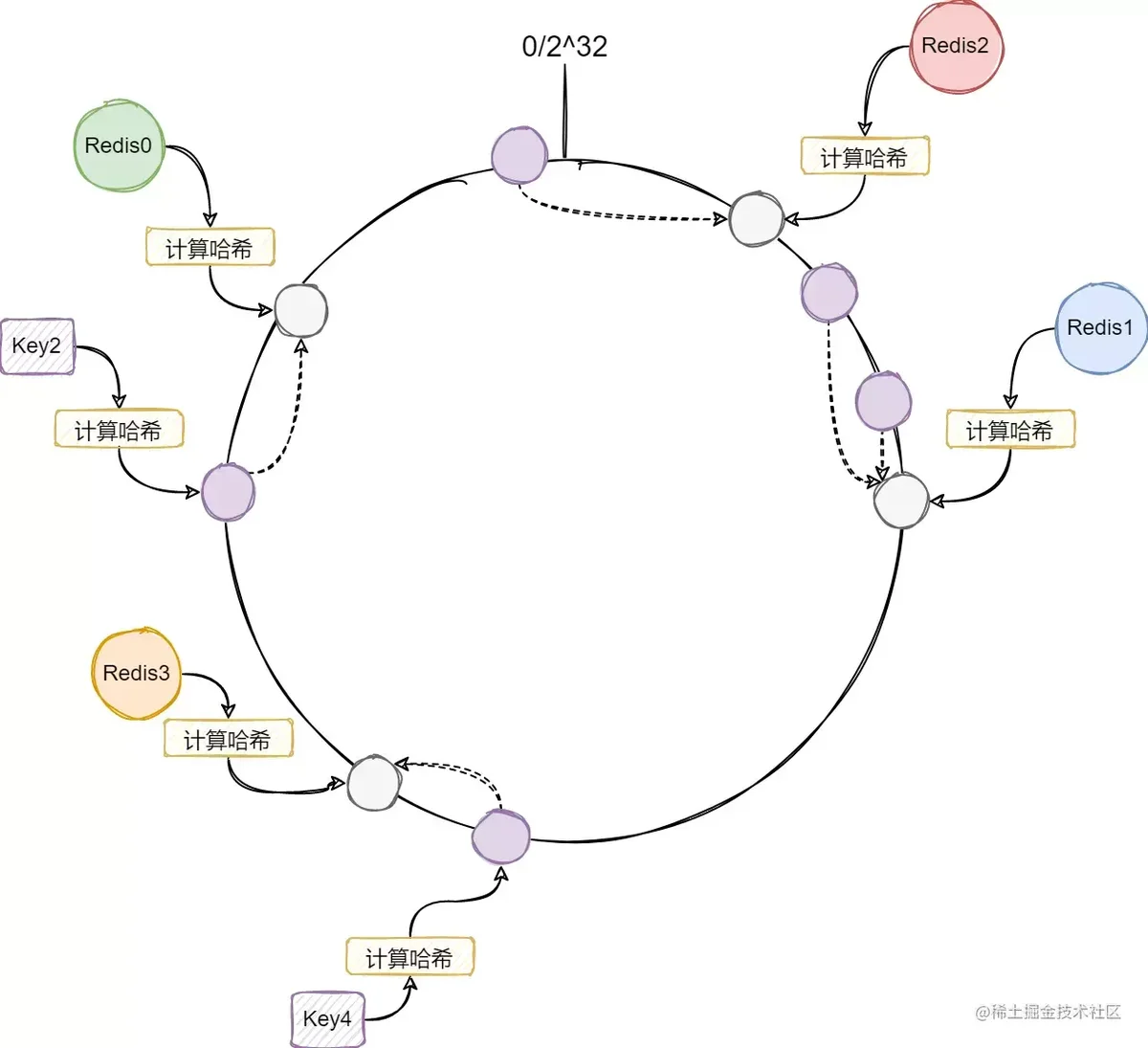也就是我们新加入的处理节点，只会影响前面的处理节点的路由。

改进

可以看到上面的Redis节点在环上分布得并不均匀，这样会导致每个节点的负载差距过大。为了让Redis节点在环上分布得更加均匀，我们还可以再加入虚拟节点。让一个Redis节点能够映射到哈希环上的多个位置，这样节点的分布会更加均匀。

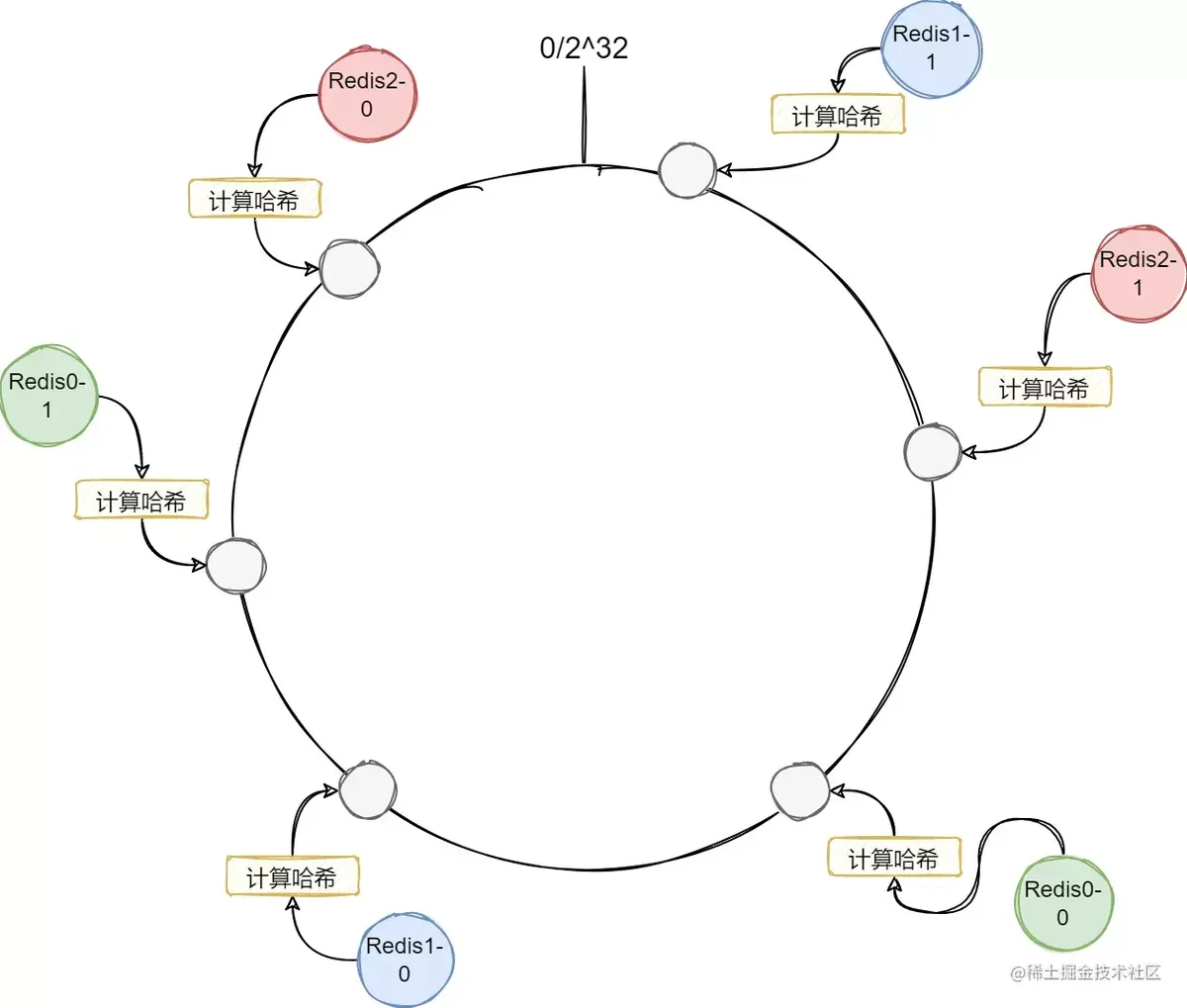
可以看到因为每个Redis节点的映射位置变多了，因此更有可能会分布得更加均匀。图里每个Redis节点只有两个虚拟节点，主要是不太好画，实际上我们可能会给每个Redis节点分配几十个虚拟节点，这样基本上就很均匀了。

实现方式

groupcache

下面的代码对这个实现有一些修改。

结构和接口

crc32

ring数组nodesring数组

// 哈希函数
type Hash func(data []byte) uint32

// 哈希环
// 注意，非线程安全，业务需要自行加锁
type HashRing struct {
	hash Hash
	// 每个真实节点的虚拟节点数量
	replicas int
	// 哈希环，按照节点哈希值排序
	ring []int
	// 节点哈希值到真实节点字符串，哈希映射的逆过程
	nodes map[int]string
}

添加节点

可以看到这个方法是把节点添加到哈希环里面，这里会为每个节点创建虚拟节点，这样可以分布的更加均匀。

当然这个方法存在一个问题，就是它没有判断加入的节点是否已经存在，这样可能会导致Ring上面存在相同的节点。

// 添加新节点到哈希环
// 注意，如果加入的节点已经存在，会导致哈希环上面重复，如果不确定是否存在请使用Reset
func (m *HashRing) Add(nodes ...string) {
	for _, node := range nodes {
		// 每个节点创建多个虚拟节点
		for i := 0; i < m.replicas; i++ {
			// 每个虚拟节点计算哈希值
			hash := int(m.hash([]byte(strconv.Itoa(i) + node)))
			// 加入哈希环
			m.ring = append(m.ring, hash)
			// 哈希值到真实节点字符串映射
			m.nodes[hash] = node
		}
	}
	// 哈希环排序
	sort.Ints(m.ring)
}

重置节点

为了解决上面的问题，我们额外实现了一个重置方法，也就是先清空哈希环，再添加。当然这样就必须每次都指定完整的节点列表。

// 先清空哈希环再设置
func (r *HashRing) Reset(nodes ...string) {
	// 先清空
	r.ring = nil
	r.nodes = map[int]string{}
	// 再重置
	r.Add(nodes...)
}

获取Key对应的节点

这个方法的功能是查询Key应该路由到哪个节点，也就是计算Key的哈希值，然后找到哈希值对应的处理节点（这里需要考虑ring数组逻辑上是一个环），然后再根据这个哈希值去寻找真实处理节点的字符串。

// 获取Key对应的节点
func (r *HashRing) Get(key string) string {
	// 如果哈希环位空，则直接返回
	if r.Empty() {
		return ""
	}

	// 计算Key哈希值
	hash := int(r.hash([]byte(key)))

	// 二分查找第一个大于等于Key哈希值的节点
	idx := sort.Search(len(r.ring), func(i int) bool { return r.ring[i] >= hash })

	// 这里是特殊情况，也就是数组没有大于等于Key哈希值的节点
	// 但是逻辑上这是一个环，因此第一个节点就是目标节点
	if idx == len(r.ring) {
		idx = 0
	}

	// 返回哈希值对应的真实节点字符串
	return r.nodes[r.ring[idx]]
}

总结

这个一致性哈希的实现非常简单，功能上也非常简单（官方的实现甚至没有Reset()方法），可以通过这个实现理解一致性哈希的原理。也可以直接在业务中使用它，如果功能不够再根据需求进行扩展。