2021.11.1
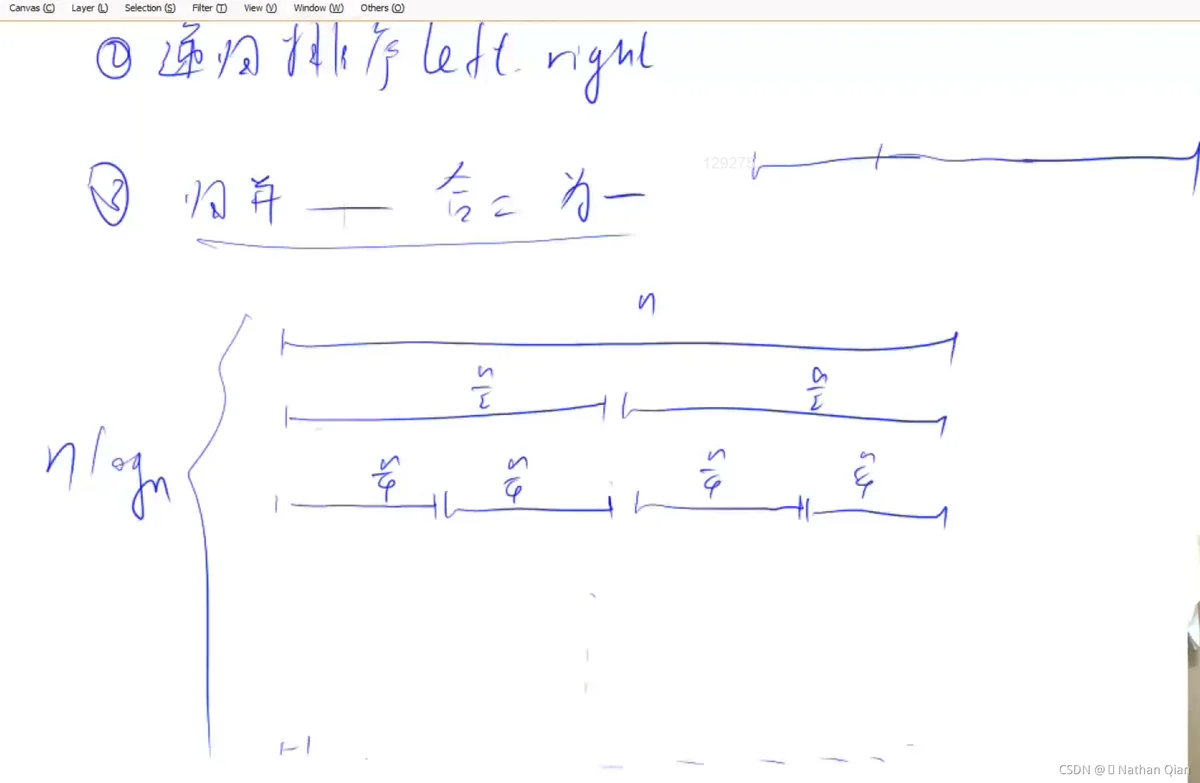
每一层都是n，分割n为n/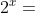
，直到等于1
所以x=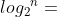
（层数）
所以时间复杂度为O（n)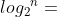
先进行递归排序，这样当区间长度为1的时候，逐渐放大区间，将每个区间的左办部分和右半部分都完成排序，最终回到一开始调用递归的区间。
1.[L,R]--->[L,mid],[mid+1,R]
2.递归排序[L,mid]和[mid+1,R]
3.归并，将左右两个有序序列合并成一个有序序列
归并排序（分治）稳定 o（nlogn(底数为2))logn为层数
1.确定分界点 mid=(l+r)/2;
2.递归排序left,right.
3.归并，合二为一
在一个数列中，如果相同的数排完序位置相同
则这个算法是稳定的
void merge_sort(int q[], int l, int r)
{
if (l >= r) return;
int mid = l + r >>1;
merge_sort(q, l, mid), merge_sort(q, mid + 1, r);
int k = 0, i = l,j = mid + 1;
while (i <= mid && j <= r)
{
if (q[i] <= q[j])tmp[k++] = q[i++];
else tmp[k++] = q[j++];
}
while (i <= mid)tmp[k++] = q[i++];
while (j <= r)tmp[k++] = q[j++];
for (i = l, j = 0; i <= r; i++, j++)q[i] = tmp[j];
}
int main()
{
cin>>n;
for (int i = 0; i < n; i++)cin>>a[i];
merge_sort(a, 0, n - 1);
for (int i = 0; i < n; i++)cout << a[i] <<" ";
return 0;
}
2021.11.3
i<j,a[i]>a[j],则a[i],a[j]为逆序对
假设可以在归并排序的同时返回所有逆序对的个数
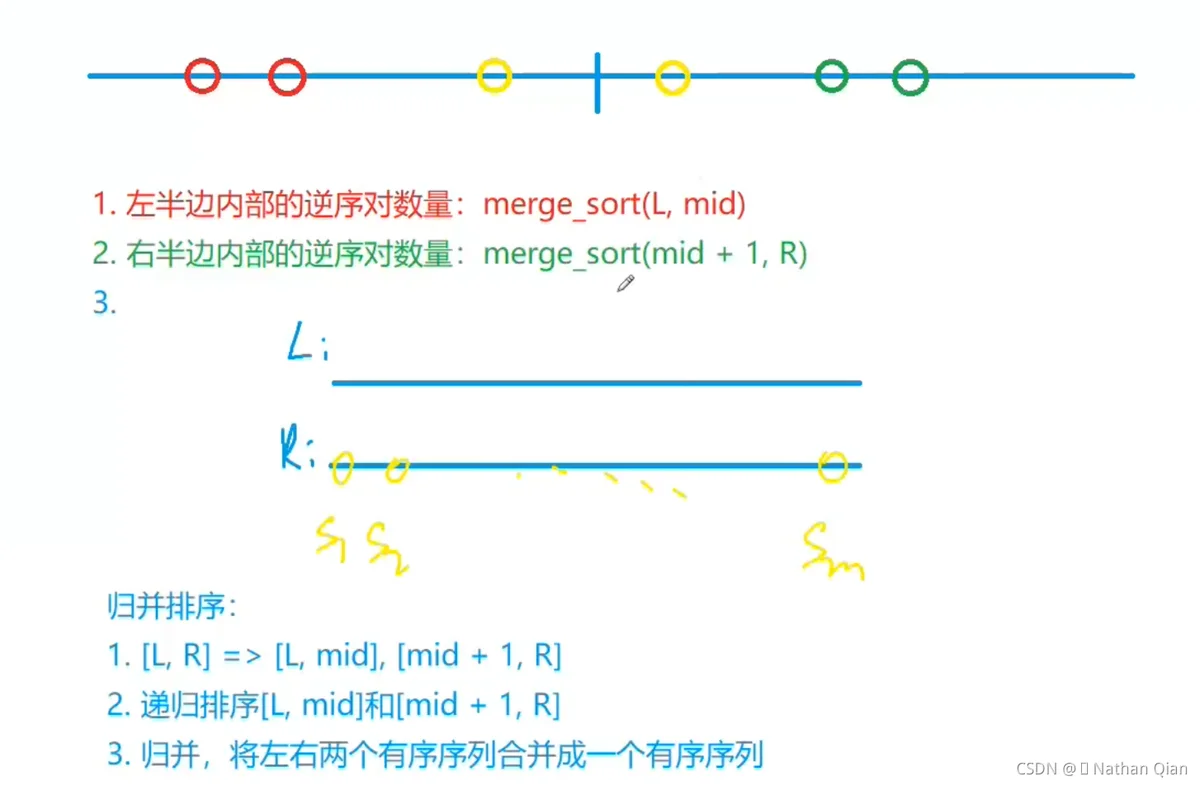
对于黄色逆数对的个数
用两个指针i,j；找到a[i]>a[j];a[i]后面的数必然严格大于a[j]
所以逆数对数量Sj=mid-i+1;
逆数对的最大个数：数列倒序排列的时候，所以使用l l int；
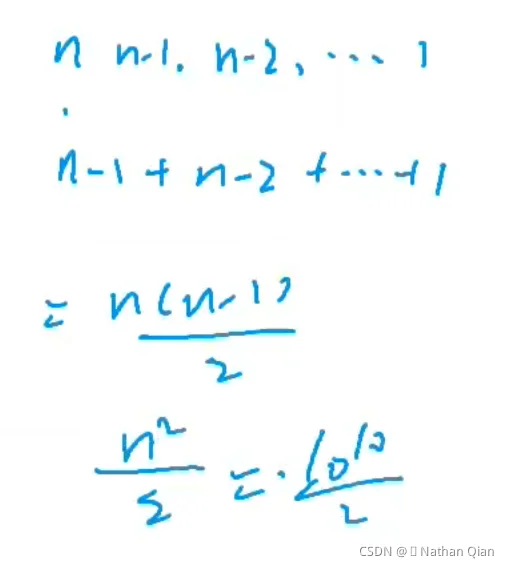
代码段注释：
一开始递归到区间为1（左右两边）的情形，排序好第二层左右两边的内容
当返回进入n层的时候有两个任务
第一个任务（在n-1层的时候已经做完）检查递归排序好左边和右边（抽象意义，实际没有检查）
第二个任务为（完成第一任务前提下）对左右边进行比较，满足逆序对情形则记录res的值；
这里可以res表达式的原因是
到第n层因为左边和右边的都已经在第n - 1层的时候排序好
所以在进行第n层的比较时，直接输出mid - i + 1
L mergesort(int l, int r)
{
if (l == r)return 0;
int mid = l + r >> 1;
L res = mergesort(l, mid) + mergesort(mid + 1, r);
归并的过程
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
if (a[i] <= a[j])tmp[k++] = a[i++];
else
{
tmp[k++] = a[j++];
res += mid - i + 1;
}
扫尾
while (i <= mid)tmp[k++] = a[i++];
while (j <= r)tmp[k++] = a[j++];
物归原主
for (int i = l, j = 0; i <= r; i++, j++)a[i] = tmp[j];
return res;
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++)cin >> a[i];
cout << mergesort(0, n - 1) << endl;
}
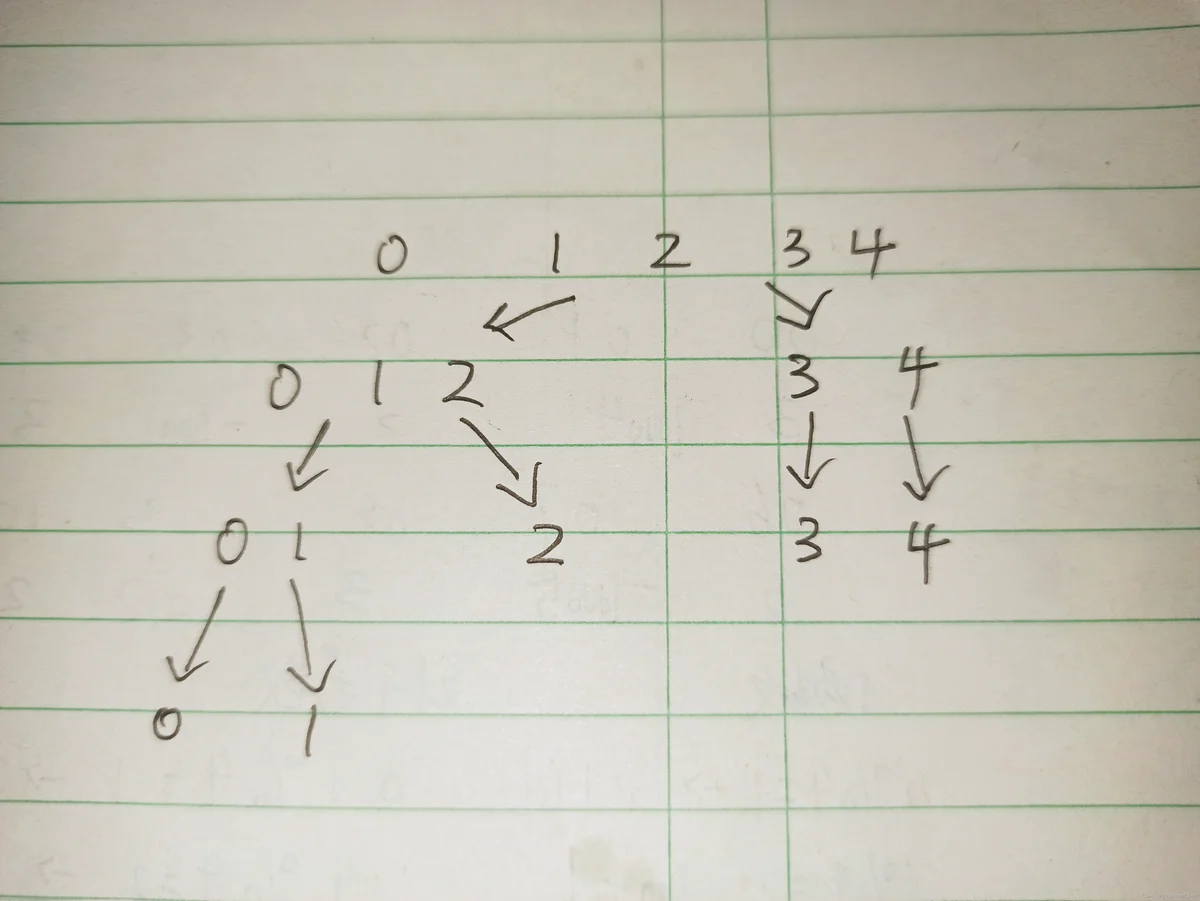
如图所示完成递归到底层后，例如左边的0，1（这里数字代表元素的下标）
递归执行顺序为：0->01->1->01(res)->012->2->012(res)........(类推）