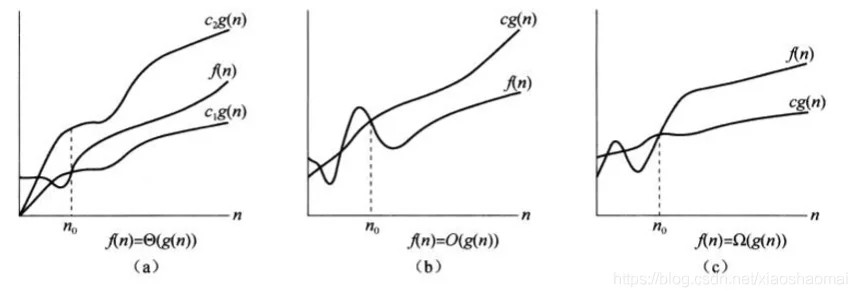
渐进紧确
类似于高数里面极限和夹逼定理的概念,忽略低阶项,用于时间复杂度表示(一般取上限),不需要深究,了解几个符号就行:

插入排序
思想:
想象成抽牌,左边是手上的牌,右边是牌堆,从右边不断抽取牌,并且同坐边一一比较,发现合适的位置就插入。时间复杂度:n~n^2;空间复杂度:1
难点:
查找到比自己小的数或者循环到-1时,退出循环,此时计数会-1,因此插入数的时候别忘了+1
func insertSort(arr []int) {
for i := 1; i < len(arr); i++ {
temp := arr[i] //用来存要插入的数
j := i - 1 //不能用局部变量,因为最后插入要参考这个索引
for ; j >= 0 && temp < arr[j]; j-- {
arr[j+1] = arr[j] //如果插入数字比切片里的数小,就把切片数字向后移腾位置,否则跳出循环
}
arr[j+1] = temp //+1是因为循环最后j--,如果不发生循环,插入就是自己位置,j=i-1所以还是要+1,秒啊
}
}
归并排序
思想:
分治法,先把问题划分为子问题,子问题继续划分,直到可以解决,之后用同种方法解决父问题,直到全部解决。排序就是将数组一分为二、二分为四…直到分成一堆长度为1的“数组”,之后同父分出来的子数组两两比较,排出顺序父数组;父数组和伯数组比较,排出顺序爷数组…最终全部排出来。时间复杂度为cn(lgn+1)
难点:
归和并可以拆开来写方法,并的时候注意一个数组结束之后,就不再比较,直接把另一个数组贴在尾巴上即可,避免数组越界!
//合并两个数组,索引分别为p~q,q+1~r
func merge(arr[]int, p,q,r int){
temp:=make([]int,len(arr))
copy(temp,arr)//用temp保持原有的顺序用来比较,比较后填入arr中
i:=p//前切片索引
j:=q+1//后切片索引
k:=p//空切片索引
for ;k<=r;{
//谁小先把谁填入数组
if temp[i]<=temp[j] {
arr[k]=temp[i]
k++
i++
}else{
arr[k]=temp[j]
k++
j++
}
//如果前面的先填完了,后面剩下的就统一填进去
if i>q {
for ;j<=r;j++{
arr[k]=temp[j]
k++
}
}
//同理后面整完了,前面剩下的统一填进去
if j>r {
for ;i<=q;i++{
arr[k]=temp[i]
k++
}
}
}
}
用递归来切分数组,递归终止条件,切片长度为1(索引相等),即可开始调用merge方法来比较。q取中位数的时候,不论长度是奇数还是偶数,都是前一段数组的最后一个数
func merge_sort(arr[]int, p,r int){
if p < r {
var q int
q = (p + r) / 2
merge_sort(arr, p, q) //前一段继续分
merge_sort(arr, q+1, r) //后一段继续分
merge(arr, p, q, r) //比较两段,按顺序合并成一段
}
}
冒泡排序
思想:
冒泡排序,就是和依次和后面的比大小,前大后小就交换,顺序遍历一遍切片之后,最大的数字就像泡泡一样冒到最后,之后就对n-1长度的切片遍历,依次类推。可以发现需要遍历n ^2次,时间复杂度为 n ^2。算法较笨,适合简单的排序
难点:
冒泡一次就有一个数排在了最后(最前),再遍历切片就不用啦!golang变量交换真容易
func bubblingSort(a []int) {
for i := 0; i < len(a)-1; i++ {
for j := 0; j < len(a)-i-1; j++ {//遍历长度逐渐缩短哟
if a[j] > a[j+1] {
a[j], a[j+1] = a[j+1], a[j]
}
}
}
}
快速排序
思想:
还是用的分治思想,想想归并是等分两份再去排那两份,但是呢,这么分就仅仅是吧问题除以2,并没有在分的过程中,做一些工作吧(太懒了,光去想着分小,不想着每次解决一些问题)。那么,在每次分的过程中,是不是可以把大的放后面,小的放前面呢,这样就初步有个顺序了,显然比归并算法效率更高(不至于前面一堆方差贼大的数,后面一堆平均值附近的数,那样合并的时候真是头疼),这样合并的时候,小的在后大的在前,减少了很多运算时间。虽然和归并算法一样,时间复杂度为O(nlgn),而且最坏情况还是n^2,但是基本不会发生最坏情况,期望时间复杂度好,所以比归并排序应用更广泛。
难点:
在原数组上进行排序,不需要新的内存,只需要一个temp存放基准
func quickSort(A []int, low, high int) {
//终止条件,左右索引相等,只有一个数时截止
if low < high {
q:=partition(A,low,high)//索引q上的数为分界点,左边均小于A[q],右边均大于A[q]
//在左右子数组上继续快排,分治思想
quickSort(A,low,q-1)
quickSort(A,q+1,high)
}
}
//把数组第一个数作为基准进行排序,排序结果,左边都小于基准,右边都大于基准,返回基准的索引
func partition(A[]int,low,high int)(q int){
temp := A[low]//选定基准,相当于low地方是一个空位(想象成把上面的数挖走了)
for low < high {
//先从高往低遍历,找一找谁小于基准,小于基准的话就别呆在右边了,去前面那个坑吧(他走了高位就留下一个坑了)
for ;high>low&&A[high]>temp;{
high--
}
//填坑的时候一定要判断索引是否合法,如果相等了就不填坑(哪有自己填自己的)
if low<high{
A[low]=A[high]
low++//前面的都是小于基准
}
//填完之后再从前往后找一个,找到一个大于基准的数,让他填高位的坑
for ;low<high&&A[low]<temp;{
low++
}
if low<high{
A[low]=A[high]
high--//后面的都是大于基准
}
}
A[low]=temp//最后一个坑由基准来填,大小就由此分界
return low//返回分界线
}
堆排序
思想:
建最大堆进行排序,每次调整完的堆顶是最大值,换到最后,再进行调整,循环往复。排序时间复杂度为O(nlogn),建堆时间复杂度为O(n),需要用无穷级数来证明,比较麻烦;调整时间复杂度为O(lgn),主定理可以证明。
难点:
每次调整堆的时候,需要把堆的长度减少1,因为最后那个数时排序好的,不能动它;注意左右子堆的索引是l:=2i+1和r:=2i+2,不要弄错了
//维护堆的性质,给定根索引,如果不是最大堆,则调整,时间复杂度O(lgn)
func maxHeapify(A[]int,i,len int){
l:=2*i+1
r:=2*i+2
var max int
//看看左子节点和根谁大
if l<len&&A[l]>A[i]{
max=l
}else {
max=i
}
//再和右子节点比比谁大
if r<len&&A[r]>A[max]{
max=r
}
//如果根不是最大,则和最大交换
if max!=i{
A[max],A[i]=A[i],A[max]
maxHeapify(A,max,len)//既然换了,这个子堆也要进行最大堆化的调整
}
}
//建堆,时间复杂度为O(n)
func buildMaxHeap(A[]int){
for i:=(len(A)-1)/2;i>=0;i--{
maxHeapify(A,i,len(A))
}
}
//堆排序,时间复杂度为O(nlgn)
func heapSort(A[]int){
buildMaxHeap(A)//初始化建堆
fmt.Println(A)
for i:=len(A)-1;i>0;i--{
A[i],A[0]=A[0],A[i]//把最大值交换最后
maxHeapify(A,0,i)//重新调整堆使其变成最大堆
fmt.Println(A)
}
}
计数排序
思想:
构建辅助数组C,其大小为排序数组A值的range,之后将辅助数组C的索引看成是排序数组A的值,辅助数组C索引对应的值即排序数组A中有该索引大小值得个数。(例如A{1,1,3,2,2,2},其对应的C{0,2,3,1}),之后便容易得到每个数排在它前面数的总数,即该数在数组中应该排的位置。时间杂度为θ(k+n),当k<=0时,时间复杂度为θ(n)
难点:
注意最后输出的时候需要从后往前输出,这样才是稳定的。否则相等的数在排序前后会调换位置。
func countingSort(A[]int,k int)[]int{
B:=make([]int,len(A))
C:=make([]int,k)
for i:=0;i<len(A);i++{
C[A[i]]=C[A[i]]+1
}
for i:=1;i<k;i++{
C[i]+=C[i-1]
}
for i:=len(A)-1;i>0;i--{
B[C[A[i]]-1]=A[i]
C[A[i]]-=1
}
return B
}
桶排序
思想:桶排序和技术排序思想一样,区别是给辅助数组固定长度,而辅助数组中一个区间里可以存储多个不同数据,以链表形式表现,最后每个链表取出来依次连在一起。
难点:每个桶的大小怎么计算?尤其是最大最小值不能排除在桶之外。除此之外,每个桶内还要进行排序。
type list struct {
array []int
index int
}
func (l *list)Init(length int){
l.array=make([]int,length)
l.index=0
}
func (l *list)Add(x int) {
l.array[l.index]=x
l.index++
if l.index>1{
insertSort(l.array,l.index)
}
}
func bucketSort(A[]int,bucket int) []int{
min:=int(^uint(0)>>1)
max:=^min
for i:=0;i<len(A);i++{
if A[i]<min{
min=A[i]
}
if A[i]>max{
max=A[i]
}
}
B:=make([]list,bucket)
for i:=0;i<bucket;i++{
B[i].Init(bucket)
}
base:=(max-min)/bucket+1
for i:=0;i<len(A);i++{
j:=(A[i]-min)/base
B[j].Add(A[i])
}
ai:=0
for i:=0;i<bucket;i++{
for j:=0;j<B[i].index;j++{
A[ai]=B[i].array[j]
ai++
}
}
return A
}
func insertSort(arr []int,sortlen int) {
for i := 1; i < sortlen; i++ {
temp := arr[i] //用来存要插入的数
j := i - 1 //不能用局部变量,因为最后插入要参考这个索引
for ; j >= 0 && temp < arr[j]; j-- {
arr[j+1] = arr[j] //如果插入数字比切片里的数小,就把切片数字向后移腾位置,否则跳出循环
}
arr[j+1] = temp //+1是因为循环最后j--,如果不发生循环,插入就是自己位置,j=i-1所以还是要+1,秒啊
}
}
求最大子数组
思想:
怎么分?二分这么对称当然是用它了,分成两部分找最大连续子数组是不是比原来容易一些,那分完怎么找?要么在前半部分,要么在后半部分,要么前后都有,中间切点连起来就是。有了这个思路,就可以为所欲为的一直分下去,终止条件就是分成长度为一的数组了。
难点:
需要考虑什么参数呢,对比归并,肯定是前后两个索引不能少,数组本身也得传递下去(不然拿着索引没用啊),那切点也得有吧,不然我怎么分呢?返回什么数呢,前后索引肯定要有,因为要确定子数组的位置,切片就不用返回了,因为本来就有,最大子数组起码把最大值返回来吧。那就确定函数这么写:
func findMaxSub(arr []int, low, high int) (rLow, rHigh, result int) {
//停止条件:只有一个数字
if high == low {
return low, high, arr[low] //只有本身一个子数组,子数组之和为自己本身
}
mid := (low + high) / 2
leftLow, leftHigh, leftResult := findMaxSub(arr, low, mid) //分解去前半段找
rightLow, rightHigh, rightResult := findMaxSub(arr, mid+1, high) //分解去后半段找
crossLow, crossHigh, crossResult := findMaxCrossingSub(arr, low, mid, high) //包含中间的情况
if leftResult>=rightResult&&leftResult>=crossResult{
return leftLow,leftHigh,leftResult
} else if rightResult>=crossResult&&rightResult>=leftResult {
return rightLow,rightHigh,rightResult
} else {
return crossLow,crossHigh,crossResult
}
}
可以看到,如果最大子数组在左右两边的话直接分下去找就完事了,递归本方法,那如果在中间可咋办啊。那就从中间到两边分别取遍历呗,定了中间点,去两边找是不是简单很多,弄一个全局变量比大小,最后左右分别确定俩位置,把总和一加就成,参考findMaxCrossingSub函数:
//假定子数组必然包含中点的情况,找出左右索引和子数组之和
func findMaxCrossingSub(arr []int, low, mid, high int) (maxLeft, maxRight, result int) {
leftSum := ^int(^uint(0) >> 1)
sum := 0
//遍历左边找到最大子数组和
for i := mid; i >= low; i-- {
sum = sum + arr[i]
if sum > leftSum {
leftSum = sum
maxLeft = i
}
}
rightSum := ^int(^uint(0) >> 1)
sum = 0
//遍历右边找到最大子数组和
for i := mid + 1; i <= high; i++ {
sum = sum + arr[i]
if sum > rightSum {
rightSum = sum
maxRight = i
}
}
return maxLeft, maxRight, leftSum + rightSum
}
矩阵相乘
思想:
矩阵四等分成子矩阵,子矩阵根据乘法再求和,典型的分治法。
难点:
拆分合并矩阵真的麻烦的要死,strassen方法需要数学证明太麻烦了,分治法只用看看这种就行。(目前只能算2的整数次幂的举证,非整数拆出来还不是方阵,以后有空改吧,分治思想掌握就行)
//蛮力法
func squareMatrixMultiply1(A, B [][]int) (C [][]int) {
C = make([][]int, len(A))
for i, _ := range C {
C[i] = make([]int, len(B[0]))
}
for i := 0; i < len(A); i++ {
for j := 0; j < len(B[i]); j++ {
for k := 0; k < len(B); k++ {
C[i][j] += A[i][k] * B[k][j]
}
}
}
return C
}
//分治法
func squareMatrixMultiply2(A, B [][]int, n int) (C [][]int) {
//初始化矩阵C
C = make([][]int, n)
for i, _ := range C {
C[i] = make([]int, n)
}
if n == 1 {
C=squareMatrixMultiply1(A,B)
return C
}
if n > 1 {
m := n / 2
A1 := divideMatrix(A, 1, 1)
A2 := divideMatrix(A, 1, 2)
A3 := divideMatrix(A, 2, 1)
A4 := divideMatrix(A, 2, 2)
B1 := divideMatrix(B, 1, 1)
B2 := divideMatrix(B, 1, 2)
B3 := divideMatrix(B, 2, 1)
B4 := divideMatrix(B, 2, 2)
C1 := addTwoMatrix(squareMatrixMultiply2(A1, B1, m), squareMatrixMultiply2(A2, B3, m), m)
C2 := addTwoMatrix(squareMatrixMultiply2(A1, B2, m), squareMatrixMultiply2(A2, B4, m), m)
C3 := addTwoMatrix(squareMatrixMultiply2(A3, B1, m), squareMatrixMultiply2(A4, B3, m), m)
C4 := addTwoMatrix(squareMatrixMultiply2(A3, B2, m), squareMatrixMultiply2(A4, B4, m), m)
C = togetherMatrix(C1, C2, C3, C4, m)
}
return C
}
//截取A11 A12 四个子矩阵
// A21 A22
func divideMatrix(A [][]int, x, y int) (C [][]int) {
a := len(A) / 2
if x == 1 && y == 1 {
for i := 0; i < a; i++ {
C = append(C, A[i])
C[i] = C[i][:a]
}
}
if x == 1 && y == 2 {
for i := 0; i < a; i++ {
C = append(C, A[i])
C[i] = C[i][a:]
}
}
if x == 2 && y == 1 {
for i := a; i < len(A); i++ {
C = append(C, A[i])
C[i-a] = C[i-a][:a]
}
}
if x == 2 && y == 2 {
for i := a; i < len(A); i++ {
C = append(C, A[i])
C[i-a] = C[i-a][a:]
}
}
return C
}
//四个子矩阵拼接成一个矩阵
func togetherMatrix(a, b, c, d [][]int, n int) (C [][]int) {
C = make([][]int, 2*n)
for i, _ := range C {
C[i] = make([]int, 2*n)
}
for i := 0; i < 2*n; i++ {
for j := 0; j < 2*n; j++ {
if i < n {
if j < n {
C[i][j] = a[i][j]
} else {
C[i][j] = b[i][j-n]
}
} else {
if j < n {
C[i][j] = c[i-n][j]
} else {
C[i][j] = d[i-n][j-n]
}
}
}
}
return C
}
//两个矩阵相加
func addTwoMatrix(A, B [][]int, n int) (C [][]int) {
C = make([][]int, n)
for i, _ := range C {
C[i] = make([]int, n)
}
for i := 0; i < n; i++ {
for j := 0; j < n; j++ {
C[i][j] = A[i][j] + B[i][j]
}
}
return C
}
数组第i小的数
思想:用到快速排序的思想,但是每次舍弃不用的一边,这样减少了运算复杂度,不需要给数组排序就能找出某个特定位置的数,其渐进运行时间为θ(n)
func random(A[]int,low,high int)int{
temp:=A[low]
for low<high{
for high>low&&A[high]>temp{
high--
}
if high>low{
A[low]=A[high]
low++
}
for low<high&&A[low]<temp{
low++
}
if low<high {
A[high]=A[low]
high--
}
}
A[low]=temp
return low
}
func randomSelect(A[]int,p,q,i int)int{
if p==q{
return A[p]
}
ran:=random(A,p,q)
if ran-p+1==i{
return A[ran]
}else if ran-p+1<i {
return randomSelect(A,ran+1,q,i-(ran-p+1))
}else {
return randomSelect(A,p,ran-1,i)
}
}
