【LeetCode】No.5. Longest Palindromic Substring

题目链接： https://leetcode.com/problems/longest-palindromic-substring/

1. 题目介绍（最长回文子串）

Given a string s, return the longest palindromic substring in s.

【Translate】： 给定一个字符串s，返回s中最长的回文子字符串。

测试用例：

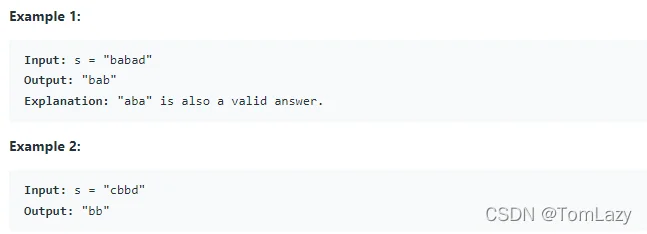
约束：

2. 题解

2.1 暴力枚举 – O(n^3)

  暴力枚举无论在哪，永不褪色！但就是由于执行次数太多，速度太慢。不过它的做法还是非常简单的，首先我们可以将如何判断一个字符串是否是回文封装成一个函数，然后借助substring()方法来分割子字符串（假设s为“abcdcba”，那么整个序列就是"a"、"ab、“abc”……“b”、“bc”……“ba”、“a”），把所有可能的子串全部判断一遍，然后找出其中最长的子串进行返回。

class Solution {public int IsPalindrome(String A){char[] arrayA = A.toCharArray();int top = 0;int end = arrayA.length-1;if(A.equals("") || A.equals(null))    //非法输入return 0;while(top < end){if(arrayA[top++] != arrayA[end--])return 0;}return A.length();}public String longestPalindrome(String s) {int subLen = 0;int maxLen = 0;String maxStr = "";if(s.length() == 1){return s;}for(int i = 0; i < s.length(); i++){for(int j = i+1; j <= s.length(); j++){subLen = IsPalindrome(s.substring(i, j));// System.out.println(s.substring(i, 2));if(subLen > maxLen){maxLen = subLen;maxStr = s.substring(i, j);}}}return maxStr;}
}

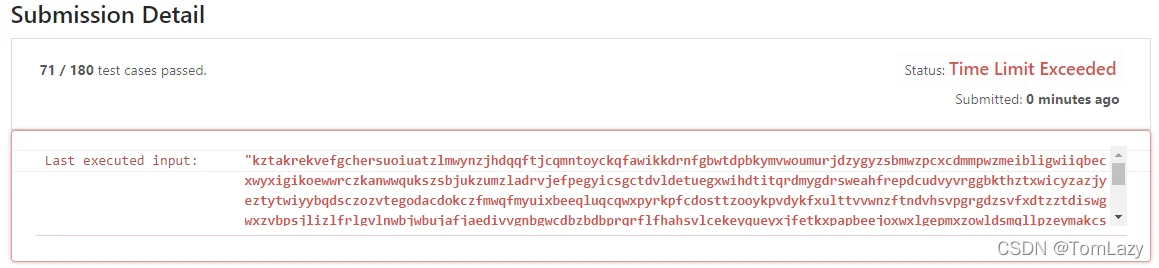
暴力枚举优化

class Solution {public String longestPalindrome(String s) {char[] charArray = s.toCharArray();int start = 0;int maxLen = 0;for (int i = 0; i < charArray.length; i++) {for (int len = 0; i + len < charArray.length; len++) {if (isPalindrome(charArray, i, len) && len + 1 > maxLen) {maxLen = len + 1;start = i;}}}return s.substring(start, start + maxLen);}public boolean isPalindrome(char[] charArray, int start, int len) {while (len > 0) {if (charArray[start] != charArray[start + len]) {return false;}start++;len -= 2;}return true;}
}

2.2 n次遍历选最大 – O(n^2)

ii

    private int lo, maxLen;public String longestPalindrome(String s) {int len = s.length();if (len < 2)return s;for (int i = 0; i < len-1; i++) {extendPalindrome(s, i, i);  //assume odd length, try to extend Palindrome as possibleextendPalindrome(s, i, i+1); //assume even length.}return s.substring(lo, lo + maxLen);}private void extendPalindrome(String s, int j, int k) {while (j >= 0 && k < s.length() && s.charAt(j) == s.charAt(k)) {j--;k++;}if (maxLen < k - j - 1) {lo = j + 1;maxLen = k - j - 1;}}

2.3 递归 – O(n^3)

  递归的作用，大多还是用于简化代码，让语句变得干净一些。这是ande_ka_funda提供的题解，其本身的时间复杂度差不多也是O(n^3)，所以如暴力枚举一般，也会存在超时的情况。

class Solution {public String longestPalindrome(String s) {int len = s.length();int maxLen = 0;String res = "";for (int left = 0; left < len; left++){for (int right = left; right < len; right++){if (s.charAt(left) == s.charAt(right) && isPalin(s,left + 1, right -1)){if (maxLen < right - left + 1) {maxLen = right - left + 1;res = s.substring(left, right + 1);}}   }}return res;}public boolean isPalin(String s, int left, int right){if (left >= right){return true;}if (s.charAt(left) != s.charAt(right)) {return false;}if (right - left <= 2){return true;}return isPalin(s,left + 1, right - 1);}}

自顶向下 dp：

class Solution {Boolean[][] memo ;public String longestPalindrome(String s) {int len = s.length();int maxLen = 0;String res = "";memo = new Boolean[len][len];for (int left = 0; left < len; left++){for (int right = left; right < len; right++){if (s.charAt(left) == s.charAt(right) && isPalin(s,left + 1, right -1)){if (maxLen < right - left + 1) {maxLen = right - left + 1;res = s.substring(left, right + 1);}}   }}return res;}public boolean isPalin(String s, int left, int right){if (left >= right){return true;}if (memo[left][right] != null){return memo[left][right] ;}if (s.charAt(left) != s.charAt(right)) {memo[left][right] = false;return memo[left][right];}if (right - left <= 2){memo[left][right] = true;return memo[left][right];}memo[left][right] = isPalin(s,left + 1, right - 1);return memo[left][right];}}

自下而上 dp：

class Solution {boolean[][] memo ;public String longestPalindrome(String s) {int len = s.length();int maxLen = 0;String res = "";memo = new boolean[len][len];for (int left = len -1; left >= 0; left--){ // notice this goes backwardsfor (int right = left; right < len; right++){if (s.charAt(left) == s.charAt(right)){if (right - left <=2){memo[left][right] = true;} else{memo[left][right] = memo[left + 1][right - 1]; }}if (memo[left][right]  && maxLen < right - left + 1) {maxLen = right - left + 1;res = s.substring(left, right + 1);}}   }return res;}}

2.4 其它方法

Solution中提到的其它解法

• Expand Around Center：O(n^2)
• Manacher’s Algorithm：O(n)

3. 可参考

[1] 【面试现场】如何找到字符串中的最长回文子串？
[2] Java 判断字符串是否是回文字符串
[3] java判断回文字符串的几种方法
[4] java取字符串前几位字符
[5] Java 获取字符串指定下标位置的值 charAt()
[6] Java字符串处理之返回指定字符串下标（indexOf）