最近一直在学习差分隐私，刚开始学的时候由于对这方面的知识不太清楚，一直处于模模糊糊的理解状态。现在学习了一段时间后开始有了一些初步的认识，所以把学习过程中的一些知识总结一下，方便以后复习，也为其他的小伙伴提供一些思路。由于我也是初学者，所以难免会出现一些错误，希望各位大佬可以指出。

DworkThe Algorithmic Foundations of Differential Privacy

整体的逻辑是按照三部分展开：

  • 什么是差分隐私，利用一个简单例子形象说明
  • 差分隐私的第一种形式，严格差分隐私
  • 差分隐私的第二种形式，松弛差分隐私
  • 附：符号的一些说明

1 - 什么是差分隐私

差分隐私差分攻击差分攻击
图1-1 差分攻击示意图

这里张三作为一个样本的的出现，使得攻击者获得了奇怪的知识。而差分隐私需要做到的就是使得攻击者的知识不会因为这些新样本的出现而发生变化。

那怎么做到呢？加入随机噪声。比如刚才的例子，本来两次查询结构是确定的2和3，现在加入随机噪声后，变成了两个随机变量，画出它们概率分布图。

图1-2 概率分布图

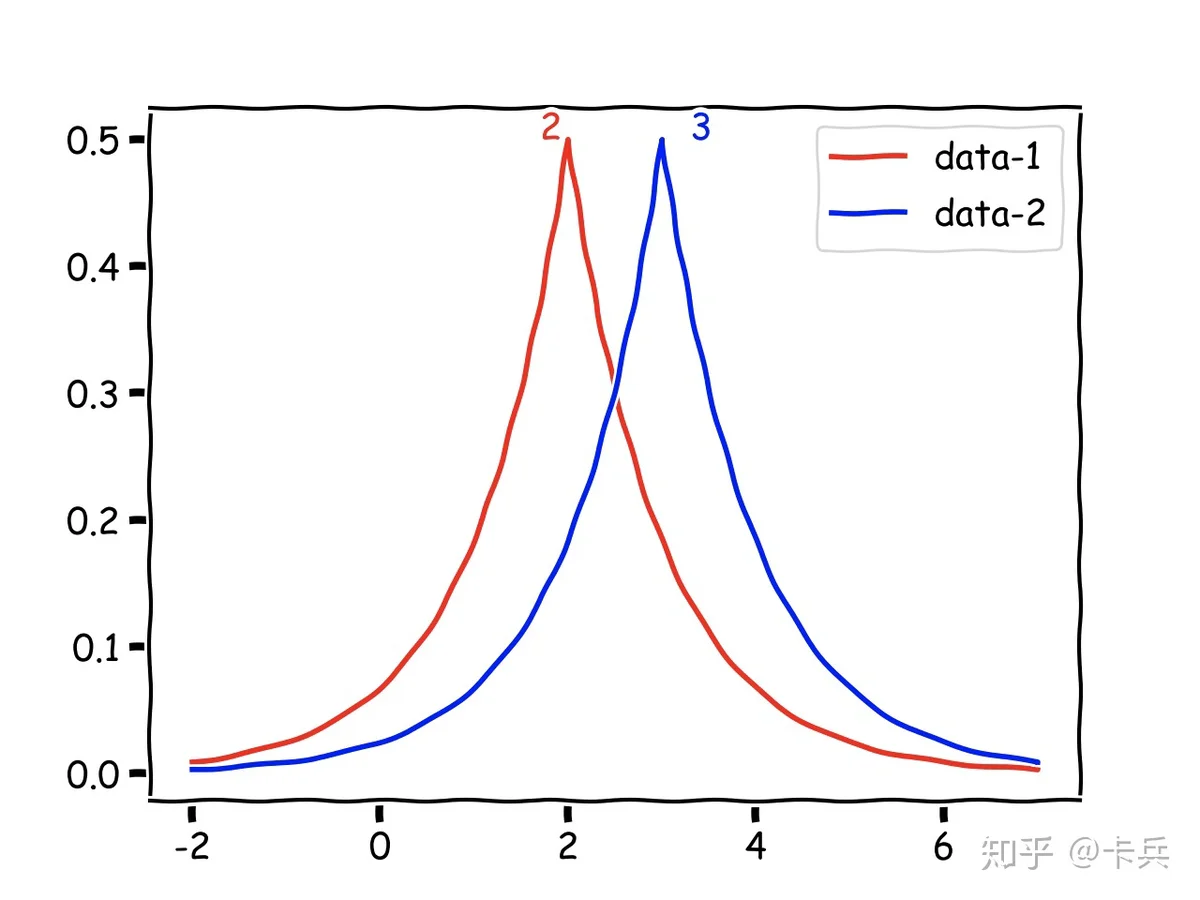
现在，如果张三不在数据库的话，得到结果可能是2.5；张三在的话，得到的结果也可能是2.5；两个数据集查询得到某一个结果的概率很接近，以至于我们根本分不清这个结果来自于哪一个数据集，这样也就实现了攻击者的知识不会因为张三这个样本的出现与否而发生变化。

这些只是概念上的理解，总结一下就是对查询的结果加入噪声，使得攻击者无法辨别某一样本是否在数据集中。一个形象的说法就是，双兔傍地走安能辨我是雄雌。

2 - 公式化的理解

刚才只是讲到概念上的理解，现在从数学上理解一下。上面的查询函数可以用 f(x):x\rightarrow R 表示（这里暂时只考虑输出结果为1维的情况），随机噪声可以用 r 表示，最终得到的查询结果就是 \mathcal{M}(x)=f(x)+r ，对于两个汉明距离为1的数据集 x,x' ，对于任意的输出集合 S ，应该有：

图2-1 差分隐私定义
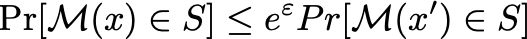
The Algorithmic Foundations of Differential Privacy3.5.1
KL-Divergence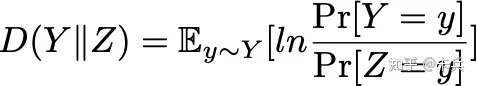
MAX-Divergence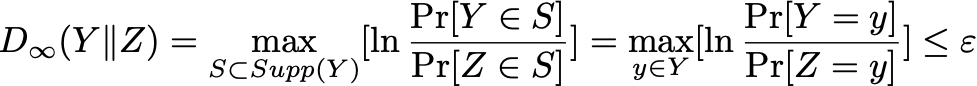

化简一下，利用 e 指数运算将 \ln 符号消去，然后将左边分母移到右边，就可以得到最开始的图2-1 差分隐私定义中定义的内容了。

Max-Dvergence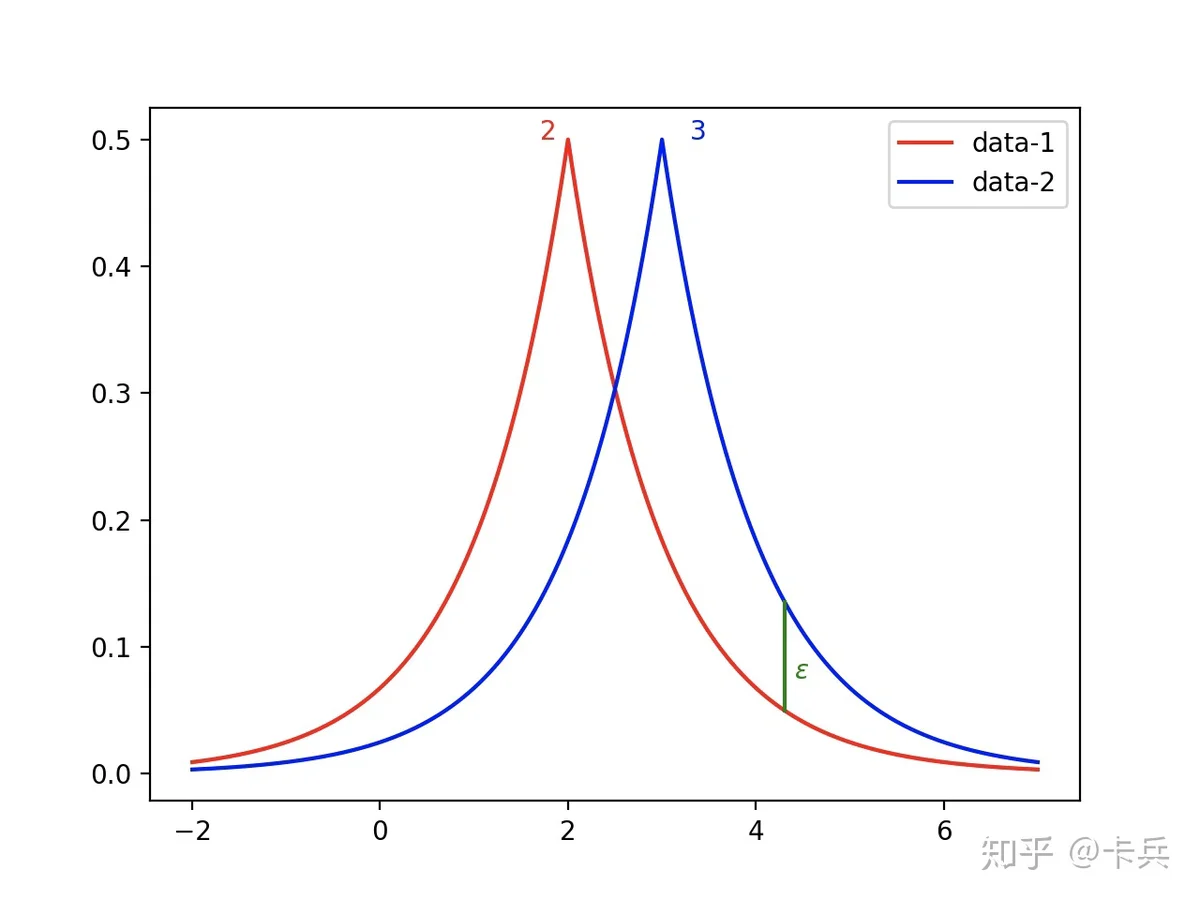
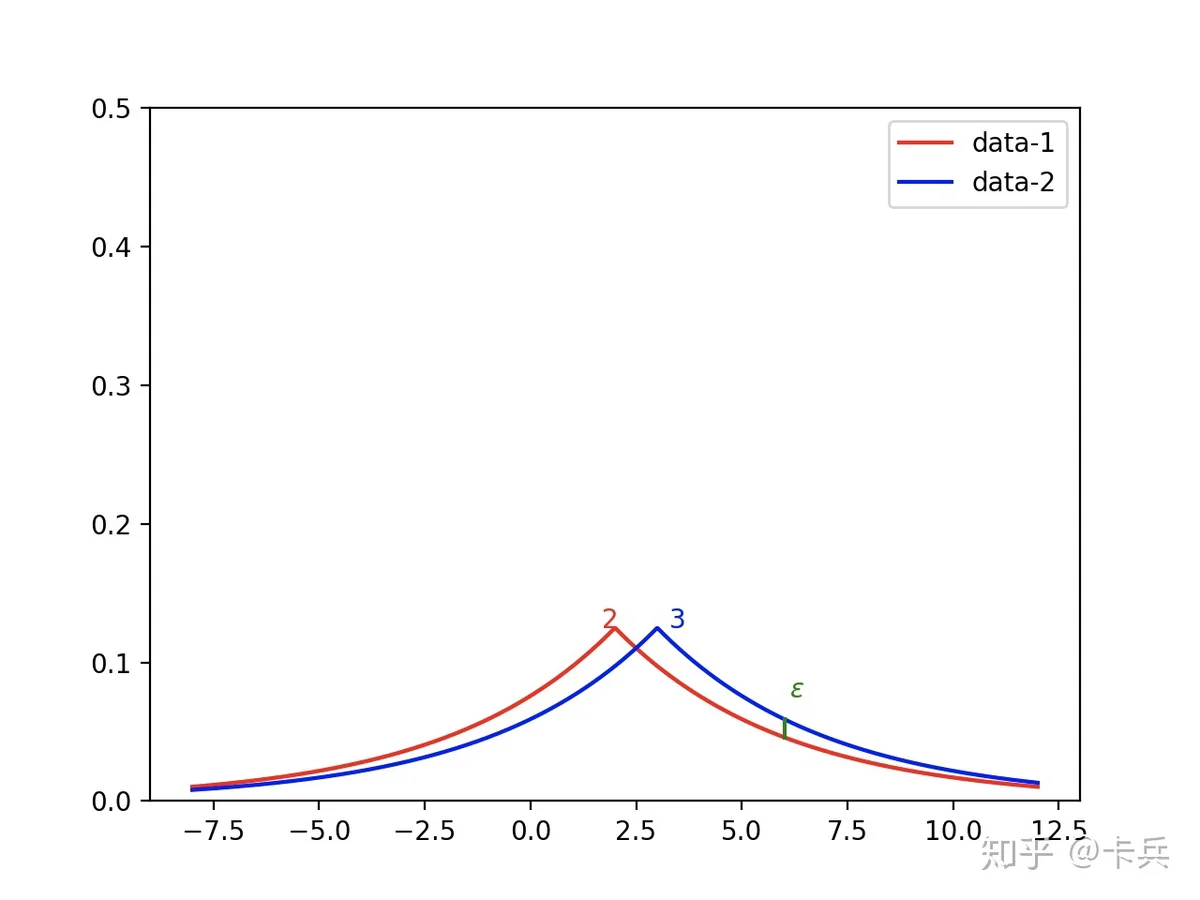
图 2-2 bound住Max-divergence

而 \varepsilon 就被称为隐私预算，一般而言， \varepsilon 越小，隐私保护越好，但是加入的噪声就越大，数据可用性就下降了，如下图2-3，数据相对于正确的中心值更加分散。对于应用差分隐私的算法，首先会设定整体的隐私预算，每访问一次数据，就会扣除一些预算，当预算用完，数据就无法再访问，

图2-3 更大噪声水平下的概率分布图

3 - 差分隐私的松弛

Dwork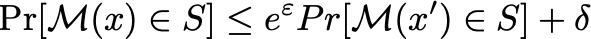
Max-Divergence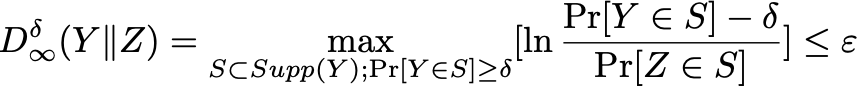

相比较于原始的式子，对分子减去了一个 \delta，也就是说我们可以容忍一个较小的差距。

直观形式如下图，像图中标注的位置，本来 \varepsilon 是无法bound住，但是我们考虑松弛项 \delta ，整体依旧满足差分隐私。一般 \delta 都设置的比较小。

图3-1 松弛差分隐私
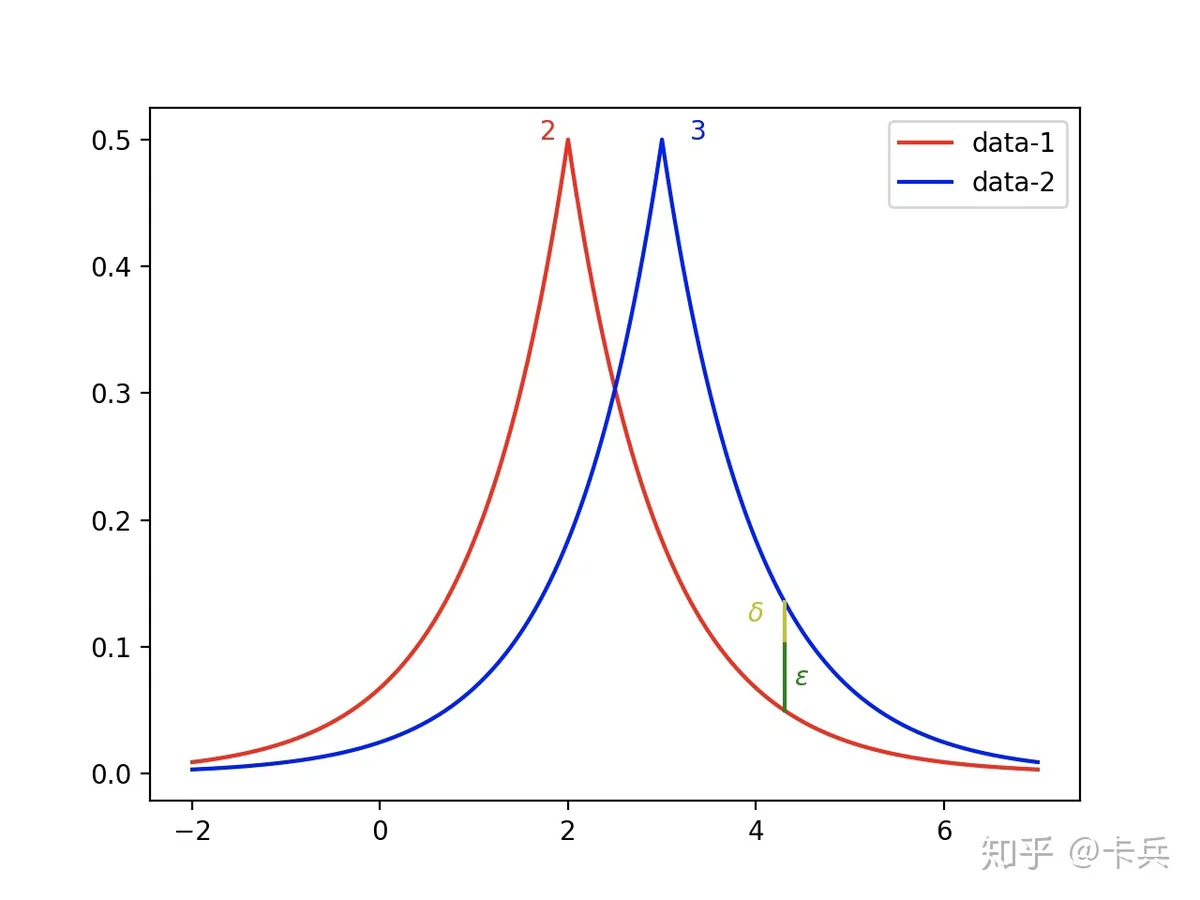
Dwork

4 总结

这篇主要讲的差分隐私概念的来源和形式定义，但是对于差分隐私中的噪声怎么加没有讲，下面应该会去学习差分隐私中Laplace, Exponential, Gaussian三中噪声机制以及对应的证明。

5 符号

  • f(x) 表示一个查询函数，比如查询count值，最大值，均值，梯度等等。
  • R 表示一个实数的概念，上标如果不写表示一维数据，比如最大值；如果是 R^n 表示n维数据，比如梯度。
  • r 表示一个随机噪声，可以服从高斯分布或者指数分布。
  • 兄弟数据及 x,x' 表示两个数据集只相差了一个样本。
  • \mathcal{M}(x) 表示最终的一个确定的查询结果f(x)加上一个不确定的随机噪声r得到的最终结果。
  • \varepsilon 表示一个很小的值，用来衡量隐私预算。 \delta 是一个松弛项，表示可以接受差分隐私在一定程度上的不满足。
  • D_\alpha(\cdot,\cdot) 表示的是Renyi divergence，当 \alpha 取不同值得时候代表不同的Divergence，比如KL-Divergence，Max-Divergence，是衡量两个分布的一种推广形式的表达，下一篇会讲到。

参考