这是笔者最近关于Jinshuo Dong在2019年所提出的f-dp以及Gaussian Differential Privacy理论的学习笔记,包含了笔者自己的一些理解和观点,如有错误还请各位大佬指出~
1. 问题提出
1.1 (ε, δ)-DP与KL-Divergence回顾
(我们在这里假设读者对差分隐私已经有了一定程度的了解)
在DP的提出时我们考虑过,当掌握了足够多(关于模型、数据等)的先验知识后,我们就可以通过模型的输出,来判断原数据集到底是S还是S'(这里S与S'为邻近数据集)。为了避免这一点,我们在考虑给输出加上一定的噪声:
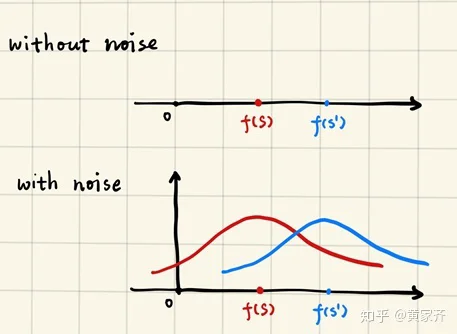
有了噪声之后,我们的模型就从最初的算法f变成了随机算法: M(S) := f(S) + Y ,也就是给输出加上了一个噪声Y,将模型的输出从具体的数值变成了一个随机变量。于是,我们希望M(S)与M(S')这两个随机变量的分布尽可能地接近。
为了量化说明这一点,我们引入了KL-Divergence,用于衡量两个随机变量之间的距离:

我们希望两个变量之间的KL-Divergence尽可能小,因此希望P与Q概率函数比值较小,于是得到了(ε, δ)-DP的定义:

1.2 假设检验的引入和f-dp的提出
那么问题来了,既然我们的目的是将这两个随机变量区分开来,那么为何不直接上统计推断的本质——假设检验呢?我们关注两个随机变量的分布,不就是关心将它们区分开的难易程度吗?我们希望通过两个分布进行假设检验的难度来定义隐私。
我们先大致回顾一下假设检验。如下图,我们有P0和P1两个分布(对应θ0和θ1两个参数),我们需要划定一个拒绝域(见图中x轴上的红线),如果样本落在拒绝域上,我们就拒绝原假设P0,选择备选假设P1。
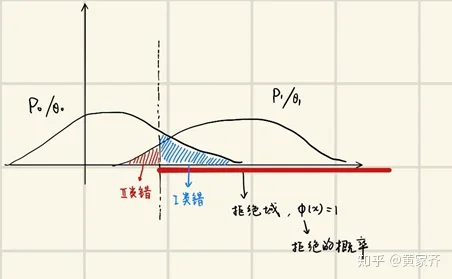
如图中标注的那样,我们有第一类错误,其定义是:原假设正确却被判为错(的概率),以及第二类错误:原假设错误却被判为对(的概率)。随着拒绝域选取的不同,我们会有不同的两类错误。注意到,随着上图中虚线向右移动,我们的第一类错误会减小,第二类错误会增大,反之也能得到相反的结论,于是,两类错误之间其实存在着一个权衡关系(trade off)。
作者由此定义了关于给定显著性水平α的tradeoff函数,并发现这是一项能很好地量化假设检验难度的工具:
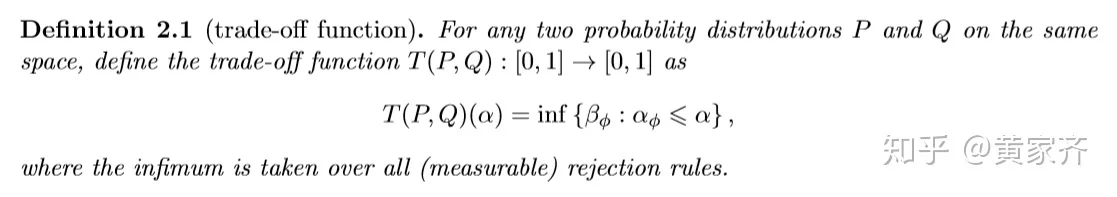
我们可以由此来定义f-DP,这个定义意味着,这个假设检验问题的难度不小于函数f对应的假设检验问题的难度:

这个定义听起来可能有点玄乎,我们可以来看一个例子:
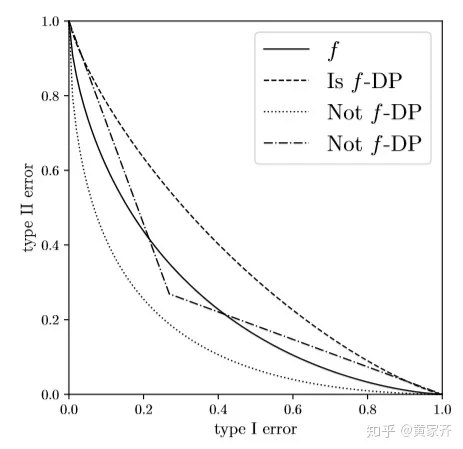
上图中,实线是函数f,则仅有完全在f之上的函数是f-DP的,其他函数都不满足f-DP。
我们下面再给出 G_{μ} 和 G_{μ}-DP 的定义:
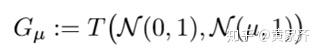
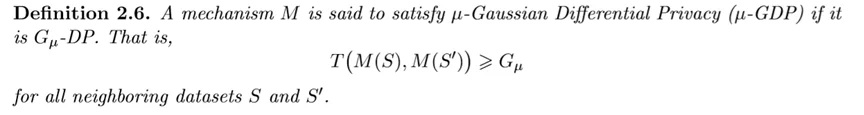
因此,两个分布满足 G{μ}-DP 的意思就是说,通过假设检验区分这两个分布的难度大于区分N(0, 1)、N(μ, 1)的难度,这可以说是一个非常量化的描述了。
下图给出了几个不同μ对应的GDP的例子:
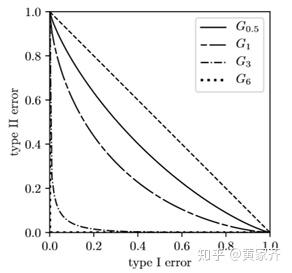
注意到,tradeoff函数越往右上方靠,意味着假设检验的难度就越大,当两个分布相同时,tradeoff函数为 y = 1 - x ,而当tradeoff函数为 y = 1 - x 时,也意味着两个分布(几乎处处)相同,这也可以说是所有tradeoff函数的上界。
2. f-DP及GDP的性质
2.1 tradeoff函数的一些性质
在定义tradeoff函数的时候,我们说,对于任意一个函数g,倘若存在分布P和Q使得 T(P, Q) = g ,我们就将g称作是一个tradeoff函数,否则g就不是tradeoff函数。
于是,我们有关于某一个函数是否是tradeoff函数的充要条件:
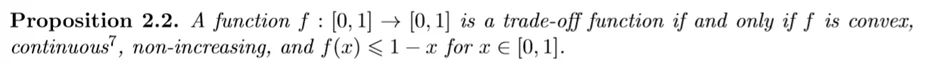
这个结论的证明不难,感兴趣的同学可以去原文看看。
2.2 f-DP和(ε, δ)-DP的联系
接下来介绍一个很关键的性质,我们来看下面这个定理:
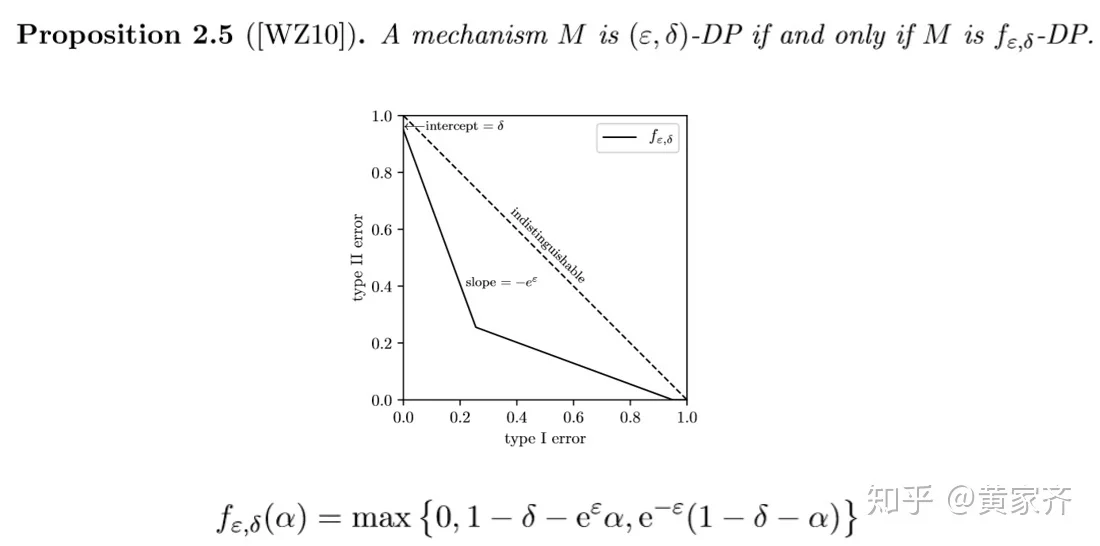
f-DP包含了(ε, δ)-DP!也就是说,任何一组,(ε, δ)-DP都对应着某一个tradeoff函数,(ε, δ)-DP是f-DP的一个特例,或者说是一种特殊情况!相信不必多说,同学们也能get到这一性质的重要性吧。
这个定理的证明是比较简单的,感兴趣的同学可以自己尝试证明一下。
2.3 后处理性质和f-DP的信息含量
直觉上来说,我们希望一个攻击者无法通过对机制M的输出进行处理得到更多有用的信息。这就是后处理性质,是一个对于隐私保护来说非常自然的性质。
我们的f-DP恰好有这样一个性质:
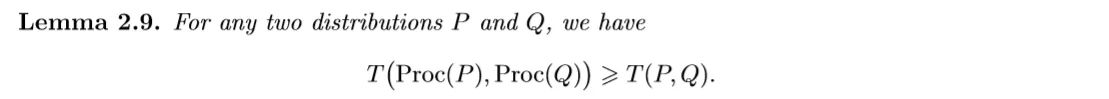
也就是说,如果一个机制M是f-DP的,那么它作用于任意一个后处理之后的 Proc \circ M 也是满足f-DP的。
这个性质源于此处:

(这个部分涉及到高等概率论的内容,下面的内容皆为选读,有兴趣的同学也可以研究一下Blackwell的comparison of experiments。
事实上,post-processing引出了分布对{(P, Q)}之间的一个次序关系,也就是我们可以给其中一些(并非全部,有些分布对之间没有次序关系)不同的分布对来排序,这就是Blackwell order(这个定义在网络资源上找不到,可以参见Blackwell 的comparison of experiments)。也就是说,如果上面的条件(b)满足了,我们就可以记作 (P, Q)\preceq_{Blackwell}(P', Q') ,并且称:在Blackwell意义下, (P, Q) 比 (P', Q') 更容易分辨。类似地,如果有 T(P, Q) \leq T(P', Q') ,我们可以记作 (P, Q)\preceq_{tradeoff}(P', Q') ,并且称:在假设检验意义下,(P, Q) 比 (P', Q') 更容易分辨。
所以说,任何一个关于隐私的度量,都引出了分布对之间的次序关系。我们先前提到,我们希望对隐私的度量可以满足后处理性质,因此,我们希望任何关于隐私的度量至少能大于或者说是包含Blackwell order,这么说有些抽象,我们下面用具体的数学语言来表示一下:
对于一个次序关系,我们可以将它表示为所有可对比的元素对的集合: Ineq(\preceq) = \{(P, Q;P', Q'):(P,Q)\preceq {(P',Q')} \},因此,我们希望我们定义的度量能满足: Ineq(\preceq) \supseteq Ineq(\preceq _{Blackwell}) ,这样的话这个度量就满足了后处理性质。
然而,我们也不希望我们的 Ineq(\preceq) 太大,因为次序关系大了,含有的信息量就少了。譬如说,我们可以定义一个trival divergence: D_0 (P || Q) \equiv 0 ,这样的 Ineq(\preceq _{D_0}) 集合是最大的,但是它几乎没有含有任何信息量。
因此,我们希望我们定义的度量是在 Ineq(\preceq_{D_0}) 和 Ineq(\preceq_{Blackwell}) 之间的。值得注意的是,我们的f-DP,正好满足: Ineq(\preceq _{tradeoff}) = Ineq(\preceq_{Blackwell}) ,因此,f-DP可以说是在这个意义下最好的隐私定义了。作为对比,renyi-DP和(ε, δ)-DP则没有这样的性质。
2.4 对偶性质
先前我们提到,一个(ε, δ)-DP对应着一个f-DP,而反过来,我们其实有:一个f-DP对应着一族的(ε, δ)-DP,相当于f-DP的一族包络线,具体可以参考下图:
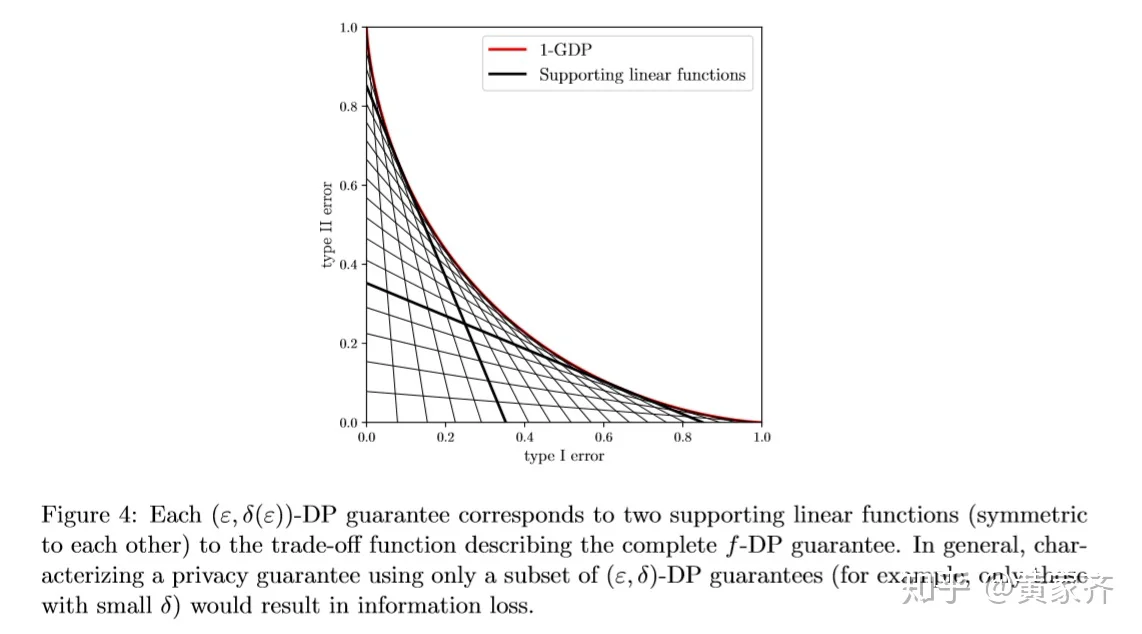
我们在后面的一些证明中会用到这一性质。
3. f-DP的组合(Composition)
在研究DP时,我们很关心几个机制组合(Compose)起来总共泄露了多少隐私,而对于深度学习,我们也很关心联合机制(joint mechanism)的隐私,这个对我们接下来关于SGD的隐私分析是至关重要的。
Martín Abadi等人在Deep Learning with Differential Privacy中,提出了在SGD中进行隐私保护的方法,具体做法是:我们在梯度下降时,先限制住每一个样本的梯度大小(i.e., 用预设的bound C来clip每一个样本的梯度贡献),然后在梯度中注入噪声。注意到,倘若使用这样的方法,那么一个样本的增减对于梯度最多只会带来不大于C的影响,因此在这里C就是我们的敏感度(sensitivity)。下面为此算法的流程图:

之所以有这个扰动梯度的算法,是因为模型的参数和梯度是很容易被攻击者获取的,而我们担心攻击者获取了模型的梯度和参数从而能够分析出用户的信息。
3.1 tradeoff函数的卷积
在这里,我们定义关于两个tradeoff函数的卷积运算,后面我们将用它来计算机制composition的隐私:
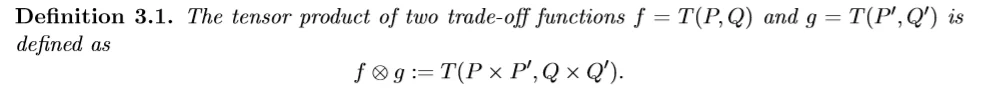
这里具体解释一下,这个卷积是两个tradeoff函数之间的运算,虽然是借助于tradeoff函数对应的分布来定义的,但是与分布的选取无关(事实上,可以有非常多组不同的分布 (P_i, Q_i) 对应着同一个tradeoff函数f),换句话说,不管我们选取 f 对应的哪一组分布 (P, Q) 和 g 对应的哪一组分布 (P', Q') , f 和 g 卷积得到的 f\otimes g 都是相同的,卷积的结果与分布的选取无关。
上述的性质的证明,大家可以在原文的Appendix C中找到。
另外,tradeoff函数的卷积还有一些非常好的性质:

这些性质的证明可以在原文的Appendix D中找到。
根据卷积的定义,我们可以直接得到:
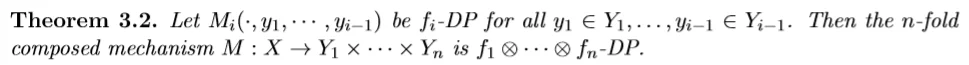
这个定理在说的是,对于同一个数据集,如果我们通过n个机制来获取n次输出,那么总共泄露的隐私可以由n个机制的tradeoff函数的卷积来限制住。
高斯DP的卷积计算是比较容易的:
G_{\mu_1}\otimes G_{\mu_1}\otimes\cdot\cdot\cdot G_{\mu_n} = G_{\mu} ,其中 μ = \sqrt{μ_1^2 + \cdot\cdot\cdot + μ_n^2}
具体证明如下:
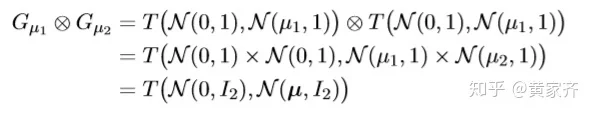

3.1 引理 C.1
这是一个非常关键的引理,蕴含着tradeoff函数以及composition的一些本质的性质。
令 K_{1}, K_{1}^{\prime}: Y \rightarrow Z_{1} 和 K_{2}, K_{2}^{\prime}: Y \rightarrow Z_{2} 为两对随机算法,假设对这四个算法,以下条件成立:对于给定的输入 y\in Y ,假设检验问题 K_{1}(y) \text { vs } K_{1}^{\prime}(y) 的难度要大于 K_{2}(y) \text { vs } K_{2}^{\prime}(y) 的难度,用数学语言来说,记 f_{i}^{y}=T\left(K_{i}(y), K_{i}^{\prime}(y)\right) ,上述的假设就是说 f_{1}^{y} \geqslant f_{2}^{y} 。接下来,我们将输入由固定的y改为随机变量P和P',令 f_{i}=T\left(\left(P, K_{i}(P)\right),\left(P^{\prime}, K_{i}^{\prime}\left(P^{\prime}\right)\right)\right), i=1,2 为联合检验问题的tradeoff函数。由于此时的输入由固定的y改为了P和P',因此输入提供了更多的信息,我们知道两个检验问题都变容易了,即 f_{1} \leqslant f_{1}^{y}, f_{2} \leqslant f_{2}^{y} ,那么 f_1 和 f_2 之间的关系呢?这就引出了我们的引理C.1:
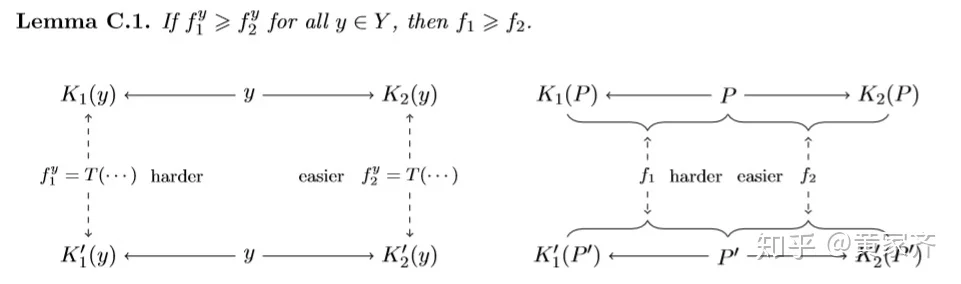
应用这个引理,我们可以很轻易地证明一些性质,比如说,我们想证明3.1的性质2: \text { If } g_{1} \geqslant g_{2}, \text { then } f \otimes g_{1} \geqslant f \otimes g_{2},我们令 f_{i}^{y} = T(P_i, Q_i) = g_i ,令右图的P和P'分别为 f 对应的随机变量P和Q(即 f = T(P, Q) ),就可以直接得到这一不等式。
先记到这里,接下来有空会来填坑~
3.2 f-DP组合的中心极限定理
3.3 与(ε, δ)-DP组合的对比
4. f-DP的降采样
5. f-DP与GDP的应用
5.1 随机梯度下降法的隐私分析
参考
1. J. Dong, A. Roth, and W. J. Su. Gaussian differential privacy. arXiv preprint arXiv:1905.02383, 2019.
2. David Blackwell. Comparison of experiments. Technical report, HOWARD UNIVERSITY Washington United States, 1950.
3. Martin Abadi, Andy Chu, Ian Goodfellow, H Brendan McMahan, Ilya Mironov, Kunal Talwar, and Li Zhang. Deep learning with differential privacy. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, pages 308–318. ACM, 2016.
