冒泡排序
从左到右依次比较两个相邻元素,如果左边元素大于右边元素,就将两者交换;如果左边元素小于等于右边元素,不进行任何操作。
Version1
package main
import "fmt"
func main() {
slice := []int{7, 5, 8, 4, 3, 2, 6, 9, 1}
//执行次数
for i := 0; i < len(slice)-1; i++ {
//比较次数
for j := 0; j < len(slice)-1-i; j++ {
//大于表示升序,小于表示降序
if slice[j] > slice[j+1] {
slice[j], slice[j+1] = slice[j+1], slice[j]
}
}
}
fmt.Println(slice)
}
Version 2:
增加标志位表示切片已经排好序。当flag为true时,直接跳出循环, 也就是当数组接近升序排列时,可以减少循环次数。
package main
import "fmt"
func main() {
slice := []int{7, 5, 8, 4, 3, 2, 6, 9, 1}
for i := 0; i < len(slice)-1; i++ {
var flag = true
for j := 0; j < len(slice)-1-i; j++ {
if slice[j] > slice[j+1] {
slice[j], slice[j+1] = slice[j+1], slice[j]
flag = false
}
}
if flag {
break
}
}
fmt.Println(slice)
}
选择排序
假设数组中第 1 个元素最小,然后让剩余的 N - 1 个元素依次和数组第 1 个元素进行比较,如果比第 1 个元素小,那么就进行交换。然后第2个就是第2小的数,以此类推
Version1:
package main
import "fmt"
func main() {
slice := []int{7, 5, 8, 4, 3, 2, 6, 9, 1}
for i := 0; i < len(slice); i++ {
//用后面的数依次和第一位进行对比,因为j从1开始,进入循环判断时,j已经等于2,所以判断条件不减1
for j := i + 1; j < len(slice); j++ {
if slice[j] < slice[i] {
slice[i], slice[j] = slice[j], slice[i]
fmt.Println(slice)
}
}
}
fmt.Println(slice)
}
Version2:
用变量来维护最小数的索引,在遍历一遍结束后直接交换。
package main
import "fmt"
func main() {
slice := []int{7, 5, 8, 4, 3, 2, 6, 9, 1}
for i := 0; i < len(slice)-1; i++ {
var index = i
for j := i + 1; j < len(slice); j++ {
if slice[j] < slice[index] {
index = j
}
}
slice[index], slice[i] = slice[i], slice[index]
}
fmt.Println(slice)
}
插入排序
在已排序序列中从后向前扫描,找到相应位置并插入。类似于扑克中理牌。
package main
import "fmt"
func main() {
slice := []int{7, 5, 8, 4, 3, 2, 6, 9, 1}
for i := 1; i < len(slice); i++ {
for j := i; j > 0; j-- {
if slice[j] < slice[j-1] {
slice[j], slice[j-1] = slice[j-1], slice[j]
}
}
}
fmt.Println(slice)
}
希尔排序
设定步长,由粗颗粒到细颗粒,当gap为1时,相当于插入排序
package main
import "fmt"
func main() {
slice := []int{7, 5, 8, 4, 3, 2, 6, 9, 1}
gap := len(slice) / 2
for gap >= 1 {
for i := gap; i < len(slice); i++ {
for j := i; j-gap >= 0; j -= gap {
if slice[j] < slice[j-gap] {
slice[j], slice[j-gap] = slice[j-gap], slice[j]
}
fmt.Println(slice)
}
}
gap /= 2
}
}
归并排序
总结来说就是将数组依次拆分,排序后再将数组合并,这里使用递归的办法。
package main
import "fmt"
// 合并并排序两个数组
func merge(s1 []int, s2 []int) []int {
// 获取两个需要合并数组的长度
s1_length, s2_length := len(s1), len(s2)
// 创建临时数组, 长度为需要合并的两个数组长度之和
var tmp_sice = make([]int, s1_length+s2_length)
// 在循环外部创建指针
var i, j int
// 比较两个数组,分别从0开始,将比较好后较小的值放入临时数组,当一个数组循环完毕时,推出循环
for i, j = 0, 0; i < s1_length && j < s2_length; {
if s1[i] <= s2[j] {
tmp_sice[i+j] = s1[i]
i++
} else {
tmp_sice[i+j] = s2[j]
j++
}
}
// 将剩余的数组元素追加到临时数组中
for ; i < s1_length; i++ {
tmp_sice[i+j] = s1[i]
}
for ; j < s2_length; j++ {
tmp_sice[i+j] = s2[j]
}
fmt.Println(tmp_sice)
// 直接将合并并排序好的临时数组返回
return tmp_sice
}
func merge_sort(slice []int) []int {
slice_length := len(slice)
// 当数组长度大于1时,进行排序,否则长度为1肯定为有序,为递归的退出条件
if slice_length > 1 {
var middle = slice_length / 2
// 递归,先将数组进行拆分, 再进行排序合并
return merge(merge_sort(slice[:middle]), merge_sort(slice[middle:]))
} else {
return slice
}
}
func main() {
slice := []int{7, 5, 8, 4, 3, 2, 6, 9, 1}
slice = merge_sort(slice)
fmt.Println(slice)
}
堆排序
参考https://www.cnblogs.com/chengxiao/p/6129630.html
数据结构
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
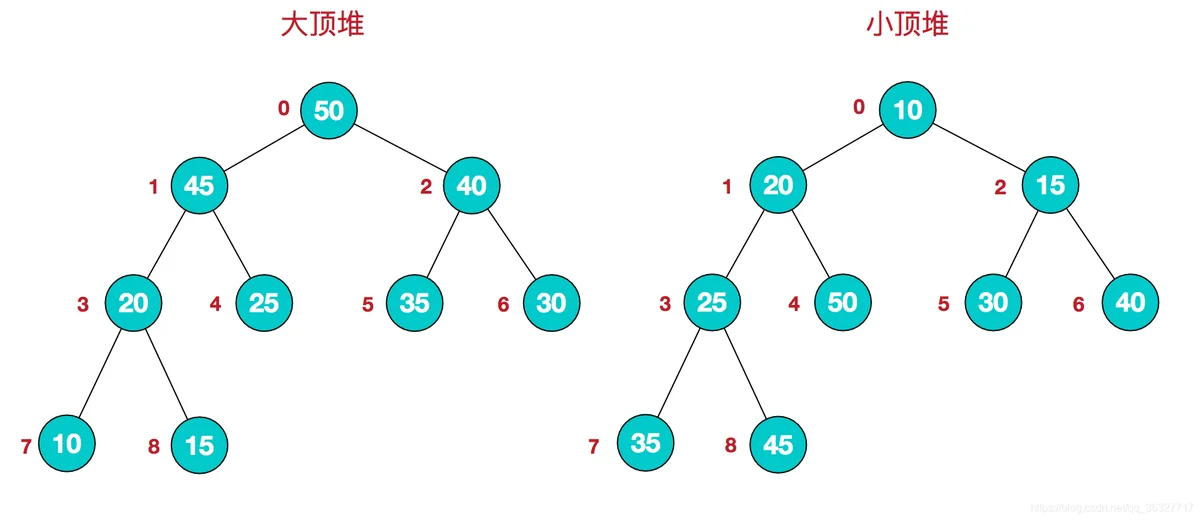
在数组中就如下图:

就能推导出以下规律:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
// study project main.go
package main
import "fmt"
func heap_sort(slice []int) []int {
var slice_length = len(slice)
Max_heap(slice, slice_length)
// 初始值为数组长度减去1表示最后一位不进行调整
for i := slice_length - 1; i >= 0; i-- {
// 第一次进入循环时,将最大数放到数组最后面
swap(slice, 0, i)
slice_length -= 1
heapify(slice, 0, slice_length)
}
return slice
}
// 从最后一个父子节点开始调正,循环过后堆顶得到的是最大的一个数
func Max_heap(slice []int, slice_length int) {
for i := slice_length / 2; i >= 0; i-- {
heapify(slice, i, slice_length)
}
}
// 调整堆
func heapify(slice []int, i, slice_length int) {
// 左子节点
left := 2*i + 1
// 右子节点
right := 2*i + 2
// i节点
largest := i
// 当左或者右子节点索引大于数组长度,不进行调整
// 当左或者右子节点大于其父节点时交换位置 大顶堆
if left < slice_length && slice[left] > slice[largest] {
largest = left
}
if right < slice_length && slice[right] > slice[largest] {
largest = right
}
if largest != i {
// 将父和子节点中最大的数向堆顶调整
swap(slice, i, largest)
// 调整子根, 此时largest指向的是交换后子节点的索引
heapify(slice, largest, slice_length)
fmt.Println(slice)
}
}
func swap(slice []int, i, j int) {
slice[i], slice[j] = slice[j], slice[i]
}
func main() {
slice := []int{4, 3, 6, 7, 5, 1, 9, 0, 2, 8}
slice = heap_sort(slice)
fmt.Println(slice)
}
快速排序
- 从数列中挑出一个元素,称为 “基准”(pivot)
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序
package main
import "fmt"
func quick_sort(slice []int, Left int, Right int) {
// 等价于当子数组长度为1
if Left >= Right {
return
}
left := Left
right := Right
// 取最左边为比较值
var pivot = slice[left]
// 退出条件为左索引等于右索引
for left < right {
// 当右索引的值大于比较值时,索引向左移动
for left < right && slice[right] >= pivot {
right -= 1
}
// 顺序结构,此时表示右索引的值比比较值小,所以将小的数放到左边
if left < right {
slice[left] = slice[right]
}
// 当左索引的值小于比较值时,索引向右移动
for left < right && slice[left] <= pivot {
left += 1
}
// 此时表示,左索引的值大于比较值,将大的数放到右边
if left < right {
slice[right] = slice[left]
}
// 左右索引重合时,将比较值放到此处
if left >= right {
slice[left] = pivot
}
}
// 将数组再分割成左右两组
// 左边部分递归
quick_sort(slice, Left, right-1)
// 右边部分递归
quick_sort(slice, right+1, Right)
}
func main() {
slice := []int{4, 3, 6, 7, 5, 1, 9, 0, 2, 8}
Left_index := 0
Right_index := len(slice)
quick_sort(slice, Left_index, Right_index-1)
fmt.Println(slice)
}
