百度百科:
1.冒泡排序(Bubble Sort),是一种计算机科学领域的较简单的排序算法。
2.它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果顺序(如从大到小、首字母从Z到A)错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换,也就是说该元素列已经排序完成。
3.这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名“冒泡排序”。
示意图:
菜鸟教程冒泡排序示意图:
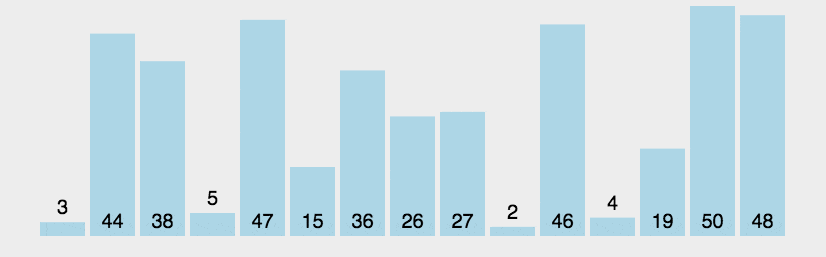
整体思路:
要从小到大排序
1.有n个数需要被排序;假设先选取第0个位置的数字和让其和后一位的数进行比较;
2.如果比较时发现当前数比后一个数大(即比较时,出现不符合我们规则的顺序),
交换两数;
3.然后选第1个位置的数字,继续遍历,一轮后,即可找出一个最大数;(即最后一位已经到达其应在位置;)
最后一个数已经不需要参与后面的比较了;
4.继续遍历,则每轮比较后,最后一个数就会到达其应到位置;
5.每轮能找出一个最大的数,则最多仅需n-1轮即可全部排序完成;因为其余数排序好后,最后一个数不用在找自己的位置了;(i表示外层for循环表示轮数)
6.每轮选中的数下标为j,从0开始;
因为选中的数和后一个比较,最后一个不用选中,所以j的上限 -1;
又因为每过1轮,最后一个数就会被定下来,所以每轮j的上限 -i;
2.1 基础冒泡排序
代码如下:
package main
import (
"fmt"
)
func main() {
//1.定义测试数组
// var intArr = [...]int {10,5,11,9,0} //test01
var intArr = [...]int {1,0,2,3} //test02
//2.输出排序前数组;
fmt.Println("排序前:",intArr)
/*整体思路:
3.从小到大排序
3.1有n个数需要被排序;假设先选取第0个位置的数字和让其和后一位的数进行比较;
3.2如果比较时发现当前数比后一个数大(即比较时,出现不符合我们规则的顺序),
交换两数;
3.3然后选第1个位置的数字,继续遍历,一轮后,即可找出一个最大数;(即最后一位已经到达其应在位置;)
最后一个数已经不需要参与后面的比较了;
3.4继续遍历,则每轮比较后,最后一个数就会到达其应到位置;
3.5每轮能找出一个最大的数,则最多仅需n-1轮即可全部排序完成;因为其余数排序好后,
最后一个数不用在找自己的位置了;(i表示外层for循环表示轮数)
3.6每轮选中的数下标为j,从0开始;
因为选中的数和后一个比较,最后一个不用选中,所以j的上限 -1;
又因为每过1轮,最后一个数就会被定下来,所以每轮j的上限 -i;
*/
for i:=0;i< len(intArr)-1;i++{
for j:=0;j< len(intArr)-1-i;j++{
if intArr[j+1] < intArr[j]{
temp := intArr[j+1]
intArr[j+1] = intArr[j]
intArr[j] =temp
}
}
fmt.Printf("第%v轮冒泡排序后:%v\n",i+1,intArr)
}
}
2.2 优化版冒泡排序
如果一轮遍历比较后,没有发生过交换,则当前每一个数都比他后面的数小;
即当前数组已有序;则立即可停止排序;
代码如下:
package main
import (
"fmt"
)
func main() {
//1.定义测试数组
var intArr = [...]int {10,5,11,9,0} //test01
// var intArr = [...]int {1,0,2,3} //test02
//2.输出排序前数组;
fmt.Println("排序前:",intArr)
/* 3.从小到大排序
3.1有n个数需要被排序;假设先选取第0个位置的数字和让其和后一位的数进行比较;
3.2如果比较时发现当前数比后一个数大(即比较时,出现不符合我们规则的顺序),
交换两数;
3.3然后选第1个位置的数字,继续遍历,一轮后,即可找出一个最大数;(即最后一位已经到达其应在位置;)
最后一个数已经不需要参与后面的比较了;
3.4继续遍历,则每轮比较后,最后一个数就会到达其应到位置;
3.5每轮能找出一个最大的数,则最多仅需n-1轮即可全部排序完成;因为其余数排序好后,
最后一个数不用在找自己的位置了;(i表示外层for循环表示轮数)
3.6每轮选中的数下标为j,从0开始;
因为选中的数和后一个比较,最后一个不用选中,所以j的上限 -1;
又因为每过1轮,最后一个数就会被定下来,所以每轮j的上限 -i;
*/
for i:=0;i< len(intArr)-1;i++{
//4.如果一轮遍历比较后,没有发生过交换,则当前每一个数都比他后面的数小,
//即当前数组已有序;则立即可停止排序;
//定义 is_changed ,记录每轮发生过交换;
var is_changed bool
for j:=0;j< len(intArr)-1-i;j++{
if intArr[j+1] < intArr[j]{
//如果顺序不对,则发生交换,字段变为 true;
is_changed = true
//交换两数位置;
intArr[j] = intArr[j+1] ^ intArr[j]
intArr[j+1] = intArr[j+1] ^ intArr[j]
intArr[j] = intArr[j+1] ^ intArr[j]
}
}
fmt.Printf("经过%v轮遍历;冒泡排序后结果为:%v\n",i+1,intArr)
//如果一整轮没交换过,则已经有序;退出排序;
if is_changed == false {
fmt.Printf("现在已经有序,直接停止;\n")
break;
}
}
}
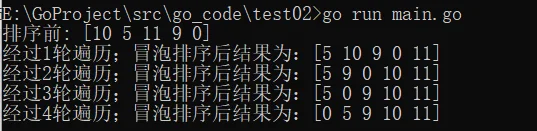
test01:
测试数据:{10,5,11,9,0}
测试结果:
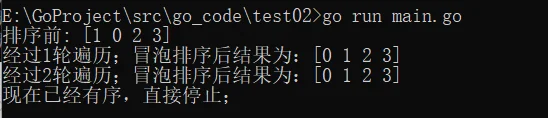
test02:
测试数据:{1,0,2,3}
测试结果: