7.1.1 椭圆曲线密码学概述
椭圆曲线密码学(Elliptic curve cryptography,缩写为 ECC),是基于椭圆曲线数学理论实现的一种非对称加密算法。
椭圆曲线算法又细分为多种具体的算法。Go语言内置的椭圆曲线是secp256R1算法,而比特币系统中使用secp256K1算法。以太坊系统虽然也采用secp256K1算法,但是跟比特币系统的secp256K1算法上又有所差异。
椭圆曲线公钥系统是代替RSA的强有力的竞争者,与经典的RSA、DSA等公钥密码***相比,椭圆密码***有明显的优势。
1、ECC与RSA算法的优势对比
(1)安全性能更高(ECC可以使用更短的**),同等安全强度下,两者秘钥长度的对比如下表所示。

(2)处理速度快,计算量小,处理速度快 在私钥的处理速度上(解密和签名),ECC远 比RSA、DSA快得多。
(3)存储空间占用小,ECC的**尺寸和系统参数与RSA、DSA相比要小得多, 所以占用的存储空间小得多。
(4)带宽要求低使得ECC具有广泛的应用前景。
ECC的这些特点使它必将取代RSA,成为通用的公钥加密算法。
7.1.2 数字签名的概念
所谓数字签名(Digital Signature)(又称公开**数字签名、电子签章)是一种类似写在纸上的普通的物理签名,但是使用了公钥加密领域的技术实现,用于鉴别数字信息的方法。一套数字签名通常定义两种互补的运算,一个用于签名,另一个用于验证。数字签名可以验证数据的来源,可以验证数据传输过程中是否被修改。
数字签名是通过非对称加密算法中的私钥加密、公钥解密过程来实现的。私钥加密就是私钥签名,公钥解密就是公钥验证签名。因此数字签名由两部分组成:第一部分是使用私钥为消息创建签名的算法,第二部分是允许任何人用公钥来验证签名的算法。数字签名的使用流程如图13.12所示。
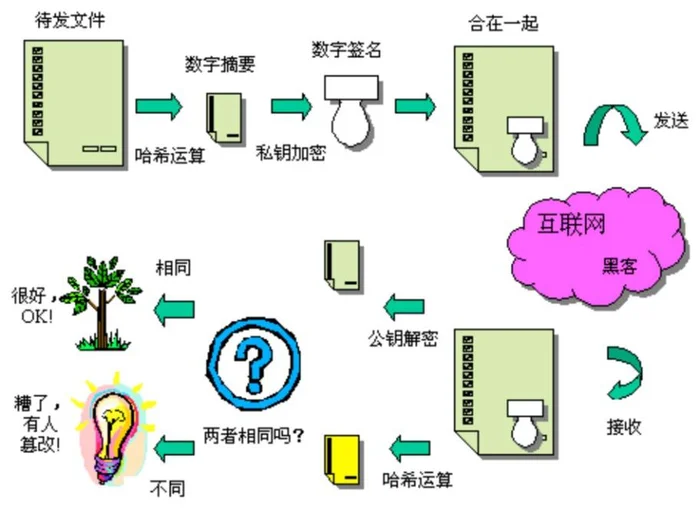
图7.1 数字签名
数字签名应该满足如下要求。
l 签名不可伪造性;
l 签名不可抵赖的;
l 签名可信性,签名的识别和应用相对容易,任何人都可以验证签名的有效性;
l 签名是不可复制的,签名与原文是不可分割的整体;
l 签名消息不可篡改,因为任意比特数据被篡改,其签名便被随之改变,那么任何人可以验证而拒绝接受此签名。
