lingo中的集合用法很多,这里主要通过几个例题来进行讲解
对于每一个问题,都要先找到对应的目标函数,然后对相应值进行初始化,然后找到约束条件等进行求解
例1:SAILCO公司需要决定下四个季度的帆船生产量。下四个季度的帆船需求量分别是40条,60条,75条,25条,这些需求必须按时满足。每个季度正常的生产能力是40条帆船,每条船的生产费用为400美元。如果加班生产,每条船的生产费用为450美元。每个季度末,每条船的库存费用为20美元。假定生产提前期为0,初始库存为10条船。如何安排生产可使总费用最小?
分析:用DEM,RP,OP,INV分别表示需求量、正常生产的产量、加班生产的产量、库存量,则DEM,RP,OP,INV对每个季度都应该有一个对应的值,也就说他们都应该是一个由4个元素组成的数组,其中DEM是已知的,而RP,OP,INV是未知数。

MODEL: !模型开始;
SETS: !集合定义开始;
QUARTERS/1,2,3,4/:DEM,RP,OP,INV;
!集合QUARTERS类似于数组,DEM等表示该集合包含的元素,这里一共有四个元素。/1,2,3,4/表示该集合的大小,对应着实际问题的每一个季度
/1,2,3,4/等价于/1..4/,当集合大小比较大时,建议写后者;
ENDSETS !集合定义结束;
MIN=@SUM(QUARTERS:400*RP+450*OP+20*INV);
!@sum(),求和函数,表示对该集合所有依次进行求和,由于这里是对所有,所以省去了循环变量,
这里等价于@SUM(QUARTERS(i): 400*RP(i) +450*OP(i) +20*INV(i) );
@FOR(QUARTERS(I):RP(I)<40);
!@for类似于c/c++中的for循环,对其中操作循环进行;
@FOR(QUARTERS(I)|I#GT#1: !|表示对于循环的限制,#GT#表示大于,这里具体含义:I大于1时即执行循环,否则不执行;
INV(I)=INV(I-1)+RP(I)+OP(I)-DEM(I););
INV(1)=10+RP(1)+OP(1)-DEM(1); !对应着第一季度的条件
DATA: !初始数据段开始
DEM=40,60,75,25;
ENDDATA !初始数据段结束;
END !模型结束;
接下里这里例子会讲到关于集合的派生问题,这个跟c++里面的继承与派生比较相像
例2:建筑工地的位置(用平面坐标a,b表示,距离单位:公里)及水泥日用量d(吨)下表给出。有两个临时料场位于P (5,1), Q (2, 7),日储量各有20吨。从A, B两料场分别向各工地运送多少吨水泥,使总的吨公里数最小。两个新的料场应建在何处,节省的吨公里数有多大?


MODEL:
Title Location Problem;
sets:
demand/1..6/:a,b,d; !该集合对应着建筑工地,每一个建筑工地有两个坐标还有一个需求量,所以元素有三个;
supply/1..2/:x,y,e; !该集合对应着料场,元素是坐标与储存量;
link(demand,supply):c; !由上面的demand supply派生而成,可以认为现在link是一个6行(demand)2列(supply)的矩阵,
矩阵中元素的值代表着每一个建筑工地接受各个料场的具体水泥量;
endsets
data:
!locations for the demand(需求点的位置);
a=1.25,8.75,0.5,5.75,3,7.25;
b=1.25,0.75,4.75,5,6.5,7.75;
!quantities of the demand and supply(供需量);
d=3,5,4,7,6,11; e=20,20;
enddata
init:
!initial locations for the supply(初始点);
x,y=5,1,2,7;
endinit
!Objective function(目标);
min=@sum(link(i,j): c(i,j)*((x(j)-a(i))^2+(y(j)-b(i))^2)^(1/2) ); !表示对link中所有元素即六行二列都进行此求和操作;
!demand constraints(需求约束);
@for(demand(i):@sum(supply(j):c(i,j)) =d(i);); !@sum里面表示对j进行循环用supply,@for表示对i进行循环用demand(i),
这里表示对所有的建筑工地,工地对应的的需求量等于各个草料场供给量的和;
!supply constraints(供应约束);
@for(supply(i):@sum(demand(j):c(j,i)) <=e(i); );
@for(supply: @bnd(0.5,X,8.75); @bnd(0.75,Y,7.75); ); !表示x, y的范围,@bnd(a, x, b): a <= x <= b;
END
例3: (最短路问题) 在纵横交错的公路网中,货车司机希望找到一条从一个城市到另一个城市的最短路.下图表示的是公路网,节点表示货车可以停靠的城市,弧上的权表示两个城市之间的距离(百公里).那么,货车从城市S出发到达城市T,如何选择行驶路线,使所经过的路程最短?

分析:
假设从S到T的最优行驶路线P 经过城市C1, 则P中从S到C1的子路也一定是从S到C1的最优行驶路线;假设 P 经过城市C2, 则P中从S到C2的子路也一定是从S到C2的最优行驶路线.因此, 为得到从S到T的最优行驶路线, 只需要先求出从S到Ck(k=1,2)的最优行驶路线,就可以方便地得到从S到T的最优行驶路线. 同样,为了求出从S到Ck(k=1,2)的最优行驶路线, 只需要先求出从S到Bj(j=1,2)的最优行驶路线;为了求出从S到Bj(j=1,2)的最优行驶路线, 只需要先求出从S到Ai(i=1,2,3)的最优行驶路线. 而S到Ai(i=1,2,3)的最优行驶路线是很容易得到的(实际上, 此例中S到Ai(i=1,2,3)只有唯一的道路) .
此例中可把从S到T的行驶过程分成4个阶段,即S→Ai(i=1,2或3),Ai→Bj(j=1或2),Bj→Ck(k=1或2),Ck→ T. 记d(Y,X)为城市Y与城市X之间的直接距离(若这两个城市之间没有道路直接相连,则可以认为直接距离为∞),用L(X)表示城市S到城市X的最优行驶路线的路长:

model:
SETS:
CITIES /S,A1,A2,A3,B1,B2,C1,C2,T/: L; !属性L(i)表示城市S到城市i的最优行驶路线的路长;
ROADS(CITIES, CITIES)/ !派生集合ROADS表示的是网络中的道路(弧);
S,A1 S,A2 S,A3 !由于并非所有城市间都有道路直接连接,所以将弧具体列出,如果这里不是具体给出则会默认所有城市都有边相连;
A1,B1 A1,B2 A2,B1 A2,B2 A3,B1 A3,B2
B1,C1 B1,C2 B2,C1 B2,C2
C1,T C2,T/: D; !属性D( i, j) 是城市i到j的直接距离(已知);
ENDSETS
DATA:
D = 6 3 3
6 5 8 6 7 4
6 7 8 9
5 6;
L= 0, , , , , , , , ; !因为L(S)=0,这里的,不能省略,表示虽然对应值还未确定,但是必须为他们预留位置,不然会出错;
ENDDATA
@FOR( CITIES( i)|i#GT#@index(S): !这行中“@index(S):表示S在CITIES中的下标”可以直接写成“1”;
L(i) = @MIN( ROADS(j, i): L( j) + D( j, i)); ); !这就是前面写出的最短路关系式,ROAD(j, i)表示对所以从j到i的边循环一遍;
end
例4:篮球队需要选择5名队员组成出场阵容参加比赛.8名队员的身高及擅长位置见下表:
| 队员 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 身高(m) | 1.92 | 1.90 | 1.88 | 1.86 | 1.85 | 1.83 | 1.80 | 1.78 |
| 擅长位置 | 中锋 | 中锋 | 前锋 | 前锋 | 前锋 | 后卫 | 后卫 | 后卫 |
出场阵容应满足以下条件:
(1)只能有一名中锋上场;
(2)至少有一名后卫;
(3)如1号和4号均上场,则6号不出场;
(4)2号和8号至少有一个不出场.
问应当选择哪5名队员上场,才能使出场队员平均身高最高?
分析:典型0/1问题,这个时候是一维的情况,可以设置一个一维的集合,取值只能是0或者1,为1时代表选取对应运动员,否则不选
目标函数:该集合与对应身高相乘求和,即为1时表示选取侧求和相加,为0时侧不选取,不做任何处理
限制条件:必须选取五名,其他条件题目中应该满足的条件已经给的比较清楚了,具体见下面代码
model:
!集合段;
sets:
player/1..8/:high, match;
endsets
!目标与约束段;
max = @sum(player: high * match) / 5;
@for(player: @bin(match)); !限制match必须值必须为0或者1,@bin(x):x为0或1;
@sum(player: match) = 5; !必须选取五名;
match(1) + match(2) = 1; !只能有一名中锋上场;
match(6) + match(7) + match(8) >= 1; !至少有一 名后卫;
match(1) + match(4) + match(6) <= 2; !如1号和4号均上场,则6号不出场;
match(2) + match(8) >= 1; !2号和8号至少有一个不出场;
!数据段;
data:
high = 1.92 1.90 1.88 1.86 1.85 1.83 1.80 1.78;
enddata
end
显示结果中的match
MATCH( 1) 0.000000 -0.3840000
MATCH( 2) 1.000000 -0.3800000
MATCH( 3) 1.000000 -0.3760000
MATCH( 4) 1.000000 -0.3720000
MATCH( 5) 1.000000 -0.3700000
MATCH( 6) 1.000000 -0.3660000
MATCH( 7) 0.000000 -0.3600000
MATCH( 8) 0.000000 -0.3560000
有时候会觉得match过多难以找到被选中的即match为1的具体哪些值,这个时候可以lingo -->solution
然后match显示如下
Variable Value Reduced Cost
MATCH( 2) 1.000000 -0.3800000
MATCH( 3) 1.000000 -0.3760000
MATCH( 4) 1.000000 -0.3720000
MATCH( 5) 1.000000 -0.3700000
MATCH( 6) 1.000000 -0.3660000
例5: 某商业公司计划开办5家新商店.为了尽早建成营业,商业公司决定由5家建筑公司分别承建.已知建筑公司Ai(i=1,2,3,4,5)对新商店Bj(j=1,2,3,4,5)的建造费用的报价(万元)为cij(i,j=1,2,3,4,5),见下表.商业公司应当对5家建筑公司怎样分配建造任务,才能使总的建造费用最少?
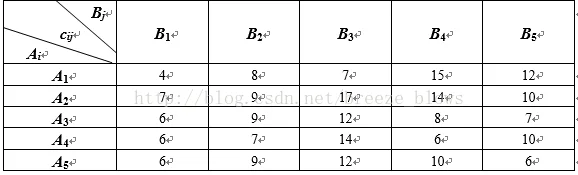
分析:典型的01问题,设置一个五行(对应集合中的建筑公司) 五列(对应着集合中的建筑物) 的矩阵,当其中元素为1时表示该建筑公司建筑该建筑物,为0时侧相反。
目标函数:该矩阵对应的值与题目中的价格矩阵一一对应相乘然后求和,即该矩阵为1时侧表示某建筑公司建筑对应建筑物侧求和加上,否则侧不加
很明显约束条件便是一个建筑公司只能建筑一个建筑物,即矩阵每一列的和只能为一; 一个建筑物只能被一个建筑公司建成,即每一列的和只能为一;而且不同建筑公司必须建筑不同的建筑物;对应设置的矩阵其中元素必须为0、1值
model:
!集合段;
sets:
company/1..5/;
building/1..5/; !这里的集合可以没有元素,仅仅为了派生;
pairs(company, building):price, match;
endsets
!目标与约束段;
min=@sum(pairs(i,j):price(i,j)*match(i,j));
@for(pairs(i,j):@bin(match(i,j))); !限制match必须为0或1 @bin(x):x为0或1;
@for(company(i):@sum(building(j): match(j, i)) = 1); !限制每一个建筑公司只能建筑一个建筑物;
@for(building(i):@sum(company(j): match(i, j)) = 1); !限制每一个建筑物只能被一家建筑公司建成;
!数据段;
data:
price = 4 8 7 15 12
7 9 17 14 10
6 9 12 8 7
6 7 14 6 10
6 9 12 10 6;
enddata
end
