三、算法流程与代码实现

一、算法介绍

  决策树(Decision Tree）是在已知各种情况发生概率的基础上，通过构成决策树来求取净现值的期望值大于等于零的概率，评价项目风险，判断其可行性的决策分析方法，是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干，故称决策树。
  在机器学习中，决策树是一种预测分类模型，并广泛用在各种预测分类场景中，是一种十分常用的分类方法。决策树是一种监督学习，可以通过不同的算法来计算信息增益，并以此为依据来创建决策树。

二、数据集信息

  在本次博客中，我们使用泰坦尼克号数据集来进行决策树模型的训练和评估。
  该数据集主要包含以下信息：

属性名称	描述
PassengerId	乘客id
Survived	是否幸存
Pclass	船票等级
Name	乘客姓名
Sex	乘客性别
Age	乘客年龄
SibSp	非直系亲缘数量
Parch	直系亲缘数量
Ticket	船票号码
Fare	船票价格
Cabin	船舱
Embarked	登陆港口

  共有891条记录。

三、算法流程与代码实现

1、加载数据集以及特征值的选取

  通过实现函数loadDataSet() 来进行数据集的加载。

func loadDataSet(trainScale int) ([][]string, [][]string, []string) {

	file, err := os.Open("titanic.csv")
	if err != nil {
		fmt.Println("Error:", err)
		return nil, nil, nil
	}

	defer func(file *os.File) {
		err := file.Close()
		if err != nil {

		}
	}(file)

	reader := csv.NewReader(file)

	var features []string
	var trainDataSet [][]string
	var testDataSet [][]string

	temp, _ := reader.Read()
	
    /** 读取特征 **/

	curr := 0

	for {
		record, err := reader.Read()

		if err == io.EOF {
			break
		} else if err != nil {
			fmt.Println("Error:", err)
			return nil, nil, nil
		}

		var tempRecord []string

		/** 读取训练集和测试集，并对数据进行裁剪和清洗 **/

		curr++
	}

	return trainDataSet, testDataSet, features
}

  然后我们对数据集进行裁剪和清洗。在特征值的分析中，我们可以发现乘客id（PassengerId）、乘客姓名（Name）、船票号码（Ticket）、非直系亲缘数量（SibSp）与直系亲缘数量（Parch）与乘客是否幸存没有直接关系，可以先暂时忽视；而船票价格（Fare）与船票等级（Pclass）有直接关系，所以我们可以只保留更加集中的船票等级；而船舱（Carbin）的样本缺失率在70%以上，无法进行补齐，所以丢弃；登录港口（Embarked）有少量的缺失值，通过分析我们发现，登陆港口为S的记录占总记录的70%以上，所以将缺失值补为S。
  最终，选取船票等级（Pclass）、乘客性别（Sex）和登录港口（Embarked）作为训练特征集，选取是否幸存（Survived）作为标签。

2、信息熵和信息增益的计算

  ID3算法通过计算信息增益来确定下一个节点的特征。而信息增益需要通过信息熵来确定。

$Ent(t) = -$$\sum_{i=0}^n$$p(i$$\mid$$t)log_2$$p(i$$\mid$$t)$

  实现代码如下：

func calcEnt(data [][]string) float64 {
   // 数据行数
   num := len(data)
   // 记录标签出现的次数
   labelMap := make(map[string]int)
   for _, temp := range data {
   	curLabel := temp[len(temp)-1]
   	if _, ok := labelMap[curLabel]; !ok {
   		labelMap[curLabel] = 0
   	}
   	labelMap[curLabel]++
   }

   ent := 0.0

   // 计算经验熵
   for _, v := range labelMap {
   	prob := float64(v) / float64(num)
   	ent -= math.Log2(prob) * prob
   }

   return ent
}

  之后计算信息增益，计算信息增益的过程便是选择最佳特征的过程。信息增益是父亲节点的信息熵减去所有子节点的信息熵。

$Gain(D,a) = Ent(D)-$${\mid D_i \mid \over \mid D \mid}$$\sum_{i=0}^n$$Ent(D_i)$

func chooseBestFeature(dataSet [][]string) int {
   // 特征数量
   featureNum := len(dataSet[0]) - 1
   // 计算数据集的熵
   baseEntropy := calcEnt(dataSet)
   // 信息增益
   bestInfoGain := 0.0
   // 最优特征的索引值
   bestFeatureIdx := -1
   // 遍历所有特征
   for i := 0; i < featureNum; i++ {
   	// 获取某一列的所有特征值
   	var featList []string
   	for _, temp := range dataSet {
   		featList = append(featList, temp[i])
   	}
   	// 获取不同的特征值
   	uniqueFeatureValues := distinct(featList)
   	// 经验条件熵
   	newEntropy := 0.0
   	// 计算信息增益
   	for _, temp := range uniqueFeatureValues {
   		// 划分子集
   		subDataSet := splitDataSet(dataSet, i, temp.(string))
   		// 计算子集的概率
   		prob := float64(len(subDataSet)) / float64(len(dataSet))
   		// 计算经验条件熵
   		newEntropy += prob * calcEnt(subDataSet)
   	}
   	// 信息增益
   	infoGain := baseEntropy - newEntropy
   	// 计算信息增益
   	if infoGain > bestInfoGain {
   		// 更新信息增益，找到最大的信息增益
   		bestInfoGain = infoGain
   		// 记录信息增益最大的特征的索引
   		bestFeatureIdx = i
   	}
   }

   return bestFeatureIdx
}

  通过信息熵和信息增益的计算，我们便可获取最优的节点划分特征，也便可以基于此构造决策树。

3、决策树的构建

  我们可以通过递归的方式构建决策树。代码如下：

func createTree(dataSet [][]string, labels []string, remainFeatures []string) map[string]interface{} {
	// 获取分类标签
	var classList []string
	for _, temp := range dataSet {
		classList = append(classList, temp[len(temp)-1])
	}
	// 如果类别相同，就停止划分
	if len(classList) == count(classList, classList[0]) {
		return map[string]interface{}{classList[0]: nil}
	}
	// 返回出现次数最多的类标签
	if len(dataSet[0]) == 1 {
		return map[string]interface{}{vote(classList): nil}
	}
	// 选择最优特征
	bestFeatIdx := chooseBestFeature(dataSet)
	// 获取最优特征的标签
	bestFeatLabel := labels[bestFeatIdx]
	remainFeatures = append(remainFeatures, bestFeatLabel)
	// 根据最优特征的标签生成树
	tree := make(map[string]interface{})
	// 删除已经使用的特征标签
	tar := make([]string, len(labels))
	copy(tar, labels)
	labels = append(tar[:bestFeatIdx], tar[bestFeatIdx+1:]...)
	// 获取最优特征中的属性值
	var featValues []string
	for _, temp := range dataSet {
		featValues = append(featValues, temp[bestFeatIdx])
	}
	// 去掉重复的属性值
	uniqueValues := distinct(featValues)
	// 遍历特征创建决策树
	for _, temp := range uniqueValues {
		if _, ok := tree[bestFeatLabel]; !ok {
			tree[bestFeatLabel] = make(map[string]interface{})
		}
		tree[bestFeatLabel].(map[string]interface{})[temp.(string)] = createTree(splitDataSet(dataSet, bestFeatIdx, temp.(string)), labels, remainFeatures)
	}

	return tree
}

  使用map作为决策树的数据结构，以特征为key，以子树（map）为value，便可构建出完整的决策树，格式如下：

map[性别]:map[0:map[体重:map[0:map[no:<nil>] 1:map[yes:<nil>]]] 1:map[yes:<nil>]]]

4、分类

  分类时，我们只需要从根节点开始，依次通过比对特征值到达叶子节点即可。

func classify(tree map[string]interface{}, features []string, testVec []string) string {
	// 获取决策树根节点
	var firstStr string
	for k, v := range tree {
		if v == nil {
			return k
		}

		firstStr = k
	}
	root := tree[firstStr].(map[string]interface{})

	featIdx := index(features, firstStr)

	var classLabel string

	for k, v := range root {
		if strings.Compare(testVec[featIdx], k) == 0 {
			if v == nil {
				classLabel = k
			} else {
				classLabel = classify(root[k].(map[string]interface{}), features, testVec)
			}
		}
	}

	return classLabel
}

四、模型的训练与测试

  运行函数代码样例如下：

func main() {
	trainDataSet, testDataSet, features := loadDataSet(810)

	var remainLabels []string

	tree := createTree(trainDataSet, features, remainLabels)

	fmt.Println(tree)

	total := 0

	correctNum := 0

	for _, temp := range testDataSet {
		result := classify(tree, features, temp[:len(temp)-1])
		if strings.Compare(result, temp[len(temp)-1]) == 0 {
			correctNum++
		}

		total++
	}

	rate := float64(correctNum) / float64(total) * 100

	fmt.Println("测试集正确率：" + fmt.Sprintf("%.2f", rate) + "%")

}

  程序运行截图如下：

  由于决策树的准确率主要由决策树的规模和训练集的规模来决定，所以这里通过不同的特征集和训练集的占比来对模型性能进行评估。
  通过实验，得到以下结果：

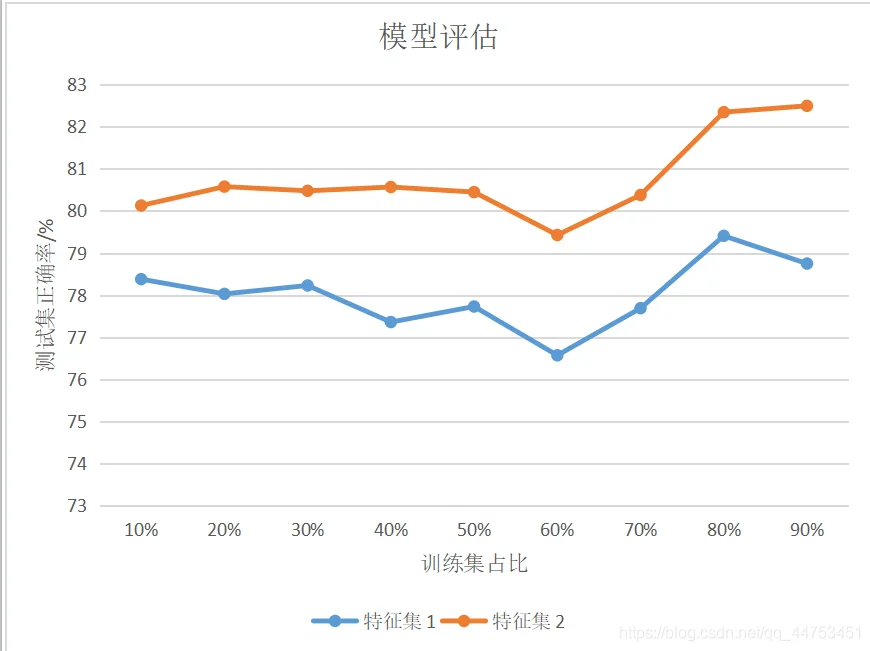
  其中，特征集1包含特征：性别、登录港口；特征集2包含特征：性别、船票等级和登陆港口。每组实验运行10次，取平均值。

五、结果分析

  通过分析实验结果，我们可以发现相同特征集的情况下，训练集权重的大小对模型的预测准确率影响不大，会有所波动，但大体趋势是增长的，会在训练集占比60%时有一个较大的波动；在训练集占比相同的情况下，低相关特征越多，模型的预测准确率也会越准确。

<script type="text/javascript" src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML"></script> <script type="text/x-mathjax-config"> MathJax.Hub.Config({ tex2jax: {inlineMath: [['$', '$']]}, messageStyle: "none" }); </script>