大家好,今天,我们来介绍一下决策树的原理。
决策树算法在当今机器学习中经常用到,它既可以作为分类算法,也可以作为回归算法,下面我会和大家对这个算法中的一些理论进行一一介绍。
决策树算法通俗来讲,就是一种按照重要性(信息增益)层层分类的分类方法,此文章借西瓜书中的例子来为大家讲解
信息增益:“信息熵”是度量样本集合纯度最常用的一种指标,假设当前样本集合D中第k类样本所占的比例为pk(k=1,2,3,...,|y|),则D的信息熵定义为 :
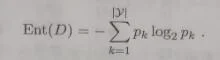
Ent(D)的值越小(也就是树的结构越简单),则D的纯度越高
假定离散属性a有V个可能的取值{a1,a2,a3,…,aV},若使用a来对样本集D进行划分,则会产生V个分支结点,其中第v个分支结点包含了D中所有在属性a上取值为av的样本,记为Dv。我们可根据信息熵的式子计算出Dv的信息熵,再考虑到不同的分支结点所包含的样本数不同,给分支结点赋予权重|Dv|/|D|,即样本数越多的分支结点的影响越大,于是可计算出用属性a对样本集D进行划分所获得的“信息增益” :
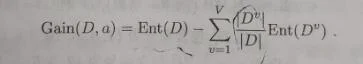
下面我们来看一组现实中的数据:
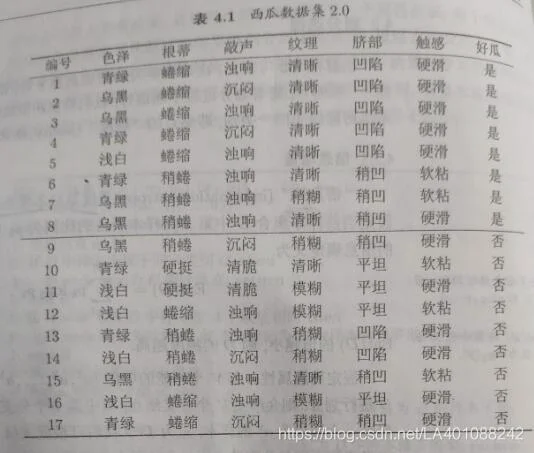
上图为判别西瓜好坏的一组数据集,该数据集包含17个训练样例,显然|y|=2,正例占p1=8/17,反例占p2=9/17。于是可计算出根结点的信息熵为:
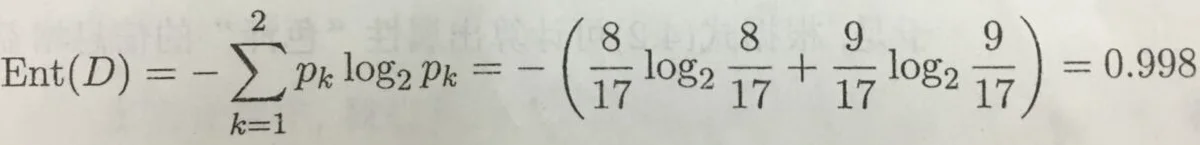
然后,我们要计算出当前属性集合{色泽,根蒂,敲声,纹理,脐部,触感}中每个属性的信息增益。以属性“色泽”为例,它有3个可能的取值。若使用该属性对D进行划分,则可得到3个子集,分别记为D1(色泽=青绿),D2(色泽=乌黑),D3(色泽=浅白)。则这3个特征对应的信息熵为:
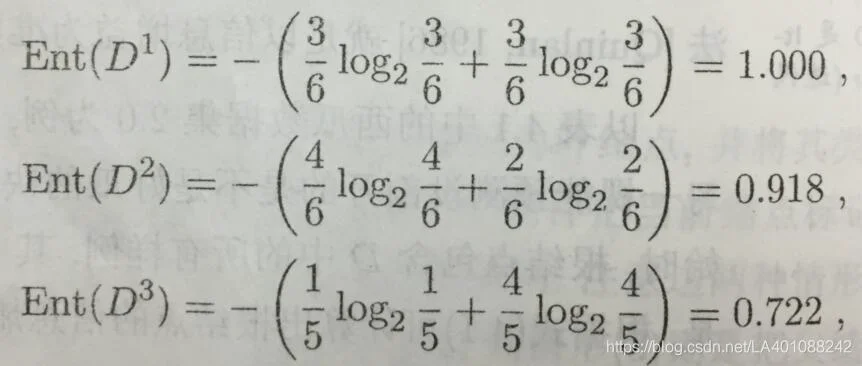
于是可计算出属性“色泽“的信息增益为:
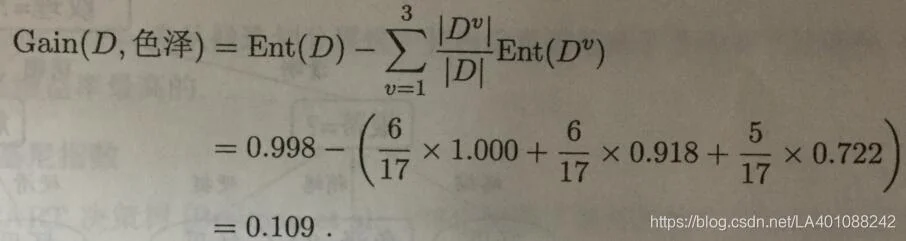
同理,我们可计算出其他属性的信息增益:

由此图可知,相对于其他特征,“纹理”的信息增益最大,于是它被选为划分属性。
信息增益比:实际上,信息增益准则对可取数值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响,著名的C4.5决策树算法不直接使用信息增益,而是使用“增益率”来选择最优划分属性,增益率的定义公式为:
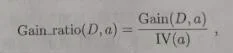
其中:
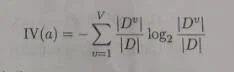
称为属性a的“固有值”,属性a的可能取值数目越多(即V越大),则IV(a)的值通常会越大,例如,对上面西瓜数据集,有IV(触感)=0.874(V=2),IV(色泽)=1.580(V=3),IV(编号)=4.088(V=17)。
注:V实际上就是每列特征的种类数
“基尼系数”(Gini index):CART决策树使用Gini系数来选择划分属性数据集D的纯度可以用基尼值来度量:
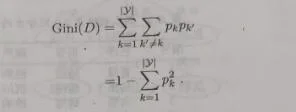
直观来说,Gini(D)反应了从数据集D中随机抽取两个样本,其类别标记不一致的概率,因此,Gini(D)越小,则表示数据集D的纯度越高。
属性a的基尼指数定义为:
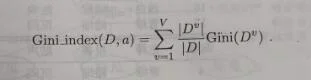
于是,我们在候选属性集合A中,选择那个使得划分后基尼指数最小的属性作为最优属性划分,即a*=arg min Gini_index(D,a)(a∈A)。
注:此文章参照《机器学习》------------周志华一书 编写,希望可以帮到大家。
