决策树作为最基础、最常见的 有监督学习模型,常用来做语分类问题、回归问题
决策树算法3要素: 特征选择、决策树生成、决策树剪枝
决策树生成的过程是使用满足划分标准的特征不断地将数据集划分为具有更高纯度和更少不确定性的子集的过程。
[En]
The process of decision tree generation is the process of constantly dividing a data set into a subset with higher purity and less uncertainty using features that meet the partition criteria.
对于当前数据集D的每一次划分,都希望根据某特种划分之后的各个子集的纯度更高,不确定性更小
如何度量划分数据集前后的数据集的纯度以及不确定性呢?
答案:特征选择准则
常见的决策树算法:ID3、C4.5、CART
特征选择准则:
目的:使用某特种对数据集划分之后,各数据子集的纯度要比划分前的数据集D的纯度高(不确定性要比划分前数据集D的不确定性低)
注意:
- 划分后的纯度为各数据子集的纯度加和(子集占比*子集的经验熵)
- 度量划分前后的纯度变化,用子集的纯度之和与划分前的数据集D的纯度进行对比
特征选择的标准是衡量样本集的不确定性和纯度的方法。本质是一样的,但定义是不同的。
[En]
The criterion of feature selection is the method to measure the uncertainty and purity of the sample set. The essence is the same, but the definition is different.
熵:度量随机变量的不确定性(纯度)
定义:假设随机变量X的可能取值有x1、x2、。。。xn
对于每一个可能的取值xi,其概率P(X=xi)=pi,(i=1,2,3…,n)
因此随机变量X的熵:
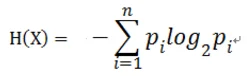
对于样本集合D来说,随机变量X是样本类别,即,假设样本有K各类别,每个类别的概率是:
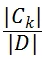
其中:|Ck|表示类别k的样本个数,|D)表示样本总数
则对于样本集合D来说熵(经验熵)为:
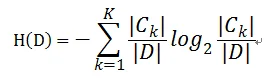
1、常见的决策树算法1:信息增益(ID3算法)
定义:以某特征划分数据集前后的熵的差值
在熵的理解那部分提到了,熵可以表示样本集合的不确定性,熵越大,样本的不确定性就越大。因此可以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合D划分效果的好坏
划分前样本集合D熵是一定的,entroy(前)
使用某个特征A划分数据集D,计算划分后的数据子集的熵entroy(后)
信息增益=entroy(前)-entroy(后)
公式:
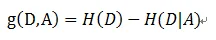
计算使用所有特征划分数据集D,得到多个特征划分数据集D的信息增益,从这些信息增益中选择最大的,因而当前节点的划分特征便是使信息增益最大的划分所使用的特征
信息增益的理解:
对于待划分的数据集D,其entroy(前)是一定的,但是划分之后的熵entroy(后)是不定的,entroy(后)越小说明使用此特征划分得到的子集的不确定性越小(也就是纯度越高),因此entroy(前)-entroy(后)差异越大,说明使用当前特征划分数据集D的话,其纯度上升的更快。而我们在构建最优的决策树的时候总希望能够快速到达纯度跟高的集合,这一点可以参考优化算法中的梯度下降算法,每一步沿着负梯度方法最小化损失函数的原因就是负梯度方向是函数值见效最快的方向。同理:在决策树构建的过程中,我们总希望集合往最快到达纯度更高的子集合方向发展,因此我们总是选择使得信息增益最大的特征来划分当前数据集D。
缺点:信息增益偏向取之较多的特征
原因:当特征的取值较多时,根据此特征划分最容易得到纯度最高的子集,因此划分之后的熵最低,由于划分前的熵是一定的,因此信息增益更大,因此信息增益比较偏向取之较多的特征
2、常见的决策树算法:最大信息增益比(C4.5算法)
—待续
Original: https://blog.csdn.net/wwxsoft/article/details/125613839
Author: dudu妈
Title: 决策树介绍及常用算法
