本文是《机器学习宝典》第 15 篇，读完本文你能够掌握机器学习中决策树如何解决回归问题。话说回归决策树可是面试常考的一类题目，所以你懂得????。
在 决策树进阶 中我们学习到了决策树的剪枝处理，对连续特征以及缺失值的处理。这篇文章来介绍下决策树在解决回归问题中的应用。前面我们知道 CART 能够解决分类问题，实际上它也是可以解决回归问题的。下图是只使用一个特征的情况下 与回归决策树的拟合的示意图。
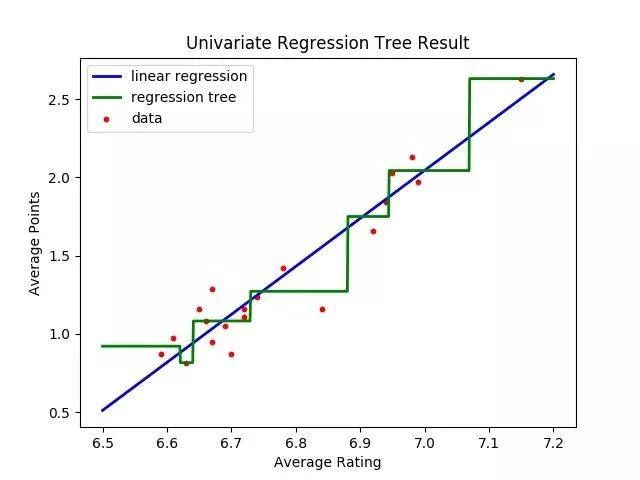
可以看到，相比于 对数据的拟合比较平滑，回归决策树的拟合就没有那么平滑了。接下来看下回归决策树的一些理论知识。
回归树结点划分简介
在前面的 学习中，我们已经知道：在使用决策树解决分类问题时，叶子结点的输出是按照多数投票原则决定最终的类别，即该结点下包含样本数最多的类别。在使用决策树进行回归预测时，叶子结点的输出是该结点下所有样本的目标值的均值。
假设包含了 m 个样本的数据集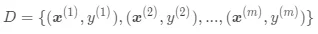 
，每个样本都包含了 n 个特征 。
回归树在第一次构建时，每次遍历已有的特征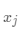 
，并对该特征选择一个切分点 s，这样能够将数据集划分为两个结点：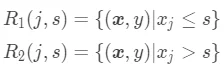
这两个结点对应了特征满足特定条件下的输出值（如果该结点最终是叶子结点，则输出值也就是预测值）：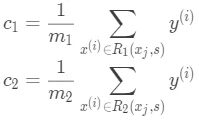
其中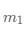 
表示 
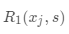中包含的样本数， 
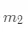表示 
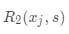中包含的样本数。直观的理解就是，当样本属于 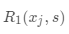结点，即 
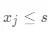时，模型预测的结果为 c1；当样本属于 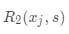结点，即 
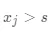时，模型预测的结果为 c2 。
回归树的结点划分依据
对回归树的区域结点有了解了之后，自然而然就会想到每次划分时的依据。回归树每个结点在划分时的依据不再是最小基尼系数，而是最小平方误差。平方误差定义如下：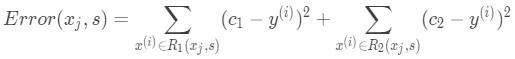
有了误差函数之后，我们每次结点划分时，选择能够使得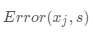 
最小的特征 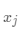以及切分点 s 来进行。
回归树算法流程
通过前面的介绍，我们已经知道回归树能够划分生成结点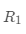 
和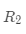 
，我们可以设置停止条件（比如树深、叶子结点包含的最少样本数）来控制决策树是否继续生长。如果停止生长，则对应的结点变为叶子结点，否则就是内部结点。由于模型结果最终由叶子结点给出，假设最后总共生成了 L 个叶子结点，分别用 
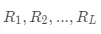表示，对于内部结点我们则不关心它的表示方式。
现在来看下最终回归树的算法流程。
（1）遍历所有特征，找到最优划分特征为 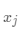和切分点 
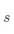，满足 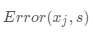最小，然后划分为两个结点。
（2）对生成的两个结点重复调用步骤（1），直至满足停止条件。
（3）根据最终生成的所有的 L 个叶子结点，得到回归树：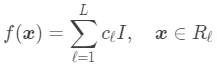
其中，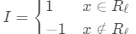
。
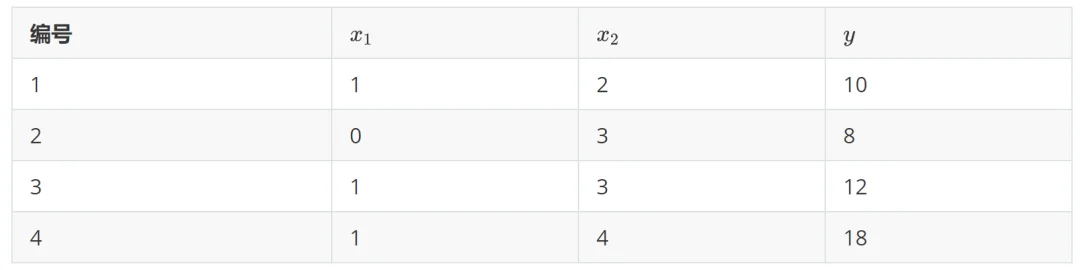
示例演示
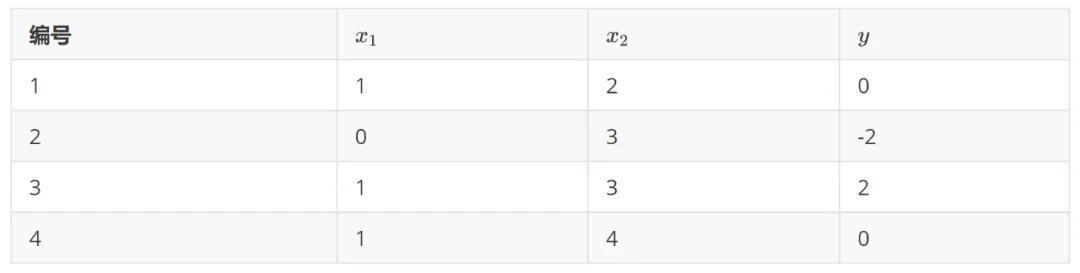
下面是一个示例训练集，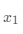
是离散特征，
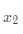是连续特征，y 是目标值。
如果选择离散特征 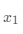，并将切分点 s 设为 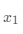是否（小于）等于 0，这时 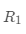包含编号为 {2} 的样本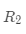， 包含编号为 {1,3,4} 的样本，求出此时的 
：
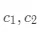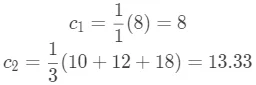
再求出此时的平方误差：
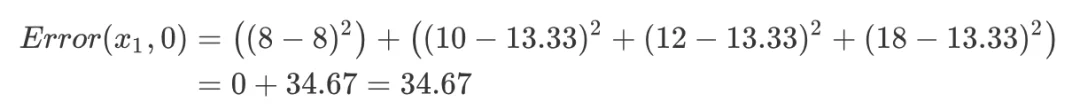
如果选择连续特征 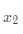，切分点可以为 2.5 或 3.5，将最后求出的 
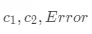结果列举出来：
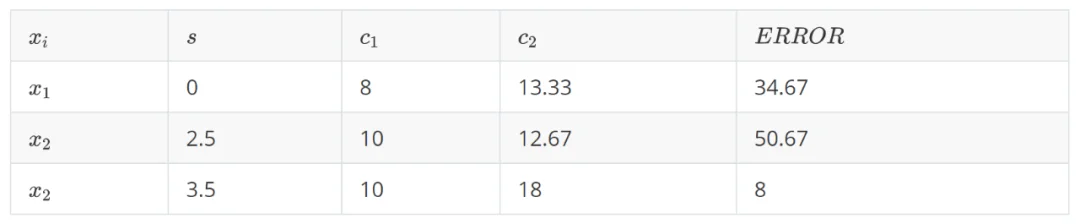
可以看到，当前最优划分特征为 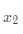，切分点为 3.5。这时候，回归树 
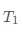为：
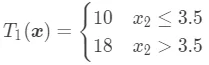整个回归树：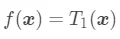
这时候用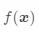 
拟合数据集中的目标值，得到的残差如下：
可以看到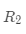， 结点下的样本（编号为
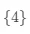）的残差为 0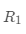， 结点下的样本（编号为
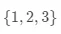）的残差分别是 0, -2, 2 。我们针对 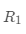结点（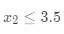
）继续划分。这时候拟合的目标值为残差了。
可以看到，当前最优划分特征为 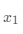，切分点为 0。这时候，回归树 
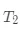为：
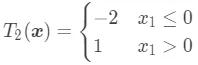
整个回归树为：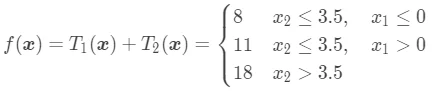
从上面例子中可以看到，决策树从数学上讲就是一个分段函数，它的参数描述的是分段方法。
参考：
决策树—回归
(https://blog.csdn.net/Albert201605/article/details/81865261)
手把手教你实现一个分类回归树
(https://www.ibm.com/developerworks/cn/analytics/library/machine-learning-hands-on5-cart-tree/index.html)