题目
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项。
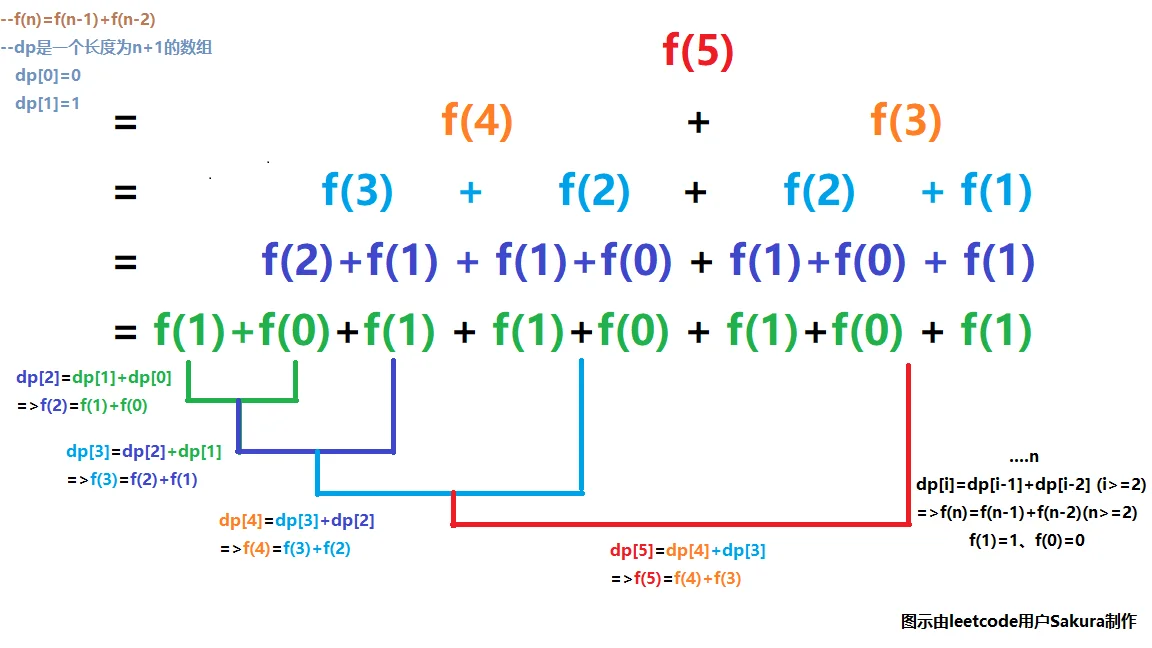
斐波那契数列的定义如下:F(0) = 0, F(1) = 1 F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和1 开始,之后的斐波那契数就是由之前的两数相加而得出。答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
注意:答案需要取模 1e9+7(1000000007),如计算初始结果>1000000007,则返回 1。
解题思路放在最后面解释!
解法一:动态规划
写法一:
–执行用时:0 ms --内存消耗:2 MB
func fib(n int) int {
if n==0 ||n==1{
return n
}
dp:=make([]int,n+1)
dp[0]=0
dp[1]=1
for i:=2;i<=n;i++{
dp[i]=(dp[i-1]+dp[i-2])%1000000007
}
return dp[n]
}
写法二:
–执行用时:0 ms --内存消耗:1.9 MB
func fib(n int) int {
if n==0 ||n==1{
return n
}
var (
a=0
b=1
temp int
)
for i:=2;i<=n;i++{
temp = b
b = (a + b)%1000000007
a = temp
}
return b
}
解法二:递归(递归会报“超出时间限制”)
func fib(n int) int {
if n==0 || n==1{
return n
}
return fib(n-1)+fib(n-2)
}
解法一的解题思路
1.什么是动态规划?
简单来讲就是一个问题的子问题的结果会被重复利用,也是一种递归思想。
2.假设n=5,下面我用我做的一张图来解释
可得:
在LeetCode该题中,我也有提交题解,欢迎查看。昵称:Sakura。
