上一篇文章讲解了冒泡排序的优化,现在来总结一下快速排序。快速排序作为经典的排序算法之一,其实也用到了冒泡排序的思想,冒泡排序是每一轮将最大(最小)的元素放到一端,而快速排序是每一轮找出比基准元素大、小的所有元素,然后放在基准元素的两边。
快速排序也有很多的实现方式,包括单边循环法、双边循环法,这两种都是通过递归来实现的,除此之外,还可以通过栈来实现。
思路梳理
先简单介绍一下双边循环法的思路。
给出如下的初始数组,现在需要进行从小到大的排序,首先找到一个基准元素(我们期望每一轮排好的结果是所有比基准元素小的数字在它的左边,所有比基准元素大的数字在它的右边),这里选择第一个元素作为基准元素,然后需要两个指针,一个左指针,负责从左向右移动,一个右指针,负责从右向左移动。
双边循环法的思路是:先从right指针开始(根据个人习惯,也可以从left开始),right指向的元素如果大于或等于基准元素,则该元素不动(right指针的作用是保证它指向的元素以及它右边的元素都是大于基准元素的),然后right指针向左移动一位(进行比较下一个);如果right指针指向的元素比基准元素小,则right指针停止移动(right指针一直指向这个元素,做一个标识,直到left指针移动到比基准元素大的数字位置,然后和right指针进行交换),然后切换到left指针,如果left指向的元素小于或等于基准元素,则该元素不动,left指针继续向右移动,寻找下一个元素,如果指向的元素比基准元素大,则和right指针指向的元素进行元素交换(实现比基准元素小的数字放在它的左边,大的数字放在它的右边),然后right指针向左移动一位(之所以left指针不向右移动,是因为如果left和right指针相邻,二者同时移动,会出现right指针在left指针左边的情况),之后再从right指针开始新的一轮比较。
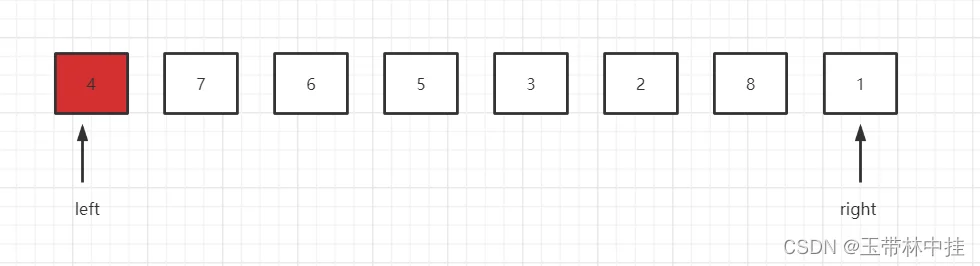
现在进行第一轮比较:
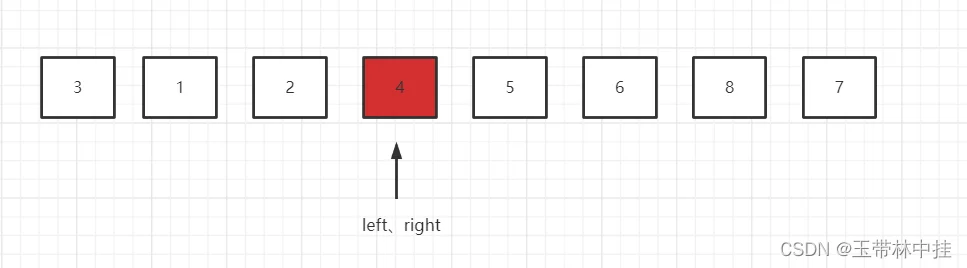
首先right指针指向的是1,1比基准元素4小,所以元素1和right指针都不动,换到left指针,left指针指向4,小于等于基准元素(也就是它自己),然后left指针向右移动一位,之后的效果图如下:
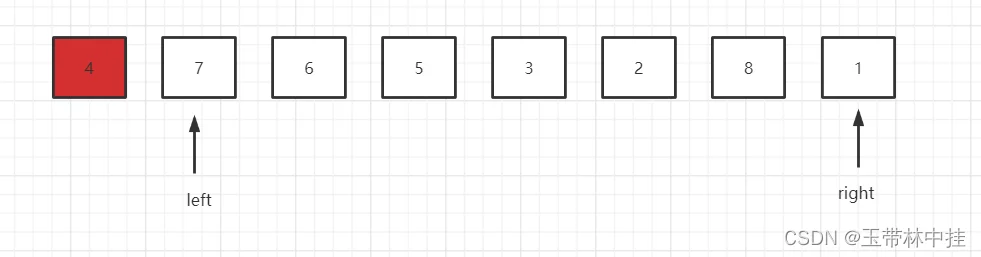
这时left指针指向7,7大于基准元素4,所以7应该在它的右面,要和right指针指向的元素进行交换,交换之后,right指针向左移动一位,开始新的比较,效果图如下:
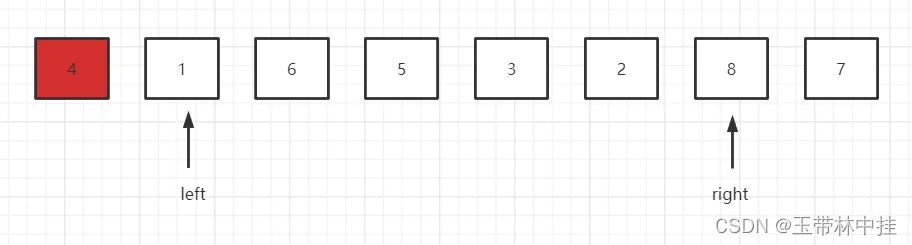
这时right指针指向元素8,8大于基准元素4,符合预期,所以继续向左移动,移动到元素2的位置,2小于基准元素4,不符合预期,所以right指针不动,换到left指针,left指针向右移动一位,移动到元素6,6大于基准元素4,不符合预期,所以和right指针进行元素交换,然后right指针向左移动一位。
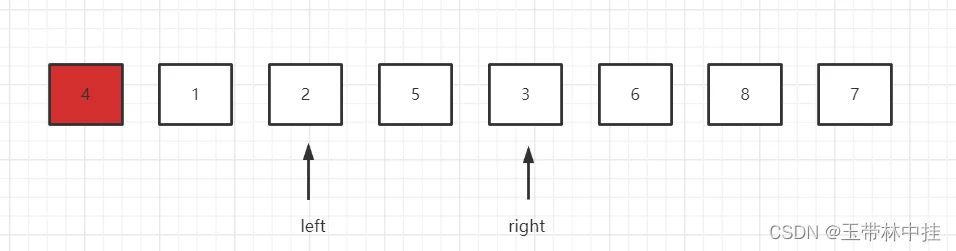
这时right指针指向元素3,3小于基准元素4,不符合预期,所以不动,切换到left指针,left指向2,小于基准元素4,符合预期,继续移动,移动到元素5,5大于4,所以和right指针交换元素,right指针并向左移动一位。
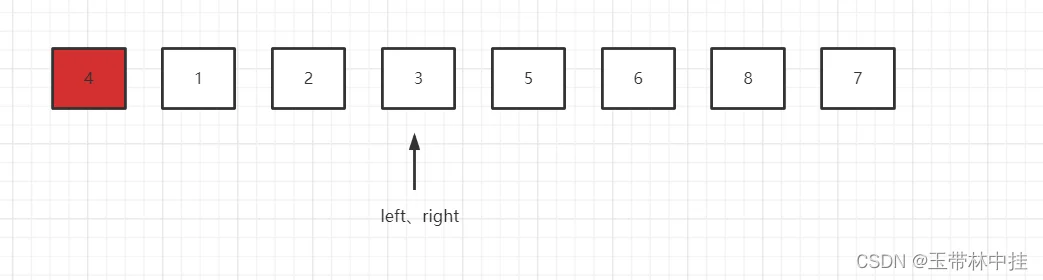
最后,基准元素再和两个指针重合的那个元素进行交换,这样就实现了比基准元素小的在它的左边,比它大的在右边。这样,第一轮就比较完毕,然后按照同样的方式比较4左右两边的数组。
代码展示
public class QuickSort {
//先确定入参:数组、起始的元素位置
public static void quickSort(int[] arr, int startIndex, int endIndex) {
//分割最小的数组为1个数字的时候就return
if (startIndex >= endIndex) {
return;
}
//基准元素取第一个位置
int pivotIndex = startIndex;
int left = startIndex;
int right = endIndex;
while (left != right) {
//从右指针开始,当右指针指向的元素大于基准元素,并且右指针指向元素的下标大于左指针
while (arr[right] > arr[pivotIndex] && right > left) {
//右指针向左移动一位
right--;
}
while (arr[left] <= arr[pivotIndex] && left < right) {
//左指针向右移动一位
left++;
}
//进行元素的交换
if (right > left) {
int temp = 0;
temp = arr[right];
arr[right] = arr[left];
arr[left] = temp;
//交换元素之后,右指针向左移动一位,从新的元素开始比较
right--;
}
//两个指针重合,就和基准元素进行交换位置
if (right == left) {
int temp = 0;
temp = arr[left];
arr[left] = arr[pivotIndex];
arr[pivotIndex] = temp;
}
}
pivotIndex = left;
//基准元素左边的循环
quickSort(arr, startIndex, pivotIndex - 1);
//右边循环
quickSort(arr, pivotIndex + 1, endIndex);
}
public static void main(String[] args) {
int[] arr = new int[]{4, 4, 9, 10, 43, 6, 5, 3, 26, 8, 1};
quickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
}
总结
right指针指向的元素以及它右边的元素都要大于等于基准元素,left指针指向的元素以及它左边的元素都要小于等于基准元素,两个指针不断的靠拢、不断的寻找不符合条件的元素,遇到不符合条件的元素就停下来,当两个指针都不符合预期时,就进行交换,就能达到符合条件的状态了。
双指针最终靠拢重合的位置也就是基准元素最后的位置,最后指针重合指向的元素在和基准元素进行交换,因此来实现比基准元素小的在它的左边,比它大的在它的右边。
双边循环法思路很清晰,但是代码比较复杂,单边循环法相对来说代码写起来要简单的多。
思路梳理
单边循环法只需要一个指针mark,该指针的作用是做一个分割点,保证该指针以及它左边的元素都要小于等于基准元素,以此来进行排序。元素不断的向右移动比较,目的是寻找小于基准元素的值,放到mark指针的左边,以此来实现分割。所以当遇到小于基准元素的值,就将mark指针向右移动一位,然后将该值和mark指针指向的元素进行交换。
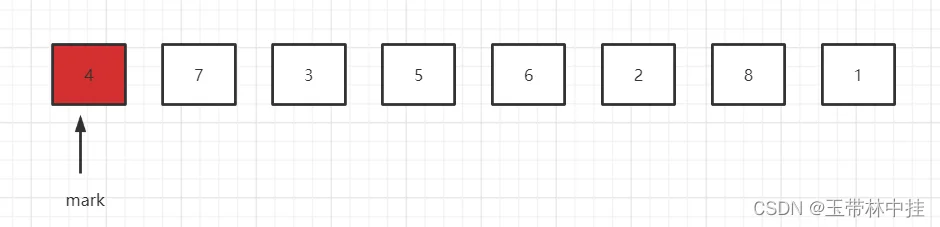
现在进行第一轮排序,基准元素取第一个数字,然后向右遍历,遍历到7的时候,7大于基准元素4,不做任何处理,继续向右遍历,遍历到3的时候,3小于基准元素4,所以它应该在mark指针的左边,这时的操作是将mark指针向右移动一位(因为多了一个比基准元素4小的元素,mark指针的左边要放小于4的元素,所以向右移动一个位置),然后将mark指针指向的元素7和3进行位置交换
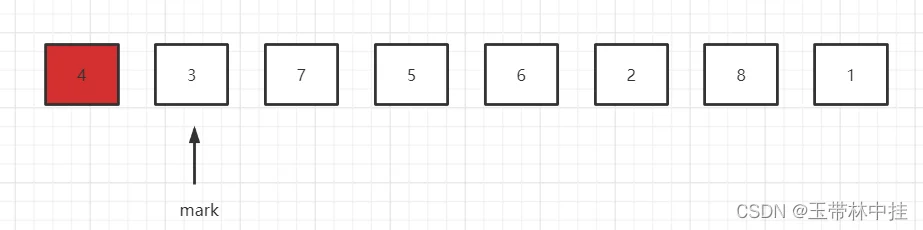
然后继续向右遍历,遍历到5、6的时候都是大于基准元素,不用管,当遍历到元素2的时候,2小于基准元素4,它应该在mark指针的左边,所以mark指针再留出一个位置,继续向右移动一位,移动到7的位置,然后和2进行元素交换。
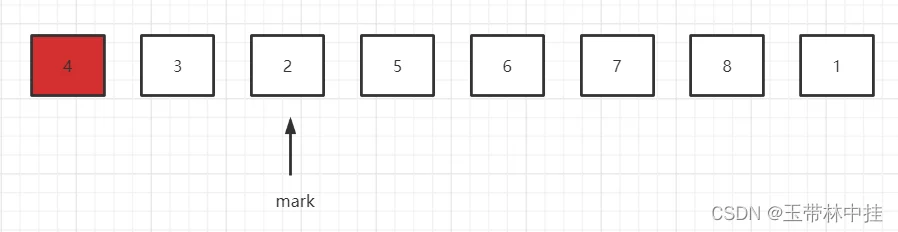
继续向右遍历,遍历到8,不用管,遍历到1,1小于基准元素4,同理,mark指针向右移动一位,指向元素5,然后和1进行元素交换
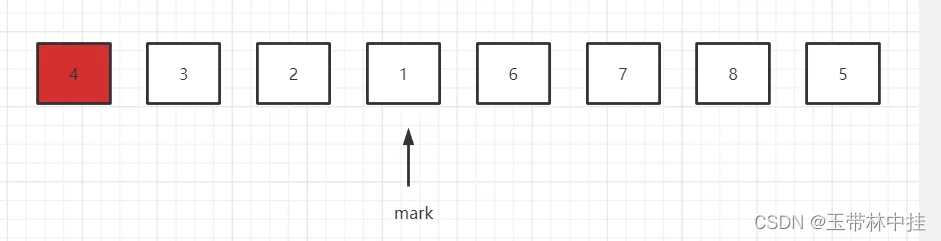
最后,基准元素4和mark指针指向的位置进行元素交换,就完成了第一轮的排序。
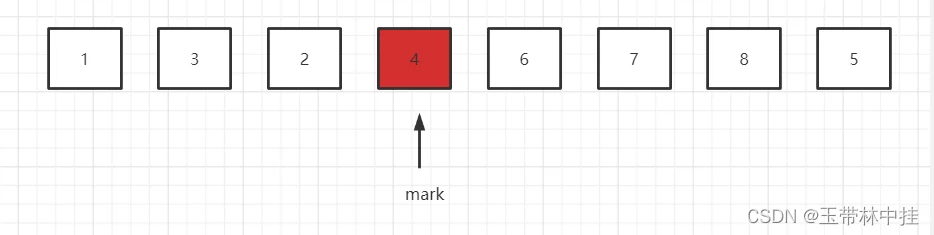
代码展示
public static void singleIndexQuickSort(int[] arr, int startIndex, int endIndex) {
//分割最小的数组为1个数字的时候就return
if (startIndex >= endIndex) return;
//指针默认取第一个
int markIndex = startIndex;
int pivotIndex = startIndex;
for (int i = startIndex; i < endIndex + 1; i++) {
//如果遍历到的值小于基准元素
if (arr[i] < arr[pivotIndex]) {
markIndex++;
int temp = arr[i];
arr[i] = arr[markIndex];
arr[markIndex] = temp;
}
}
//交换基准元素和mark指针指向的元素
int temp = arr[markIndex];
arr[markIndex] = arr[pivotIndex];
arr[pivotIndex] = temp;
//基准元素的索引下标进行更新
pivotIndex = markIndex;
//上一轮基准元素的左边
singleIndexQuickSort(arr, startIndex, pivotIndex - 1);
//上一轮基准元素的左边
singleIndexQuickSort(arr, pivotIndex + 1, endIndex);
}
public static void main(String[] args) {
int[] arr = new int[]{200, 40, 50, 4, 10, 5, 4, 7, 3, 5, 10, 9, 20, 6, 2, 8, 1};
//quickSort(arr, 0, arr.length - 1);
singleIndexQuickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
思路梳理
递归就是自己不断调用自己的方法,直到有了突破口,才停止递归。进入一个方法就等于入栈,方法执行完毕就等于出栈,栈中没有了元素,也就停止了运行,所以根据这一点,是可以通过栈来实现快速排序的。
代码展示
public static void stackQuickSort(int[] arr, int startIndex, int endIndex) {
//声明一个栈,用来存放每一个数组的起始值和结尾值。
Stack<Map<String, Integer>> mapStack = new Stack<>();
//第一轮数组的起、止下标,以hash的形式入栈
Map<String, Integer> map = new HashMap<>();
map.put("startIndex", startIndex);
map.put("endIndex", endIndex);
mapStack.push(map);
System.out.println(mapStack);
//当栈中有元素的时候
while (!mapStack.isEmpty()) {
//每一次都取最后一次入栈的元素,是基准元素的右半部分的数组
Map<String, Integer> popParam = mapStack.pop();
//获取每一轮排好序之后基准元素的位置
int pivotIndex = partition(arr, popParam.get("startIndex"), popParam.get("endIndex"));
//当基准元素左边有元素的时候就放到栈里面
if (popParam.get("startIndex") < pivotIndex) {
Map<String, Integer> leftParamMap = new HashMap<>();
leftParamMap.put("startIndex", popParam.get("startIndex"));
leftParamMap.put("endIndex", pivotIndex - 1);
//把基准元素左半部分的起止下标放到栈中
mapStack.push(leftParamMap);
}
//当基准元素右边有元素的时候就放到栈里面
if (popParam.get("endIndex") > pivotIndex) {
Map<String, Integer> rightParamMap = new HashMap<>();
rightParamMap.put("startIndex", pivotIndex + 1);
rightParamMap.put("endIndex", popParam.get("endIndex"));
//把基准元素右半部分的起止下标放到栈中
mapStack.push(rightParamMap);
}
System.out.println(mapStack);
}
}
单边循环和双边循环法用到了递归。递归的思想是要想解决A问题,就先要解决B问题,但是要想解决B问题,就先要解决C问题,这些解决问题的方法都是一致的,所以当C问题解决了,B问题、A问题也就解决了。这里是要想给一个无序的大数组排好序,先给基准元素左边的小数组排好序,要想给左边的小数组排好序,就要给这个小数组中基准元素左边的小小数组排好序,直到最小的数组,也就是这个数组只有一个数字的时候,才完成递,然后再原路返回完成归(右边同理),这样就保证每一个数字的左边都小于它,右边都大于它。所以快排的灵魂不仅仅在于排序,更多的在于递归~
递归的方法是找到每一个被分割的小数组,都从这个数组中找到基准元素,保证基准元素左右各为小、大值,直到找到最后这个小数组只有1个数;换成栈就是找到每次最后一次放入栈中的小数组,对其进行基准元素选择和排序,如果这个小数组大于1个数,则继续放到栈中。
哪里有不对的地方,希望大佬多多帮忙,感谢您的指点,共同进步~
