上一篇讲了插入调整,现在来讲删除调整。红黑树的删除无疑是最难的,抛开调整,红黑树的插入删除都跟选择二叉树一样,所以前面的步骤网上很多了,在这里只讲如何调整,以满足红黑树性质。
还是从头到尾理一下吧...
先定义一下,删除节点为d,真实删除节点为reald,顶替节点为x,x的兄弟节点即前reald的兄弟节点为w。
找到要删除的节点d。
1.若d有一个子节点,则直接用d的子节点x顶替d以达到删除的目的。此时reald就是d。
2.若没有子节点,则直接用x(此时x为空节点)顶替d。此时reald就是d。
3.若有两个子节点,则寻找d的前驱或者后继reald(也是就是d的左子树下最大的节点或者右子树下最小的节点)。将后继节点reald的值赋给d,并删除reald(用reald的子节点x顶替reald)
上面就是选择二叉树的删除方法,红黑树的话只是多一步调整步骤。
删除后调整以满足红黑树性质
若真实删除的节点reald为红色,那么删除后对红黑树性质没有影响,则不用调整。
若reald为黑色
循环条件(顶替节点x不为root,且x的颜色为黑),跳出循环后记得将x颜色赋为黑!
1.如果顶替节点x为红色,则将x变为黑色,调整结束。
2.若顶替节x点为黑色
case1 若x的兄弟节点为红色(因为x顶替了reald,也就是原reald的兄弟节点为红)
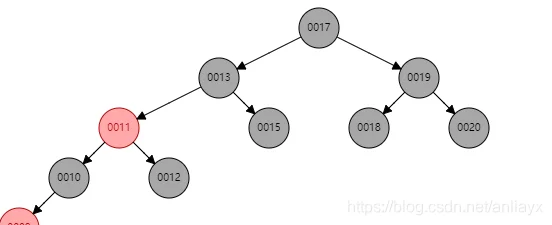 =》
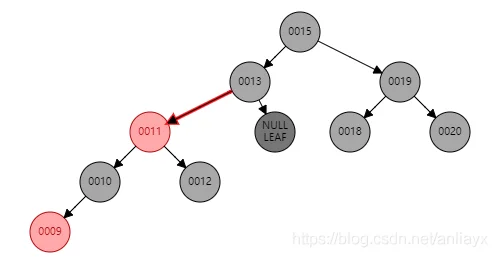
=》
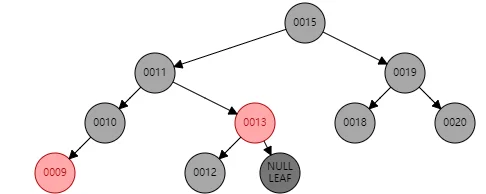
=》 
如图删除节点17,15为前驱节点,则reald为15,顶替节点x为空节点,兄弟节点11为红色。
处理方法:将兄弟节点变为黑色,x的父节13点变为红色,以x的父节点右旋(如果x是父节点的左儿子则左旋)。
旋转后,x的兄弟节点变为黑色,即上面最后一幅图的12,进入case2。这一步的目的就是让x的兄弟节点变黑。
case2 若x的兄弟节点w为黑色
case2.1 w的左右子节点都为黑 (删除17,15为前驱节点,则reald为15,顶替节点x为空节点,兄弟节点12为黑色)
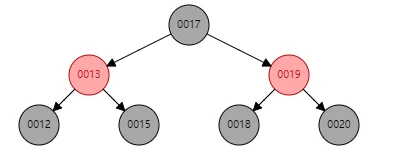 =》
=》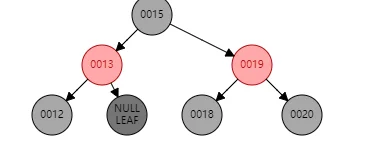
=》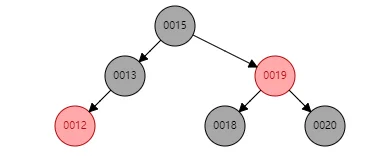
处理方法:令w为红,x=x.parent,然后就继续循环迭代(因为原先是13的右分支少了一个黑,现在是13的左右分支都少了一个黑)
case2.2 当w为左子树时,w的左节点为红(或者当w为右子树时,w的右子节点为红)
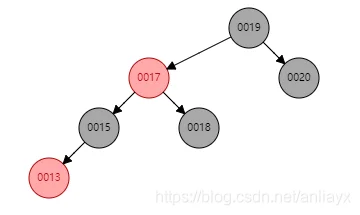 =》
=》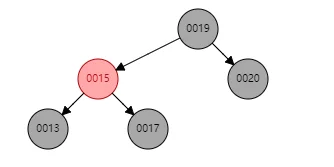
删除18,w为15。
处理方法:令w的左子树为黑(或者令w的右子树为黑),交换w和w父节点的颜色,以父节点右旋(左旋),达到平衡,令x=root跳出循环。
case2.3 当w为右子树时,w的右节点为黑,左节点肯定为红,不然就是case2.1(或者当w为左子树时,w的左子节点为黑)
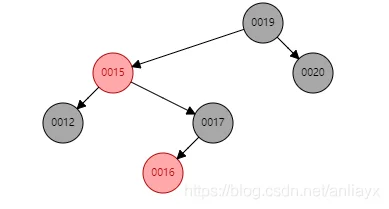 =》
=》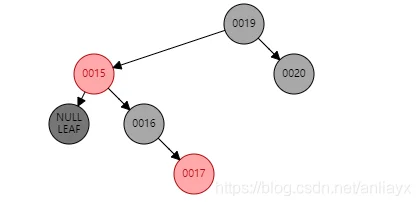
删除12,w为17,w右节点为黑。
处理方法:(目的是把情况搞成case2.2),令w为红,w的左节点为黑(或者w的右节点为黑),以W右旋(或者左旋)。得到情况case2.2。
总结:
1.如果顶替节点x为红色,则将x变为黑色,调整结束。
2.若顶替节x点为黑色
case1 若x的兄弟节点2为红色
case2 若x的兄弟节点w为黑色
case2.1 w的左右子节点都为黑
case2.2 当w为左子树时,w的左节点为红(或者当w为右子树时,w的右子节点为红)
case2.3 当w为右子树时,w的右节点为黑,左节点肯定为红,不然就是case2.1(或者当w为左子树时,w的左子节点为黑)
golang代码
func (rbt *RBTree) Delete(data float64) {
/*getMin := func(node *TreeNode) *TreeNode {
if node == nil {
return nil
}
for {
if node.lchild != nil {
node = node.lchild
} else {
return node
}
}
}*/
getMax := func(node *TreeNode) *TreeNode {
if node == NilNode {
return NilNode
}
for {
if node.rchild != NilNode {
node = node.rchild
} else {
return node
}
}
}
node := rbt.Search(data)
if node == NilNode {
return
}
dnode := node //真实删除节点reald
x := node //顶替节点
if node.lchild == NilNode && node.rchild != NilNode {
x = node.rchild
} else if node.rchild == NilNode && node.lchild != NilNode {
x = node.lchild
} else if node.rchild != NilNode && node.lchild != NilNode {
//dnode := getMin(node.rchild)
dnode = getMax(node.lchild)
node.data = dnode.data
x = dnode.lchild
} else {
x = NilNode
}
//顶替节点和删除节点的父节点关联
if dnode == rbt.root {
log.Println(dnode, rbt.root)
rbt.root = NilNode
return
} else if dnode == dnode.parent.lchild {
dnode.parent.lchild = x
} else if dnode == dnode.parent.rchild {
dnode.parent.rchild = x
}
x.parent = dnode.parent
if dnode.color == "black" {
rbt.deleteBalanceFixup(x)
}
}func (rbt *RBTree) deleteBalanceFixup(x *TreeNode) {
for x != rbt.root && x.color == "black" {
if x == x.parent.lchild { //x是左子树的情况
w := x.parent.rchild
if w.color == "red" { //case 1
w.color = "black"
x.parent.color = "red"
rbt.LeftRotate(x.parent)
w = x.parent.rchild
}
//下面是w为黑的三种情况
if w.lchild.color == "black" && w.rchild.color == "black" {
w.color = "red"
x = x.parent
} else {
if w.rchild.color == "black" {
w.lchild.color = "black"
w.color = "red"
rbt.RightRotate(w)
w = x.parent.rchild
}
//右孩子为红
w.rchild.color = "black"
w.color, x.parent.color = x.parent.color, w.color
rbt.LeftRotate(x.parent)
x = rbt.root //跳出循环
}
} else {
w := x.parent.lchild
if w.color == "red" { //case 1
w.color = "black"
x.parent.color = "red"
rbt.RightRotate(x.parent)
w = x.parent.lchild
}
//下面是w为黑的三种情况
if w.lchild.color == "black" && w.rchild.color == "black" {
w.color = "red"
x = x.parent
} else {
if w.lchild.color == "black" {
w.rchild.color = "black"
w.color = "red"
rbt.LeftRotate(w)
w = x.parent.lchild
}
//左孩子为红
w.lchild.color = "black"
w.color, x.parent.color = x.parent.color, w.color
rbt.RightRotate(x.parent)
x = rbt.root //跳出循环
}
}
}
x.color = "black"
}
