在这些系列文章中,我将主要在Golang中实现一些与分布式系统相关的著名论文。
本文讨论一种使用Red-Black树(而不是哈希表)来构建一致的哈希库的方法。
什么是一致性哈希?
一致性哈希是一种特殊的哈希,因此,当调整哈希表的大小并使用一致性哈希时,平均仅需要重新映射K / n个键,其中K是键的数量,n是插槽的数量。 我不想过多地介绍完全一致的哈希如何提供帮助,但是这里 是 几个 文章,如果您想了解更多有关它的信息。
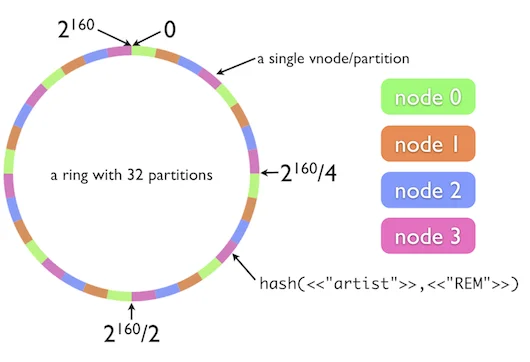
在大多数库中,实现是通过使用列表,以排序形式存储所有键以及使用哈希表确定键所属节点的哈希表来完成的。 因此,由于列表已排序,因此可以通过编写简单的搜索功能将映射到圆上的键轻松映射到节点。
这是一个从groupcache提取的简单实现(为清晰起见, 对其进行了稍微修改):
插入:
为了将节点列表添加到环哈希中,每个节点都经过m.replicas次哈希,其名称略有不同(0 node1、1 node1、2 node1…)。 哈希值添加到m.nodes切片,并且从哈希值返回到节点的映射存储在m.hashMap中。 最后,对m.nodes切片进行排序,以便我们可以在查找期间使用二进制搜索。
func (m *Map) Add(nodes ...string) { for _, n := range nodes { for i := 0; i < m.replicas; i++ { hash := int(m.hash([]byte(strconv.Itoa(i) + " " + n))) m.nodes = append(m.nodes, hash) m.hashMap[hash] = n } } sort.Ints(m.nodes) }搜索:
要查看给定密钥存储在哪个节点上,将其散列为整数。 搜索排序后的节点片,以查找大于键哈希的最小节点哈希值(如果需要环绕到圆的开始,则采用特殊情况)。 然后在映射中查找该节点哈希,以确定它来自的节点。
func (m *Map) Get(key string) string { hash := int(m.hash([]byte(key))) idx := sort.Search(len(m.keys), func(i int) bool { return m.keys[i] >= hash } ) if idx == len(m.keys) { idx = 0 } return m.hashMap[m.keys[idx]] }为什么是红黑树?
哈希表可以在O(1)时间内查找任何元素,但是自平衡树相对于哈希表(取决于用例)具有其自身的优势,原因如下:
- 自平衡树是内存有效的。 他们不会保留比他们需要更多的内存。 例如,如果哈希函数的范围为R(h)= 0 ... 100,则即使您仅哈希20个元素,也需要分配100个(指针指向)元素的数组。 如果要使用二进制搜索树存储相同的信息,则只会分配所需的空间以及一些有关链接的元数据。
- 随着数据的增长,冲突的可能性很大。 处理碰撞的方法之一是线性探测 。 这是一种开放式寻址 技术。 在这些方案中,哈希表的每个单元格都存储一个键-值对。 当哈希函数通过将新键映射到已经被另一个键占用的哈希表的单元格而引起冲突时,线性探测将在表中搜索最近的空闲位置,并将新键插入该表中。 查找的方式相同,方法是从哈希函数给定的位置开始顺序搜索表,直到找到具有匹配键的单元格或空单元格为止。 在这种情况下,插入,搜索或删除的最差时间为O(n)。
- 同样,哈希表最初需要分配的分配空间要大于输入数据的大小。 否则,将需要调整哈希表存储桶的大小,如果说要在哈希表中插入数百万个项目,这将是一项昂贵的操作。
- 哈希表中存储的元素未排序。
尽管哈希表有其自身的优势,但我发现了一个自平衡树,非常适合构建一致的哈希库的要求。 大多数自平衡树在最坏的情况下会提供O(log n)查找以进行插入,搜索和删除。 并且元素在插入时进行排序,因此无需在每次插入时对数组进行重新排序。
实作
在这篇博客中, 谷歌(Google)的人已经解释了与akamai的原始论文略有不同的变体,目的是在一致的散列圆中更好地保持键分布的一致性和一致性 。 由于自平衡树优于哈希表的优点,我想到了在Go中实现这一点。
使用一棵红黑树,插入/搜索一致的哈希圆环将如下所示:
插入:
func (r *Ring) Add(node string) {for i := 0; i < r.virtualNodes; i++ { vNodeKey := fmt.Sprintf("%s-%d", node, i) r.nodeMap[vNodeKey] = newNode(vNodeKey) hashKey := r.hash(vNodeKey) r.store.Insert(hashKey, node) } }for i := 0; i < r.virtualNodes; i++ { vNodeKey := fmt.Sprintf("%s-%d", node, i) r.nodeMap[vNodeKey] = newNode(vNodeKey) hashKey := r.hash(vNodeKey) r.store.Insert(hashKey, node) } }搜索:
搜索键几乎没有什么复杂,但是就像遍历树以查找大于键的元素(节点)一样简单。 绕过一致的哈希圆就像在Red-Black树中找到最接近的键的后继键,然后检查在要插入的特定节点上的负载是否正常一样简单,否则我们需要环绕(到达根) ,然后尝试再次搜索,直到找到可以自由接受请求的节点。
func (r *Ring) Get(key string) (string, error) {var count int var q *rbt.Node hashKey := r.hash(key) q = r.store.Nearest(hashKey)for {/* Avoid infinite recursion if all the servers are under heavy load and if user forgot to call the Done() method */ if count >= r.store.Size() { return "", ERR_HEAVY_LOAD }if hashKey > q.GetKey() { g := rbt.FindSuccessor(q) if g != nil { q = g } else { // If no successor found, return root(wrap around) q = r.store.Root() } }if r.loadOK(q.GetValue()) { break } count++h := rbt.FindSuccessor(q) if h == nil { //rewind to start of tree q = r.store.Root() } else { q = h } } return q.GetValue(), nil }完整的代码在这里 。
随时指出任何错误/错误。 如果我错过了一些事情,欢迎更多地了解此主题。
参考文献:

