红黑树详解及实现(golang)

红黑树的定义

学习、理解红黑树时，必须时紧紧刻围绕着红黑树的定义
以下是《STL源码剖析》中给出的定义：

根节点是黑色
每个节点非红即黑
如果一个节点为红色，它的子节点必为黑色
任何一个节点至NULL（树尾端）的任何路径，所含黑节点数必须相同

红黑树的节点的定义

type RbTreeColor bool
type RbTreeKeyType int
type RbTreeValueType interface{}

type RbTreeNode struct {
	Color  RbTreeColor
	Parent *RbTreeNode
	Left   *RbTreeNode
	Right  *RbTreeNode
	Key    RbTreeKeyType
	Value  RbTreeValueType
}

type RbTree struct {
	Root    *RbTreeNode
	// 定义哨兵节点，即为红黑树中的空节点
	sentinel *RbTreeNode
	pool *NodePool
	NodeNum int
}

func NewRbTree() *RbTree {
	sentinel := & RbTreeNode{}
	sentinel.Color = __BLACK
	//哨兵节点的所有指针都指向他自己
	sentinel.Left = sentinel
	sentinel.Right = sentinel
	sentinel.Parent = sentinel
	sentinel.Value = nil
	sentinel.Key = -9999
	return &RbTree{
		Root: sentinel,
		sentinel: sentinel,
		NodeNum: 0,
		pool: NewPool(),
	}
}

为了方便讨论，让我们先为某写节点取一些代名
新节点为           X
父节点为           P
祖父节点为       G
伯父节点为       S
曾祖父节点为    GG
兄弟节点为        B

旋转

左旋和右旋比较简单，不再介绍
下面是旋转，以及其他辅助函数

// FindMinNodeBy find the min value in rb tree node
func (node *RbTreeNode) FindMinNodeBy(rbTreeNilNode *RbTreeNode) *RbTreeNode {
	newNode := node
	for newNode.Left != rbTreeNilNode {
		newNode = newNode.Left
	}
	return newNode
}

func (node *RbTreeNode) FindMaxNodeBy(rbTreeNilNode *RbTreeNode) *RbTreeNode {
	newNode := node
	for newNode.Right != rbTreeNilNode {
		newNode = newNode.Right
	}
	return newNode
}

func (rbTree *RbTree) FindMax() *RbTreeNode {
	return rbTree.Root.FindMaxNodeBy(rbTree.sentinel)
}

func (rbTree *RbTree) FindMin() *RbTreeNode {
	return rbTree.Root.FindMinNodeBy(rbTree.sentinel)
}

func (rbTree *RbTree) LeftRotate(node *RbTreeNode) {
	tmpNode := node.Right
	node.Right = tmpNode.Left
	if tmpNode.Left != rbTree.sentinel {
		tmpNode.Left.Parent = node
	}
	tmpNode.Parent = node.Parent
	if node.Parent == rbTree.sentinel {
		rbTree.Root = tmpNode
	} else if node == node.Parent.Left {
		node.Parent.Left = tmpNode
	} else {
		node.Parent.Right = tmpNode
	}
	tmpNode.Left = node
	node.Parent = tmpNode
}

func (rbTree *RbTree) RightRotate(node *RbTreeNode) {
	tmpNode := node.Left
	node.Left = tmpNode.Right
	if tmpNode.Right != rbTree.sentinel {
		tmpNode.Right.Parent = node
	}
	tmpNode.Parent = node.Parent
	if node.Parent == rbTree.sentinel {
		rbTree.Root = tmpNode
	} else if node == node.Parent.Right {
		node.Parent.Right = tmpNode
	} else {
		node.Parent.Left = tmpNode
	}
	tmpNode.Right = node
	node.Parent = tmpNode
}

红黑树的插入

左旋和右旋比较简单，不再介绍
下面的红黑树的插入过程是我对照着源码的理解
插入过程分为三种情况

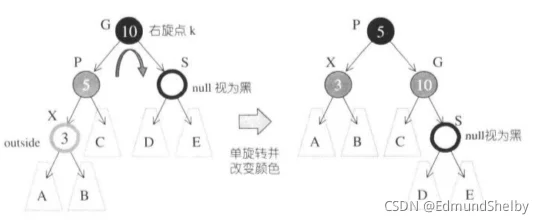
情况1：伯父节点为黑，且新节点（相对于伯父节点）为外侧插入

做法：先将新节点的父节点的颜色变为黑色，将其祖父节点变为红色，然后对其祖父节点进行一次单旋转

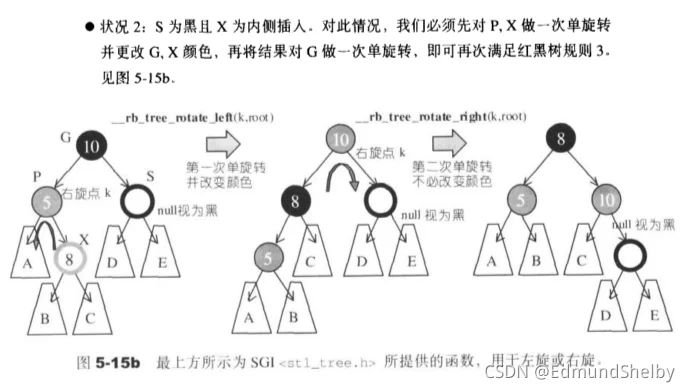
情况2：伯父节点为黑，新节点为内侧插入

做法：将原本指向新节点的指针指向其父节点，然后对其进行旋转旋转之后的指针所指向的节点的情形类似于1，重复1的操作，即可重新回复红黑树的性质，

《STL源码剖析》对这种方式的介绍，图中的第一步相当于上面所说基本操作，第二步相当于上面说的重复情况1中的操作

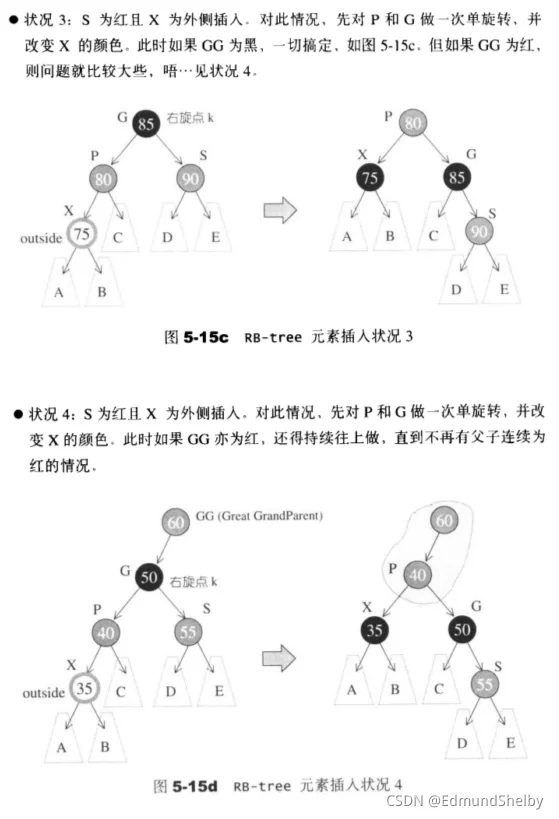
情况3：伯父节点为红色

做法：将父节点和伯父节点染黑，将祖父节点染红，并将指向新节点的指针指向其祖父节点；
看到这可能会疑惑，为什么只是简单的变色?，那就来分类讨论一下，

首先如果祖父节点为根节点，在插入修复函数退出之前，最后还有一步将根节点染黑的操作，那么这样的的话，仍然不影响红黑树的性质
如果祖父节点不为根节点，将其父节点和伯父节点染黑,不影响从祖父节点到空节点的黑节点的高度，如果祖父节点以及其父节点的颜色仍然有不符合红黑树的定义的情形，将交给下一次循环去处理

《STL源码剖析》中对伯父节点为红时的情况分为两种情况进行介绍，但仍然能归纳为这一种情况
可以看一下书中的介绍：

插入过程实现


func (rbTree *RbTree)Insert(key RbTreeKeyType,value RbTreeValueType) {
	rbTree.InsertNewNode(&RbTreeNode{Key: key,Value: value})
}

func (rbTree *RbTree) InsertNewNode(node *RbTreeNode) {
	newNodeParent := rbTree.sentinel
	tmpNode := rbTree.Root

	// 搜寻目标节点
	for tmpNode != rbTree.sentinel {
		newNodeParent = tmpNode
		if node.Key < tmpNode.Key {
			tmpNode = tmpNode.Left
		} else if node.Key > tmpNode.Key {
			tmpNode = tmpNode.Right
		} else {
			return
		}
	}

	// 把搜索到的节点作为目标节点的根节点
	node.Parent = newNodeParent

	// 如果搜索到的节点为哨兵节点，则node为根节点
	if newNodeParent == rbTree.sentinel {
		rbTree.Root = node
	// 	接下来就是判断node是父节点的左节点还是右节点
	} else if node.Key < newNodeParent.Key {
		newNodeParent.Left = node
	} else {
		newNodeParent.Right = node
	}

	// 将node的左节点和右节点都置为空
	node.Left = rbTree.sentinel
	node.Right = rbTree.sentinel
	// 新节点的颜色为红色
	node.Color = __RED
	// 进行插入修复阶段
	rbTree.insertFixUp(node)
	rbTree.NodeNum++
}

func (rbTree *RbTree) insertFixUp(node *RbTreeNode) {
	// 如果node不是根节点且，他的父节点为红色
	for node != rbTree.Root &&  node.Parent.Color == __RED {
		// 下面这一行的 if 与其 else 是相互对称的，只需要看一种情况即可
		if node.Parent == node.Parent.Parent.Left {
			// 找到node的伯父节点
			uncleNode := node.Parent.Parent.Right
			// 如果伯父节点为红色
			if uncleNode.Color == __RED {					// 情况三：
				// 在这个地方只是修改颜色和指向的原因，是将颜色调整成符合基本条件的，剩下的交给下一轮循环进行旋转
				node.Parent.Color = __BLACK        			// 将父节点的颜色变为黑色
				uncleNode.Color = __BLACK					// 将伯父节点的颜色变为黑色
				node.Parent.Parent.Color = __RED			// 将祖父节点的颜色变为红色
				node = node.Parent.Parent					// 将node指针指向其祖父节点
			// 如果伯父节点为黑色
			} else {
				if node == node.Parent.Right {				// 情况2：
					node = node.Parent						// 将原本指向新节点的指针指向其父节点
					rbTree.LeftRotate(node)					// 然后对其进行旋转
				}											// 情况1：如果刚才发生情况2，经过过处理后再次重复情况1的操作
				node.Parent.Color = __BLACK 				// 将父节点的颜色变为黑色
				node.Parent.Parent.Color = __RED         	// 将其祖父节点变为红色
				rbTree.RightRotate(node.Parent.Parent)		// 并对祖父节点进行旋转
			}
		// node的父节点是他的祖父节点的做右节点
		} else {
			// 找到node的伯父节点，其伯父节点为祖父节点的左节点
			uncleNode := node.Parent.Parent.Left
			// 伯父节点为红色
			if uncleNode.Color == __RED {
				node.Parent.Color = __BLACK				
				uncleNode.Color = __BLACK				
				node.Parent.Parent.Color = __RED		
				node = node.Parent.Parent				
			// 伯父节点为黑色
			} else {
				if node == node.Parent.Left {
					node = node.Parent
					rbTree.RightRotate(node)
				}
				node.Parent.Color = __BLACK
				node.Parent.Parent.Color = __RED
				rbTree.LeftRotate(node.Parent.Parent)
			}
		}
	}
	rbTree.Root.Color = __BLACK
}

红黑树的删除

如果要删除的节点时红色的，直接删除即可，并不会影响其红黑树的性质
下面直接讨论要删除的节点的颜色为黑色的

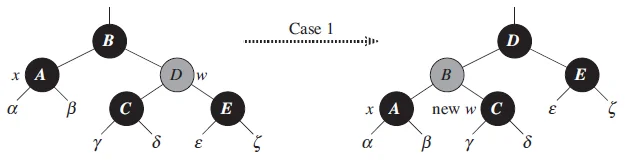
情况1：其兄弟节点是红色的

（此时x的父节点和x的兄弟节点的子节点都是黑节点）

做法：将其的兄弟节点染成黑色，将其的父节点染成红色，对其父节点进行旋转，旋转后，重新设置兄弟节点

这样做并没有直接解决问题，而是将情况1转化成情况2、情况3或者情况4从而进行进一步的处理。

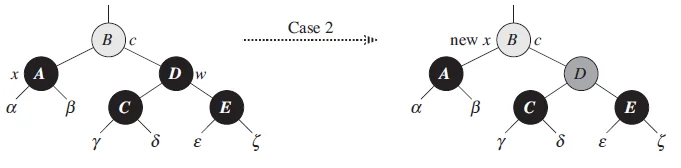
情况2：其兄弟节点是黑色，兄弟节点的两个孩子都是黑色

做法： 将其兄弟节点染成红色，将原本指向x的指针指向其父节点
先看图：

再看一下算法导论中的相关内容

概括来讲因为其兄弟节点和它的两个孩子，都是黑色的，黑色节点的的高度不平衡，所以我们将其兄弟节点染成红色。将其父节点两遍的黑高进行平衡。染色之后将原本指向X的指针指向其父节点，如果其父节点为黑色，则将会在接下来的循环中进行处理，如果其父节点为红色，则会退出循环，并在循环之后的、函数退出之前，被染成黑色

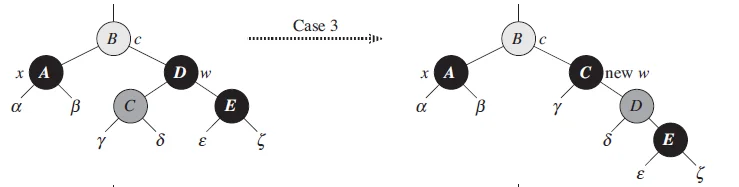
情况3：兄弟节点是黑色，兄弟节点的左孩子是红色，右孩子是黑色的

做法：将x的兄弟节点的左孩子染成黑色，将x的兄弟节点染成红色，对x的的兄弟节点进行旋转，旋转后，重新设置x的兄弟节点。

情况3也是并没有直接解决问题,而是把现有的问题转话成情况4进行解决

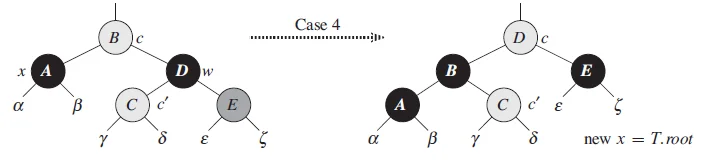
情况4：兄弟节点是黑色，兄弟节点的右孩子是红色的，兄弟节点的左孩子任意颜色

做法： 将父节点的颜色给它的兄弟节点，然后将父节点和它的兄弟节点的颜色染成黑色，然后将其父节点进行旋转，最后将原本指向x的指针指向根节点

删除部分的源码


// getReplaceNode 获取将要删除的节点的替代者
func getReplaceNode(node,sentinelNode *RbTreeNode) *RbTreeNode{
	if node.Right != sentinelNode {
		return node.Right.FindMinNodeBy(sentinelNode)
	}
	replaceNode := node.Parent
	for replaceNode != sentinelNode && node == replaceNode.Right {
		node = replaceNode
		replaceNode = replaceNode.Parent
	}
	return replaceNode
}

func (rbTree *RbTree) getNode(key RbTreeKeyType) *RbTreeNode{
	node := rbTree.Root
	for node != rbTree.sentinel {
		if key < node.Key {
			node = node.Left
		} else if key > node.Key {
			node = node.Right
		} else {
			return node
		}
	}
	return rbTree.sentinel
}

func (rbTree *RbTree) Delete(key RbTreeKeyType) {

	// ****************
	// 查找并确认关系
	// ****************
	// 获取要删除的节点
	node := rbTree.getNode(key)

	sentinelNode := rbTree.sentinel
	// 如果找到的节点为哨兵节点，则返回
	if node == sentinelNode {
		return
	}

	willDeletedNode := sentinelNode
	willDeletedChildNode := sentinelNode

	if node.Left == sentinelNode || node.Right == sentinelNode {
		// 左右孩子有一个或者全部等于空，那么直接指向这个节点
		willDeletedNode = node
	} else {
		// 要删除一个带有两个儿子的节点，我们用右子树的最小节点代替他
		willDeletedNode = getReplaceNode(node,sentinelNode)
	}

	// ****************
	// 通过调整节点之间的关系，把要删除的节点从树中剥离出来
	// ***************
	// 面对左右子树只有一个不为空的情况,要处理将要被删除的节点的孩子节点
	if willDeletedNode.Left != sentinelNode {
		willDeletedChildNode = willDeletedNode.Left
	} else if willDeletedNode.Right != sentinelNode {
		willDeletedChildNode = willDeletedNode.Right
	}


	willDeletedChildNode.Parent = willDeletedNode.Parent

	if willDeletedNode.Parent == sentinelNode {
		// 说明根节点将要被删除，所以更新根节点
		rbTree.Root = willDeletedChildNode
	} else if willDeletedNode == willDeletedNode.Parent.Left {
		// 将要被删除的节点是其父亲的左孩子，
		// 将其孩子节点变成其父亲的左孩子
		willDeletedNode.Parent.Left = willDeletedChildNode
	} else {
		// 将要被删除的节点是其父亲的右孩子，
		// 将其孩子节点变成其父亲的右孩子
		willDeletedNode.Parent.Right = willDeletedChildNode
	}

	// *********************
	// 覆盖相应的值
	// *********************
	// 因为willDeletedNode已经不再红黑树中
	// 如果将要删除的节点指针和node不指向同一块地址，则把将要willDeletedNode节点的值覆盖到node节点
	// 这样node节点就相当于在树中被删除了
	if willDeletedNode != node {
		// 赋值
		node.Key = willDeletedNode.Key
		node.Value = willDeletedNode.Value
	}

	// *********************
	// 平衡性质修复
	// *********************
	// 释放时如果将要删除的节点的颜色为红色，则不进行调整，若等于黑色，则进行调整
	if willDeletedNode.Color == __BLACK {
		rbTree.deleteFixUp(willDeletedChildNode)
	}
	// 释放tmp1节点,help GC
	willDeletedNode = nil
	// 节点数量减一
	rbTree.NodeNum--
}


func (rbTree *RbTree) deleteFixUp(node *RbTreeNode) {
	for node != rbTree.Root && node.Color == __BLACK {
		// 此if与相应的else是镜像的
		if node == node.Parent.Left {
			brotherNode := node.Parent.Right				// 找到其兄弟节点
			if brotherNode.Color == __RED { 				// 情况 1: ，x的兄弟节点是红色。(此时x的父节点和x的兄弟节点的子节点都是黑节点)。
				brotherNode.Color = __BLACK					// 将x的兄弟节点染成黑色。
				node.Parent.Color = __RED					// 将x的父节点染成红色。
				rbTree.LeftRotate(node.Parent)				// 对x的父节点进行旋转。
				brotherNode = node.Parent.Right				// 左旋后，重新设置x的兄弟节点。
			}
			// 如果左孩子和右孩子都是黑色
			if brotherNode.Left.Color == __BLACK && brotherNode.Right.Color == __BLACK {
															// 情况2：x的兄弟节点是黑色，x的兄弟节点的两个孩子都是黑色。
				brotherNode.Color = __RED					// 将x的兄弟节点染成红色。
				node = node.Parent							// 将指向x的指针指向其父节点。
			} else {
				if brotherNode.Right.Color == __BLACK {		// 情况3：x的兄弟节点是黑色；x的兄弟节点的左孩子是红色，右孩子是黑色的。
					brotherNode.Left.Color = __BLACK		// 将x兄弟节点的左孩子染成黑色。
					brotherNode.Color = __RED				// 将x兄弟节点染成红色。
					rbTree.RightRotate(brotherNode)			// 对x的兄弟节点进行右旋。
					brotherNode = node.Parent.Right			// 右旋后，重新设置x的兄弟节点。
				}											// 情况4：x的兄弟节点是黑色；x的兄弟节点的右孩子是红色的。
				brotherNode.Color = node.Parent.Color		// 将x父节点颜色 赋值给 x的兄弟节点。
				node.Parent.Color = __BLACK					// 将x父节点设为黑色。
				brotherNode.Right.Color = __BLACK			// 将x兄弟节点的右子节设为黑色。
				rbTree.LeftRotate(node.Parent)				// 对x的父节点进行左旋。
				node = rbTree.Root							// 设置node指针，指向根节点
			}
		} else {
			brotherNode := node.Parent.Left
			if brotherNode.Color == __RED {
				brotherNode.Color = __BLACK
				node.Parent.Color = __RED
				rbTree.RightRotate(node.Parent)
				brotherNode = node.Parent.Left
			}
			if brotherNode.Left.Color == __BLACK && brotherNode.Right.Color == __BLACK {
				brotherNode.Color = __RED
				node = node.Parent
			} else {
				if brotherNode.Left.Color == __BLACK {
					brotherNode.Right.Color = __BLACK
					brotherNode.Color = __RED
					rbTree.LeftRotate(brotherNode)
					brotherNode = node.Parent.Left
				}
				brotherNode.Color = node.Parent.Color
				node.Parent.Color = __BLACK
				brotherNode.Left.Color = __BLACK
				rbTree.RightRotate(node.Parent)
				node = rbTree.Root
			}
		}
	}
	node.Color = __BLACK
}

参考

插入过程参考《STL源码剖析》
删除过程参考《算法导论》以及博客：红黑树的删除操作
源码实现参考nginx中红黑树的实现和《STL源码剖析》