1.简介
R-B Tree,全称是Red-Black Tree,又称为“红黑树”,它一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色,可以是红(Red)或黑(Black)。在开发当中,红黑树的综合效率最高,复杂度也最高。
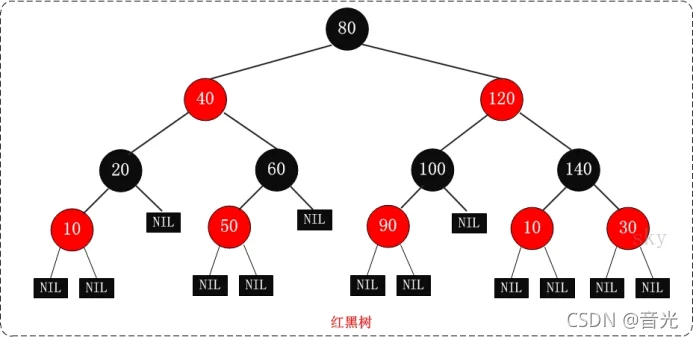
红黑树的特性: (1)每个节点或者是黑色,或者是红色。(红色代表true,黑色代表false) (2)根节点是黑色。 (3)每个叶子节点(NIL)是黑色。[注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点] (4)如果一个节点是红色的,则它的子节点必须是黑色的。(不能出现连续的红色结点) (5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
注意: (01) 特性(3)中的叶子节点,是只为空(NIL或null)的节点。 (02) 特性(5),确保没有一条路径会比其他路径长出俩倍。因而,红黑树是相对是接近平衡的二叉树。
1.1红黑树应用
红黑树的应用比较广泛,主要是用它来存储有序的数据,它的时间复杂度是O(lgn),效率非常之高。 例如,Java集合中的TreeSet和TreeMap,C++ STL中的set、map,以及Linux虚拟内存的管理,都是通过红黑树去实现的。
2.红黑树基本结构
相比较于AVL树,红黑树多出了父节点,颜色。
//定义红黑常量
const (
RED=true
BLACK=false
)
//红黑树结点结构
type RBNode struct {
Left *RBNode
Right *RBNode
Parent *RBNode
Color bool
Data interface{}
}
//红黑树结构
type RBTree struct {
Root *RBNode
NIL *RBNode
count int
}3.红黑树基本操作
//比大小
func Bigger(a,b interface{})bool{
newA:=a.(int)
newB:=b.(int)
return newA>newB
}
//初始化红黑树
func (rbt *RBTree)Init()*RBTree{
node:=&RBNode{nil,nil,nil,BLACK,nil}
return &RBTree{node,node,0}
}
//新创建红黑树
func NewRBTree()*RBTree{
return new(RBTree).Init()
}
//获取红黑树长度
func (rbt *RBTree)Len()int{
return rbt.count
}
//获取最大值结点
func (rbt *RBTree)max(x *RBNode)*RBNode{
if x==rbt.NIL{
return rbt.NIL
}
for x.Right!=rbt.NIL{
x=x.Right
}
return x
}
//获取最小值结点
func (rbt *RBTree)min(x *RBNode)*RBNode{
if x==rbt.NIL{
return rbt.NIL
}
for x.Left!=rbt.NIL{
x=x.Left
}
return x
}4.红黑树基础操作
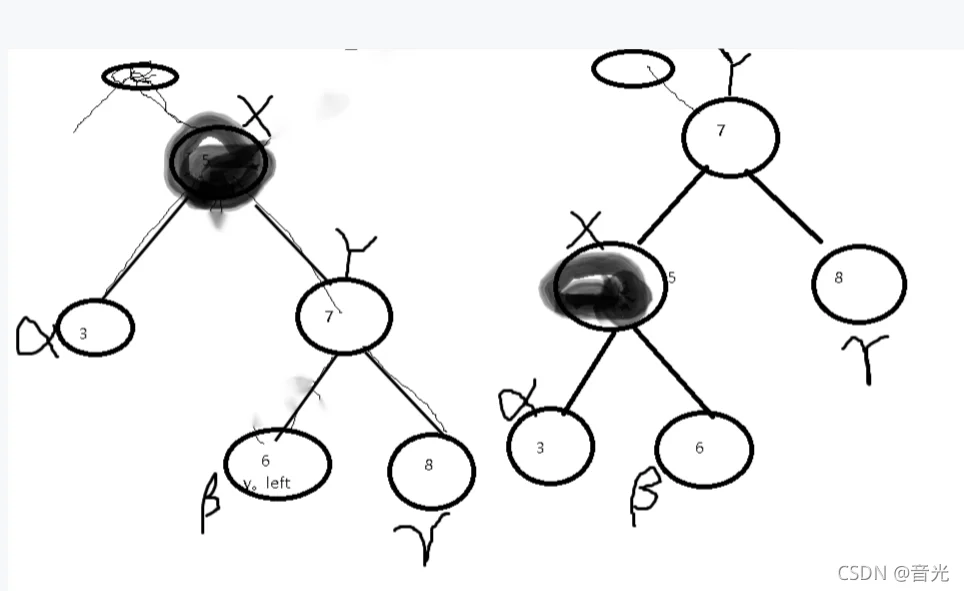
4.1 左旋
对x进行左旋,意味着"将x变成一个左节点"。左旋的伪代码《算法导论》:参考上面的示意图和下面的伪代码,理解“红黑树T的节点x进行左旋”是如何进行的。
LEFT-ROTATE(T, x)
01 y ← right[x] // 前提:这里假设x的右孩子为y。下面开始正式操作
02 right[x] ← left[y] // 将 “y的左孩子” 设为 “x的右孩子”,即 将β设为x的右孩子
03 p[left[y]] ← x // 将 “x” 设为 “y的左孩子的父亲”,即 将β的父亲设为x
04 p[y] ← p[x] // 将 “x的父亲” 设为 “y的父亲”
05 if p[x] = nil[T]
06 then root[T] ← y // 情况1:如果 “x的父亲” 是空节点,则将y设为根节点
07 else if x = left[p[x]]
08 then left[p[x]] ← y // 情况2:如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子”
09 else right[p[x]] ← y // 情况3:(x是它父节点的右孩子) 将y设为“x的父节点的右孩子”
10 left[y] ← x // 将 “x” 设为 “y的左孩子”
11 p[x] ← y // 将 “x的父节点” 设为 “y”
//左旋
func (rbt *RBTree) LeftRotate(x *RBNode){
if x.Right==rbt.NIL{
return //左旋转,右孩子不可以为空
}
y:=x.Right
x.Right=y.Left //更新x的右孩子为β
if y.Left!=rbt.NIL{
y.Left.Parent=x //更新β父节点为x
}
y.Parent=x.Parent //传递父节点 x的父节点赋给y的父节点
if x.Parent==rbt.NIL{ //x为根节点
rbt.Root=y //则y更新为根节点
}else if x==x.Parent.Left{//x在根节点左边
x.Parent.Left=y //更新y的父节点(原x的父节点)的左右孩子与y的关系 y为x父节点的左孩子
}else{//x在根节点右边
x.Parent.Right=y //更新y的父节点(原x的父节点)的左右孩子与y的关系 y为x父节点的右孩子
}
y.Left=x //更新y左孩子对x的关系 x为y的左孩子
x.Parent=y //更新x的父节点为y
}
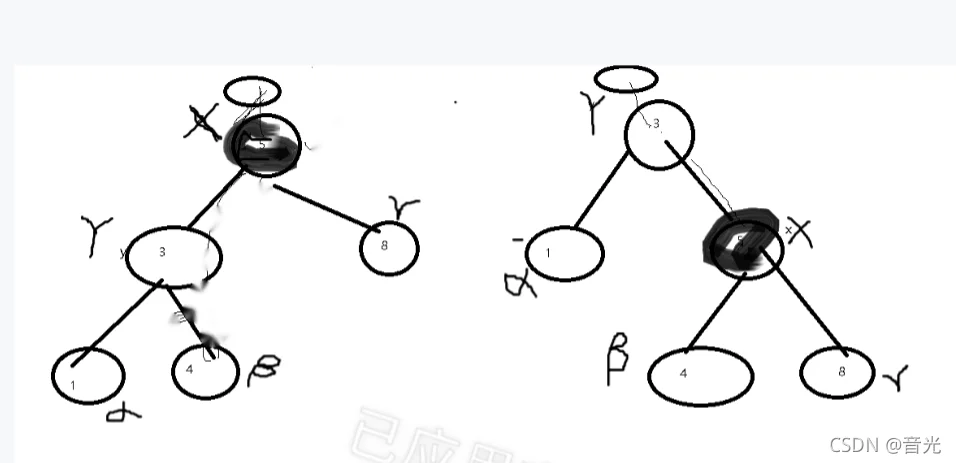
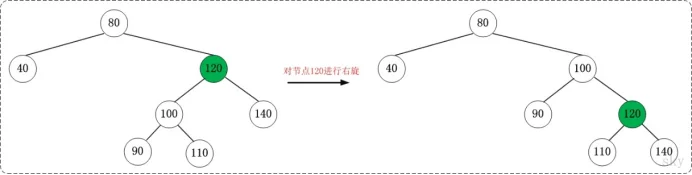
4.2右旋
对x进行左旋,意味着"将x变成一个左节点"。
右旋的伪代码《算法导论》:参考上面的示意图和下面的伪代码,理解“红黑树T的节点y进行右旋”是如何进行的。
RIGHT-ROTATE(T, y)
01 x ← left[y] // 前提:这里假设y的左孩子为x。下面开始正式操作
02 left[y] ← right[x] // 将 “x的右孩子” 设为 “y的左孩子”,即 将β设为y的左孩子
03 p[right[x]] ← y // 将 “y” 设为 “x的右孩子的父亲”,即 将β的父亲设为y
04 p[x] ← p[y] // 将 “y的父亲” 设为 “x的父亲”
05 if p[y] = nil[T]
06 then root[T] ← x // 情况1:如果 “y的父亲” 是空节点,则将x设为根节点
07 else if y = right[p[y]]
08 then right[p[y]] ← x // 情况2:如果 y是它父节点的右孩子,则将x设为“y的父节点的左孩子”
09 else left[p[y]] ← x // 情况3:(y是它父节点的左孩子) 将x设为“y的父节点的左孩子”
10 right[x] ← y // 将 “y” 设为 “x的右孩子”
11 p[y] ← x // 将 “y的父节点” 设为 “x”
//右旋
func (rbt *RBTree) RightRotate(x *RBNode){
if x.Left==rbt.NIL{
return //右旋转,左子树不可以为空
}
y:=x.Left
x.Left=y.Right //更新x的左孩子为β
if y.Right!=rbt.NIL{
y.Right.Parent=x //更新β的父节点为x
}
y.Parent=x.Parent //传递父节点,x的父节点赋给y的父节点
if x.Parent==rbt.NIL{ //x为根节点
rbt.Root=y //则y更新为根节点
}else if x==x.Parent.Left{ //x在根节点左边
x.Parent.Left=y //更新y的父节点(原x的父节点)的左右孩子与y的关系 y为x父节点的左孩子
}else{//x在根节点右边
x.Parent.Right=y //更新y的父节点(原x的父节点)的左右孩子与y的关系 y为x父节点的右孩子
}
y.Right=x //更新y的右孩子与x的关系 x为y的右孩子
x.Parent=y //更新x的父节点为y
}
4.3旋转总结
无论是左旋还是右旋,被旋转的树,在旋转前是二叉查找树,并且旋转之后仍然是一颗二叉查找树。
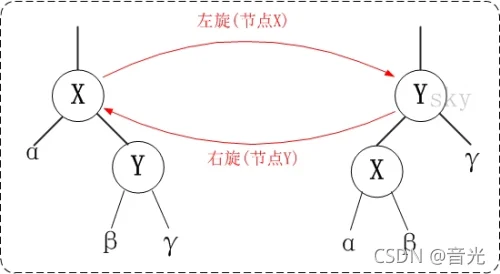
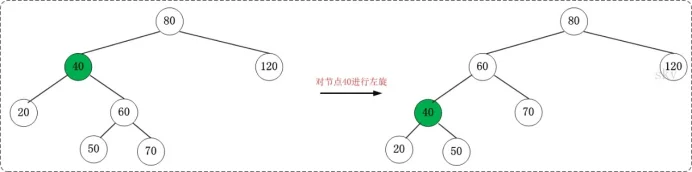
左旋示例图(以x为节点进行左旋):
z
x /
/ \ --(左旋)--> x
y z /
y
对x进行左旋,意味着,将“x的右孩子”设为“x的父亲节点”;即,将 x变成了一个左节点(x成了为z的左孩子)!。 因此,左旋中的“左”,意味着“被旋转的节点将变成一个左节点”。
右旋示例图(以x为节点进行右旋):
y
x \
/ \ --(右旋)--> x
y z \
z
对x进行右旋,意味着,将“x的左孩子”设为“x的父亲节点”;即,将 x变成了一个右节点(x成了为y的右孩子)! 因此,右旋中的“右”,意味着“被旋转的节点将变成一个右节点”。
