介绍红黑树之前,要先了解其他几种树(二叉树,二叉排序树,平衡二叉树,2-3-4(B树)),红黑树就是在其他树的变形(特别是2-3-4树,若不了解,读者要先去了解一下)。
1、性质:
性质1、每个节点是红色或黑色性质2、根节点是黑色
性质3、每个叶子结点(NIL)是黑色【这里的叶子结点,是指为空(NIL或NULL)的叶子结点!】
性质4、如果一个节点是红色的,则它的子结点必须是黑色的
性质5、从一个节点到该结点的子孙结点的所有路径上包含相同数目的黑节点
性质6:从根节点出发,每一条路径和另一条路径的高度差不超过2倍
性质7:任何一个节点插进来都会当做一个红节点插进来
2、学红黑树存在的问题?
1)为什么要有红黑树,他要解决什么问题?2)为什么要有红节点,黑节点?
3)如何保证路径的高度差不超过2倍?
答:
首先对比一下平衡二叉树,红黑树高度差不超过2倍,平均搜索效率和平衡二叉树效率一样,但最坏情况哟要差一点红黑树来解决插入AVL树效率低的问题,不平衡就需要旋转,因为性质7中红黑树任何一个节点插进来都会当做一个红节点插进来,不会有黑节点插进来,这样红黑树不会被破坏平衡(高度差不超过两倍), 不需要旋转。
为什么红结点插入进来,红黑树路径高度差不超过两倍,不会被破坏平衡?
根据性质5和性质4,如果一个节点是红色的,则它的子结点必须是黑色的,从一个节点到该节点的子孙结点的所有路径上包含相同数目的黑节点,因为路径中黑色节点个数相同,红色结点数小于黑色节点树,高度差一定不超过两倍,红黑树就是这么神奇 ,这也是为什么要有红节点,黑节点的原因。
,这也是为什么要有红节点,黑节点的原因。
二、红黑树与2-3-4树的联系:
2-3-4树和红黑树之间可以建立等价关系,2-3-4树的插入和删除过程也可以对应到红黑树的旋转与颜色变换过程。红黑树和2-3-4树之间的结点对应关系如下面的图:
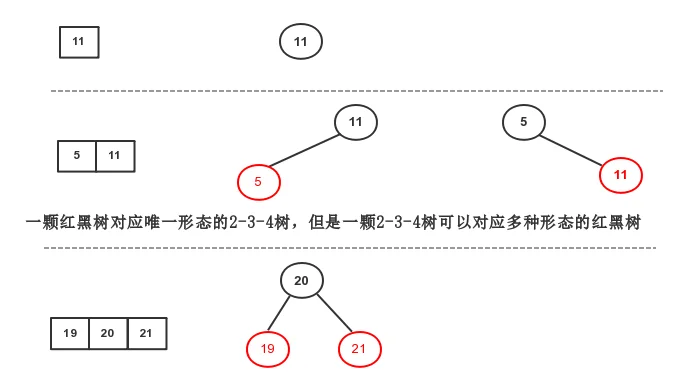
重点:一颗红黑树对应唯一形态的2-3-4树,但是一颗2-3-4树可以对应多种形态的红黑树,如下面的2-3-4树可以对应好几种红黑树,这里我只列举了两种,没有列举完。

三、红黑树插入:
1、插入节点时根节点---------------------:直接插入,将根节点变为黑色

2、插入节点父节点是黑色-----------------: 直接插入,不违反任何性质
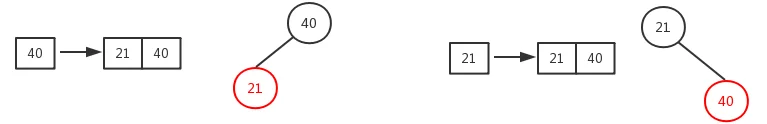
3、插入节点父节点是红色:(违反了性质4,因为插入的都被当做红色,需要调整)
3.1、插入节点父节点是红色,叔叔节点时红色-------:调整如下:
①将父结点设为黑色②将叔叔节点设为黑色③将祖父结点设为红色④将祖父结点设为当前插入结点,继续向上查看是否满足红黑树
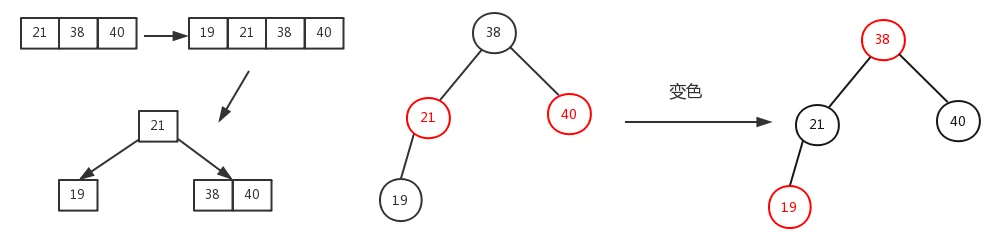
3.2、插入结点父节点是红色,叔叔节点是黑色(或无叔叔节点),当前插入结点是其父结点的左孩子-------:调整如下:
对应下面两种情况:先变色,再旋转。
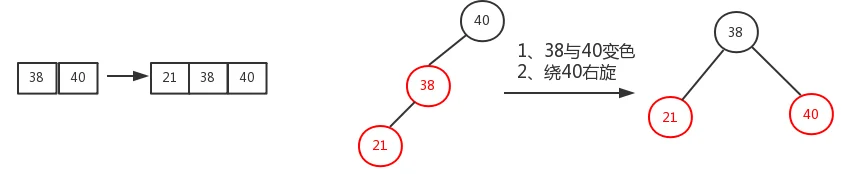

3.3、插入结点父节点是红色,叔叔节点是黑色(或无叔叔节点),当前插入结点是其父结点的左孩子-------:调整如下:
也对应下面两种情况:先变色,再旋转。


四、红黑树的删除:
1)要删除的key位于非叶子结点上,则用后继key覆盖要删除的key,然后删除该后继key。则转为以下两种情况。
2)删除节点为红色,直接删除。
3)删除节点为黑色:①删除节点有红色孩子。②删除节点无孩子。
下面分别对这些情况进行讨论。
1、删除节点为根节点,直接删除。
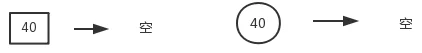
2、删除节点为红色,直接删除。

3、删除节点为黑色:下面例子都是以删除点为左孩子为例。要考虑对称情况。
3.1、删除节点为黑色,删除节点有红色孩子:让红孩子颜色变黑,然后替换要被删除的节点。
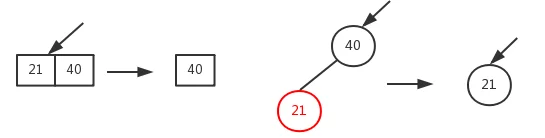
3.2、删除节点为黑色,删除节点没有孩子。这时对应2-3-4树中,要向兄弟节点借节点或与父节点 进行合并。但在进行借或合并之前要进行如下操作。判断叔叔节点是黑色还是红色。若叔叔节点是红色,想办法将叔叔节点转换为黑色。
为什么要这样做?例如下2-3-4树图,要删除3,无论是想兄弟节点借,还是与父节点合并,都是与节点11无关系的。所以要与11撇清关系。经过下面的操作。要删除的节点3的叔叔节点9成功的变成了黑色。之后无论是向兄弟节点借还是与父节点合并,都与11没有关系。

3.2.1、删除节点为黑色,删除节点没有孩子,删除节点的叔叔节点有右孩子(左孩子可有可无,但一定要有右孩子)。
对应2-3-4树中,可以向兄弟节点借。
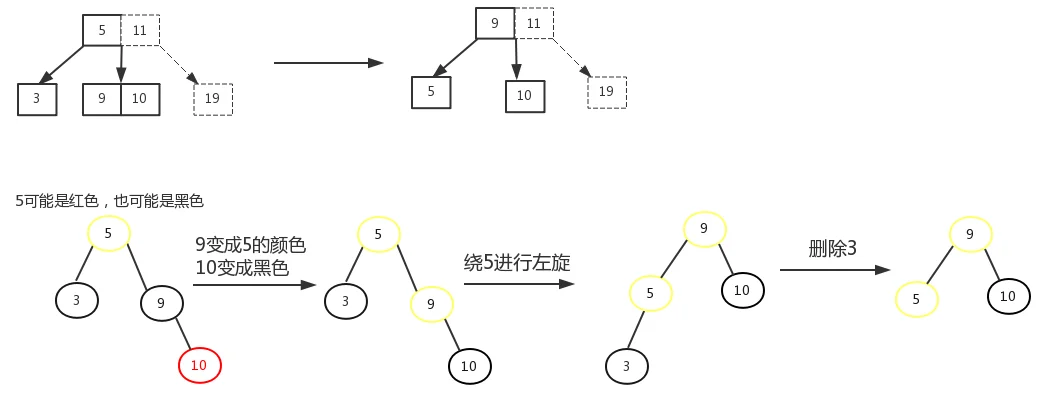
3.2.2、删除节点为黑色,删除节点没有孩子,删除节点的叔叔节点有左孩子(右孩子可有可无,但一定要有左孩子)。
对应2-3-4树中,可以向兄弟节点借。
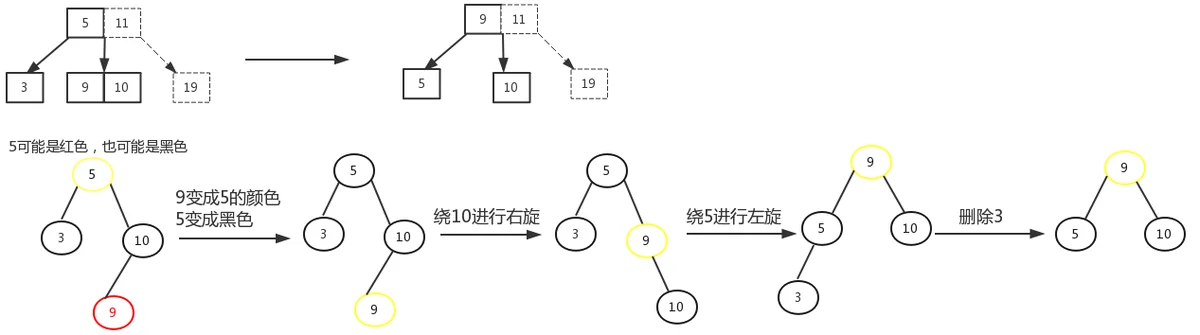
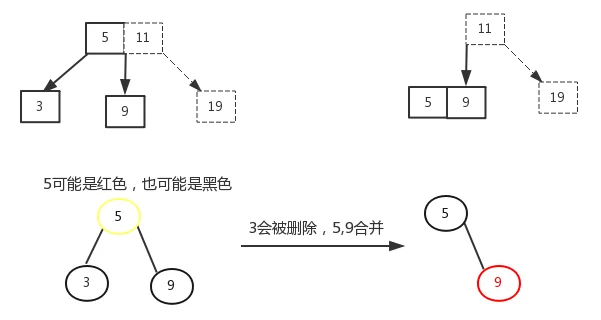
3.2.3、删除节点为黑色,删除节点没有孩子,删除节点的叔叔节点没有孩子。
对应2-3-4树中,不可以向兄弟节点借。与父节点进行合并
五、代码实现:
package main
import "fmt"
type RB struct {
value int //节点中的值
color bool //节点颜色(红色:true,黑色:false)
parent *RB //父节点的指针
left *RB //指向左孩子节点的指针
right *RB //指向右孩子节点的指针
}
func (t *RB) leftRotate() *RB { //左旋转
headNode := t.right
t.right = headNode.left
if headNode.left != nil {
headNode.left.parent = t
}
headNode.left = t
t.parent = headNode
headNode.parent = nil
return headNode
}
func (t *RB) rightRotate() *RB { //右旋转
headNode := t.left
t.left = headNode.right
if headNode.right != nil {
headNode.right.parent = t
}
headNode.right = t
t.parent = headNode
headNode.parent = nil
return headNode
}
func (t *RB) rightThenLeftRotate() *RB { //右旋转,之后左旋转
//以失衡点右结点先右旋转
sonHeadNode := t.right.rightRotate()
t.right = sonHeadNode
sonHeadNode.parent = t
//再以失衡点左旋转
return t.leftRotate()
}
func (t *RB) LeftThenRightRotate() *RB { //左旋转,之后右旋转
//以失衡点左结点先左旋转
sonHeadNode := t.left.leftRotate()
t.left = sonHeadNode
sonHeadNode.parent = t
//再以失衡点左旋转
return t.rightRotate()
}
//在红黑树中查找关键字为value的节点,返回查找成功和所在该节点
func (t *RB) Search(value int) (bool,*RB) {
if t == nil {
return false,nil
}
node := &RB{}
for t != nil {
if value < t.value {
if t.left == nil {
node = t
}
t = t.left
} else if value > t.value {
if t.right == nil {
node = t
}
t = t.right
}else {
return true,t
}
}
return false,node
}
//找兄弟节点
func (t *RB) GetBrother() *RB {
brother := &RB{}
if t.parent.left != nil && t.parent.left.value == t.value {
brother = t.parent.right
}else if t.parent.right != nil && t.parent.right.value == t.value{
brother = t.parent.left
}
return brother
}
//找祖父节点
func (t *RB) Getgrandfather() *RB {
return t.parent.parent
}
//添加完元素查看是否满足红黑树
func (t *RB) InsertAdjust() *RB {
for t.color == true {
lchild := t.left
rchild := t.right
parent := t.parent
brother := t.GetBrother()
if brother != nil && brother.color == true { //3.1插入节点叔叔节点是红色
t.color = false
brother.color = false
parent.color = true
if parent.parent != nil {
t = parent.parent
}else {
parent.color = false
}
}else { //3.2插入节点叔叔节点是黑色,或没有叔叔节点
if lchild != nil && parent.left == t{ //3.2.1、LLL型
t.color = false
parent.color = true
if parent.parent != nil {
te := parent.parent
if te.left.value == parent.value {
te.left = parent.rightRotate()
te.left.parent = te
return te.left
}else {
te.right = parent.rightRotate()
te.right.parent = te
return te.right
}
}else {
return parent.rightRotate()
}
} else if rchild != nil && parent.right == t{ //3.2.2、RRR型
t.color = false
parent.color = true
if parent.parent != nil {
te := parent.parent
if te.left.value == parent.value {
te.left = parent.leftRotate()
te.left.parent = te
return te.left
}else {
te.right = parent.leftRotate()
te.right.parent = te
return te.right
}
}else {
return parent.leftRotate()
}
}else if rchild != nil && parent.left == t{ //3.2.3、LLR型
rchild.color = false
parent.color = true
if parent.parent != nil {
te := parent.parent
if te.left.value == parent.value {
te.left = parent.LeftThenRightRotate()
te.left.parent = te
return te.left
}else {
te.right = parent.LeftThenRightRotate()
te.right.parent = te
return te.right
}
}else {
return parent.LeftThenRightRotate()
}
}else if lchild != nil && parent.right == t{ //3.2.4、RRL型
lchild.color = false
parent.color = true
if parent.parent != nil {
te := parent.parent
if parent.parent.left.value == parent.value {
te.left = parent.rightThenLeftRotate()
te.left.parent = te
return te.left
}else {
te.right = parent.rightThenLeftRotate()
te.right.parent = te
return te.right
}
}else {
return parent.rightThenLeftRotate()
}
}
}
}
return t
}
//添加元素
func (t *RB) Insert(value int) *RB {
ok,node:= t.Search(value) //在整颗树中找到要插入到哪个节点中
if !ok && node ==nil { //1、树为空,直接插入黑根节点
return &RB{value,false,nil,nil,nil}
}
if !ok {
newNode := RB{value, true, nil, nil, nil}
if value < node.value {
node.left = &newNode
newNode.parent = node
} else {
node.right = &newNode
newNode.parent = node
} //2、插入节点父节点是黑色,不管
if node.color == true {//3、插入节点父节点是红色,要管了
t = node.InsertAdjust()
}
}
for t.parent != nil {
t = t.parent
//fmt.Println(t)
}
return t
}
/*删除关键字
1)要删除的key位于非叶子结点上,则用后继key覆盖要删除的key,然后删除该后继key。
2)如果删除红色,直接删除。
3)删除黑色:
3.1)对照2-3-4:节点内删除,将红色孩子节点变成黑色,补上。
3.2)对照2-3-4:节点内无多余的,兄弟节点有多余的,进行借。
3.3)对照2-3-4:节点内无多余的,兄弟节点也没多余的,进行合并。
*/
//查找后继最小结点
func (t *RB) getMinNode() *RB {
if t == nil {
return nil
}else {
if t.right != nil {
t = t.right
}
for t.left != nil {
t = t.left
}
}
return t
}
//删除完元素查看是否满足红黑树
func (t *RB) DeleteAdjust() *RB {
return nil
}
//改变叔叔节点为黑色
func (t *RB) ChangeUncleToBlack() (*RB,*RB){
parent := t.parent
if t == parent.left {//被删除节点在父节点的左边
uncle := parent.right
if uncle == nil {
return parent,t
}else if uncle.color == true {
uncle.color = false
parent.color = true
node := parent.leftRotate()
next := node.left.left
return node,next
}
}else {//对称,被删除节点在父节点的右边
uncle := parent.left
if uncle == nil {
return parent,t
}else if uncle.color == true {
uncle.color = false
parent.color = true
node := parent.rightRotate()
next := node.right.right
return node,next
}
}
return parent,t
}
//删除黑色叶子节点
func (t *RB) DeleteSingleBlack() *RB{
parent := t.parent
if t == parent.left {
parent.left = nil
uncle := parent.right
if uncle != nil && uncle.left != nil {//相当于(2-3-4树中)兄弟节点有多余的左红孩子借给它
uncle.left.color = parent.color
parent.color = false
parent.right = uncle.rightRotate()
parent.right.parent = parent
if parent.parent != nil{
te := parent.parent
if te.left == parent {
te.left = parent.leftRotate()
te.left.parent = te
}else {
te.right = parent.leftRotate()
te.right.parent = te
}
return te
}else {
return parent.leftRotate()
}
}else if uncle != nil && uncle.right != nil{//相当于(2-3-4树中)兄弟节点有多余的右红孩子借给它
uncle.color = parent.color
uncle.right.color = false
parent.color = false
if parent.parent != nil{
te := parent.parent
if te.left == parent {
te.left = parent.leftRotate()
te.left.parent = te
}else {
te.right = parent.leftRotate()
te.right.parent = te
}
return te
}else {
return parent.leftRotate()
}
}else {//相当于(2-3-4树中)兄弟节点没有多余的红孩子借给它,合并.及叔叔节点没有孩子
parent.color = false
parent.right.color = true
return parent
}
}else { //与上面的对称,删除点在右边
parent.right = nil
uncle := parent.left
if uncle.right != nil {//相当于(2-3-4树中)兄弟节点有多余的右红孩子借给它
uncle.right.color = parent.color
parent.color = false
parent.left = uncle.leftRotate()
if parent.parent != nil{
te := parent.parent
if te.left == parent {
te.left = parent.rightRotate()
te.left.parent = te
}else {
te.right = parent.rightRotate()
te.right.parent = te
}
return te
}else {
return parent.rightRotate()
}
}else if uncle.left != nil{//相当于(2-3-4树中)兄弟节点有多余的左红孩子借给它
uncle.color = parent.color
uncle.left.color = false
parent.color = false
if parent.parent != nil{
te := parent.parent
if te.left == parent {
te.left = parent.rightRotate()
te.left.parent = te
}else {
te.right = parent.rightRotate()
te.right.parent = te.right
}
return te
}else {
return parent.rightRotate()
}
}else {//相当于(2-3-4树中)兄弟节点没有多余的红孩子借给它,合并.及叔叔节点没有孩子
parent.color = false
parent.left.color = true
return parent
}
}
return t
}
//在整颗树中删除关键字
func (t *RB) Delete(value int) *RB{
ok,nodeTemp:= t.Search(value) //先
if nodeTemp == nil {
return nil
}
node := nodeTemp.getMinNode() //后继最小节点
nodeTemp.value = node.value
if ok {
if node.parent == nil { //1、删除根节点,返回空树
return nil
}else {
if node.color == true { //2、删除红色结点,直接删除
father := node.parent
father.left = nil
father.right = nil
node = father
}else if node.left != nil || node.right != nil {//3.1、删除黑色节点有红孩子
if node.left != nil {
node.value = node.left.value
node.left = nil
}else {
node.value = node.right.value
node.right = nil
}
}else { //3.2&3.3、黑色节点没有孩子,(在2-3-4树)需要向兄弟借,或与父节点合并
//此时(在红黑树中)被删除节点的叔叔节点有可能是红色,有可能是黑色。都调整为黑色
if grandfather:=node.Getgrandfather();grandfather!= nil {
if grandfather.left.value == node.parent.value {
grandfather.left,node= node.ChangeUncleToBlack()
grandfather.left.parent = grandfather
}else {
grandfather.right,node = node.ChangeUncleToBlack()
grandfather.right.parent = grandfather
}
}else {
_,node = node.ChangeUncleToBlack()
}
node = node.DeleteSingleBlack()//现在兄弟节点都是黑的了,再删除
}
}
}
for node.parent != nil {
node = node.parent
}
return node
}
//先根遍历,递归
func (t *RB) PreTraverse(){
if t != nil {
fmt.Printf("%d %v %v\n",t.value,t.color,t.parent)
t.left.PreTraverse()
t.right.PreTraverse()
}
}
func main(){
root := &RB{12,false,nil,nil,nil}
root = root.Insert(1)
root = root.Insert(9)
root = root.Insert(2)
root = root.Insert(0)
root = root.Insert(11)
root = root.Insert(7)
root = root.Insert(19)
root = root.Insert(4)
root = root.Insert(15)
root = root.Insert(18)
root = root.Insert(5)
root = root.Insert(14)
root = root.Insert(13)
root = root.Insert(10)
root = root.Insert(16)
root.PreTraverse()
fmt.Println("after delete:")
root = root.Delete(12)
root = root.Delete(1)
root = root.Delete(9)
root = root.Delete(2)
root = root.Delete(0)
root = root.Delete(11)
root = root.Delete(7)
root = root.Delete(19)
root = root.Delete(4)
root = root.Delete(15)
root = root.Delete(18)
root = root.Delete(5)
root = root.Delete(14)
root = root.Delete(13)
root = root.Delete(10)
root = root.Delete(16)
root.PreTraverse()
}