什么是二叉树？

在计算机科学中，二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”和“右子树”，左子树和右子树同时也是二叉树。二叉树的子树有左右之分，并且次序不能任意颠倒。二叉树是递归定义的，所以一般二叉树的相关题目也都可以使用递归的思想来解决，当然也有一些可以使用非递归的思想解决，我下面列出的一些算法有些采用了递归，有些是非递归的。

什么是二叉排序树？

二叉排序树又叫二叉查找树或者二叉搜索树，它首先是一个二叉树，而且必须满足下面的条件：

1）若左子树不空，则左子树上所有结点的值均小于它的根节点的值；

2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值

3）左、右子树也分别为二叉排序树

4）没有键值相等的节点（？可能是因为不好处理键值相等的节点到底是左节点还是右节点吧）

先序遍历 （根 左 右）

先访问根，再遍历左子树，再遍历右子树。典型的递归思想。

中序遍历（左 根 右）

先遍历左子树，再访问根，再遍历右子树。

对于二叉排序树来说，中序遍历得到的序列是一个从小到大排序好的序列。

后序遍历 （左 右 根）

先遍历左子树，再遍历右子树，再访问根

B树、B+树

参考： https://www.cnblogs.com/vincently/p/4526560.html

小结：

B-Tree它能够存储数据、对其进行排序并允许以O(log n)的时间复杂度运行进行查找、顺序读取、插入和删除的数据结构

Mysql 数据库的存储结构就是B-Tree 和B+ Tree

B树是2-3树的一种扩展，他允许一个节点有多于2个的元素。

B树的插入及平衡化操作和2-3树很相似

2-3树介绍：

2-3树是最简单的B-树（或-树）结构，其每个非叶节点都有两个或三个子女，而且所有叶都在统一层上。2-3树不是二叉树，其节点可拥有3个孩子。不过，2-3树与满二叉树相似。若某棵2-3树不包含3-节点，则看上去像满二叉树，其所有内部节点都可有两个孩子，所有的叶子都在同一级别。另一方面，2-3树的一个内部节点确实有3个孩子，故比相同高度的满二叉树的节点更多。高为h的2-3树包含的节点数大于等于高度为h的满二叉树的节点数，即至少有2^h-1个节点。换一个角度分析，包含n的节点的2-3树的高度不大于[log2(n+1)](即包含n个节点的二叉树的最小高度)。 
例如，下图显示高度为3的2-3树。包含两个孩子的节点称为2-节点，二叉树中的节点都是2-节点；包含三个孩子的节点称为3-节点。
将数据项放入2-3树节点中的规则是：
（1）2-节点有两个孩子，必含一个数据项，其查找关键字大于左孩子的查找关键字，而小于右孩子的查找关键字。
（2）3-节点有三个孩子 ，必含两个数据项，其查找关键字S和L满足下列关系：S大于左孩子的查找关键字，而小于中孩子的查找关键字；L大于中孩子的查找关键字，而小于右孩子的查找关键字。
（3）叶子可以包含一个或两个数据项。

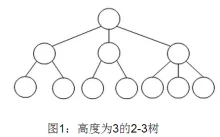
由于B+树的数据都存储在叶子结点中，分支结点均为索引，方便扫库，只需要扫一遍叶子结点即可，

但是B树因为其分支结点同样存储着数据，我们要找到具体的数据，需要进行一次中序遍历按序来扫，

所以B+树更加适合在区间查询的情况，所以通常B+树用于数据库索引，而B树则常用于文件索引。

红黑树：

参考： https://www.cnblogs.com/CarpenterLee/p/5503882.html

小结：

红黑树是一种近似平衡的二叉查找树，它能够确保任何一个节点的左右子树的高度差不会超过二者中较低那个的一陪。具体来说，红黑树是满足如下条件的二叉查找树（binary search tree）：

null