堆:
一般我们提到的是二叉堆,是一种完全二叉树,二叉堆有两种:最大堆和最小堆。特点是父节点的值大于(小于)子节点
基础知识
完全二叉树有一个性质,除了最底层,每一层都是满的,这使得堆可以利用数组来表示,如下图
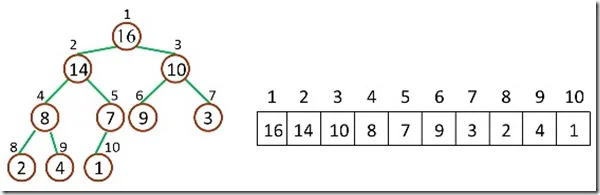
对给定某个结点下标i,可以计算出这个结点的父节点、孩子节点的下标:
父节点下标:i/2
左子节点下标:2i
右子节点下标:2i+1
但是数组都是0开始的,所以调整一下,如图:
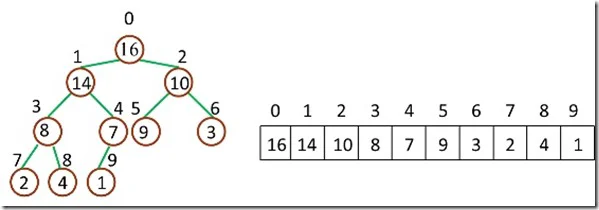
父节点下标:(i - 1)/2
左子节点下标:2i + 1
右子节点下标:2(i + 1)
维护堆
维护堆的性质过程如下图
由于调整一次,堆任然有可能违反堆性质,所以需要递归的测试,使整个堆都满足堆性质

建堆
将一个数组改造成一个堆,如图将其变成一个大顶堆

数组长度为l,首先找到(l / 2)-1 处,也就是下标为4的节点然后开始维护堆
然后自下而上,维护每一个节点,直到根节点
自下而上建堆比自上而下建堆效率高
go 实现堆排序
package main
import "fmt"
func main(){
arr:=[]int{4,8,2,1,6,9,3,5,7,8,1,4}
dui(arr)
fmt.Println(arr)
}
func swap(arr []int,a,b int){
arr[a],arr[b]=arr[b],arr[a]
}
func heapadjust(arr []int,i,m int){
son:=i*2+1
for son<m{
if son+1<m&&arr[son]<arr[son+1]{//首先判断选出左节点大还是右节点大
son++
}
if arr[i]>arr[son]{
break
}else{
swap(arr,i,son)
i=son
son=i*2+1
}
}
}
func dui(arr []int){
for i:=len(arr)/2-1;i>=0;i--{ //这里是先变成大顶堆
heapadjust(arr,i,len(arr))
}
for i:=len(arr)-1;i > 0;i--{ //将最大值与最后一个交换,然后对前i-1重新排序
swap(arr,0,i)
heapadjust(arr,0,i-1)
}
}
