如果刷力扣时突然想用 golang 了,多半是因为右手小指敲了太多分号顿感疲惫,但当我要使用堆的时候突然就懵了,出于无法原谅自己的懒惰和愚蠢,是时候做下总结了。
通常情况下,我们需要使用一个 int 类型的堆,那么通常会使用如下代码:
type hp struct {
sort.IntSlice
}
func (h *hp) Push(v interface{}) {
h.IntSlice = append(h.IntSlice, v.(int))
}
func (h *hp) Pop() interface{} {
a := h.IntSlice
v := a[len(a)-1]
h.IntSlice = a[:len(a)-1] // replicate 0 to (len(a)-1)(exclude)
return v
}(示例1)
下面要分析的是,我们只用了如此少的代码,堆的功能是如何实现的。要说明这个问题,有必要先上一段源码:
type Interface interface {
sort.Interface
Push(x interface{}) // add x as element Len()
Pop() interface{} // remove and return element Len() - 1.
}(出自container/heap/heap.go)
再看 sort.Interface:
type Interface interface {
// Len is the number of elements in the collection.
Len() int
// Less reports whether the element with
// index i should sort before the element with index j.
Less(i, j int) bool
// Swap swaps the elements with indexes i and j.
Swap(i, j int)
}这样一来明了了,要实现一个 heap,我们需要实现接口的5个抽象方法(sort.Interface 的 Len(), Less(...), Swap(...);以及 heap 接口本身的 Push(...), Pop())。
再来看下第一段代码中 heap 定义的 struct:sort.IntSlice:
// IntSlice attaches the methods of Interface to []int, sorting in increasing order.
type IntSlice []int
func (p IntSlice) Len() int { return len(p) }
func (p IntSlice) Less(i, j int) bool { return p[i] < p[j] }
func (p IntSlice) Swap(i, j int) { p[i], p[j] = p[j], p[i] }
// Sort is a convenience method.
func (p IntSlice) Sort() { Sort(p) }这里定义 IntSlice 的类型为 []int, 并且实现了 sort 接口的3个抽象方法。通常情况下,我们要使用堆,参照示例1,只需要通过构造体 struct 组合 IntSlice,并实现 heap 接口的 Push() 和 Pop() 方法即可。
当然若是需要根据自己的类型定义堆,参照 IntSlice 定义实现即可。
看看接口中的进出栈源码:
// Push pushes the element x onto the heap.
// The complexity is O(log n) where n = h.Len().
func Push(h Interface, x interface{}) {
h.Push(x) /* invoke the method that implemented by our own */
up(h, h.Len()-1) /* rise the new element to the appropriate position */
}
// Pop removes and returns the minimum element (according to Less) from the heap.
// The complexity is O(log n) where n = h.Len().
// Pop is equivalent to Remove(h, 0).
func Pop(h Interface) interface{} {
n := h.Len() - 1
h.Swap(0, n) /* exchange index 0 and index n */
down(h, 0, n) /* sink index 0 (old index n) to appropriate position*/
return h.Pop() /* invoke the method that implemented by our own */
}参考相关注释,可以看出在调用我们自己实现的 Push(), Pop() 方法时源码中已经做了相应的上浮(up)下沉(down)处理确保堆的有序性。因此,我们自己实现 Push(), Pop() 时只需要实现最简单的追加,删除操作即可。需要注意的是:实现 Pop() 时,需要移除切片的尾元素。
看到上面这段代码,不知道你是否和笔者有同样的疑惑:Push() 时做了上浮(up)操作已经保证了有序性,为何 Pop() 时还要做下沉(down)操作再次确保有序性?此操作是否多余?
要回答这个问题,读者不妨了解下 二叉堆-优先队列。这里我简单给出下逻辑和结论:
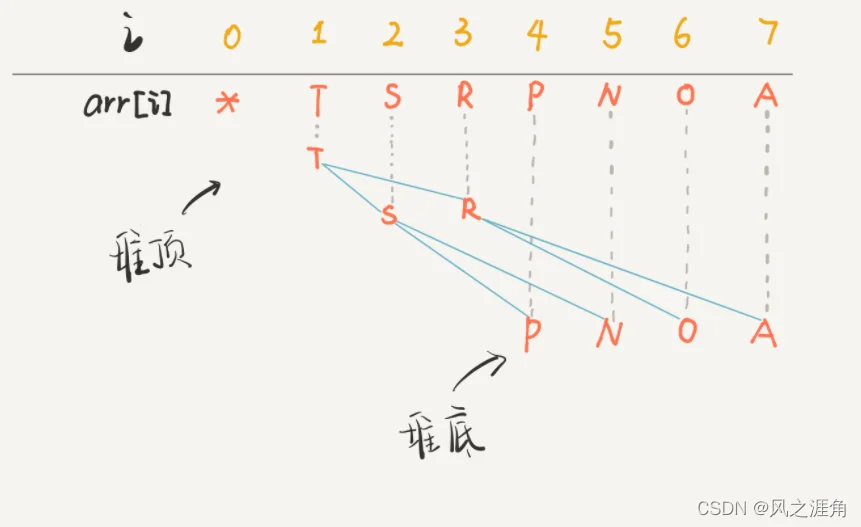
首先要区分两个概念:有序性 和 堆的有序性,有序性是指下标连续且有序,堆的有序性是指每个子节点必须小于等于其父节点,参考下图,堆虽是基于数组的实现,但其父子节点的下标并不连续。
我们知道 二叉堆 Push() 和 Pop() 的复杂度 均为 O(log n), 先看下 Push() 时 up() 的源码:
func up(h Interface, j int) {
for {
i := (j - 1) / 2 // parent
if i == j || !h.Less(j, i) {
break
}
h.Swap(i, j)
j = i
}
}上浮时,只交换 除2 后的下标!!down() 同理。而在我们自己实现的 Push() Pop() 中只是简单追加,移除了数组的尾元素,这样就破坏了堆的有序性!Push() 时的 up() 和 Pop() 时的 down()是为了保证堆的有序性!
