一、什么是堆排序
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。
排序的过程主要是由构建初始堆交换堆顶元素和末尾元素并重建堆两部分组成。其中构建初始堆经推导复杂度为O(n),在交换并重建堆的过程中,需交换n-1次,而重建堆的过程中,根据完全二叉树的性质,[log2(n-1),log2(n-2)…1]逐步递减,近似为nlogn。所以堆排序时间复杂度一般认为就是O(nlogn)级。
升序使用大顶堆,每次将末尾值交换,没构建一次大顶堆,整体数组减1。这样就完成了升序排序,降序排序的话使用小顶堆。
二、堆的特性
大顶堆:每个结点的值都大于或等于其左右孩子结点的值
小顶堆:每个结点的值都小于或等于其左右孩子结点的值
根据对的特性来形成公式就是,节点为i的话
大顶堆: arr[i]>=arr[2i+1] && arr[i]>=arr[2i+2]
小顶堆:arr[i]<=arr[2i+1] && arr[i]<=arr[2i+2]
构建堆都是从堆的最后一个root节点开始也就是(len(arr)-1)/2
三、实例
例如我们对数组{2,28,6,15,26,22,9,10,18,233,8}进行降序排列
1、首先构建一个小顶堆,数组默认的图如下
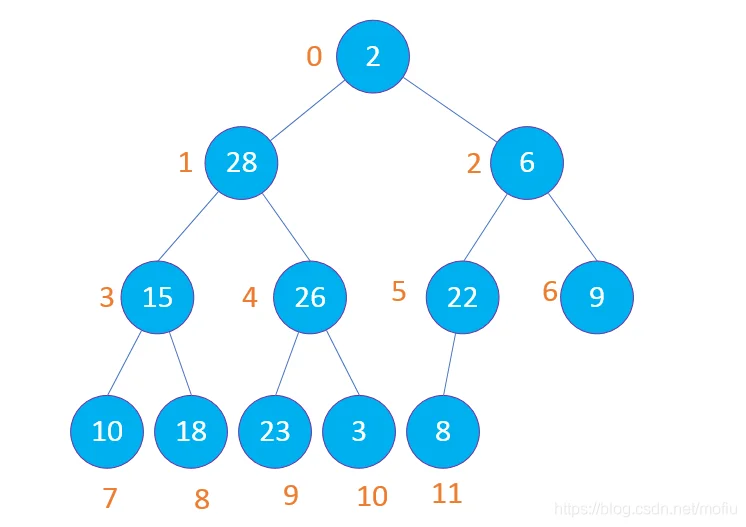
第一个需要比较的root节点为(len(arr)-1)/2,也就是5节点,因为只有一个子节点,所以只需要比较(2*5+1)节点
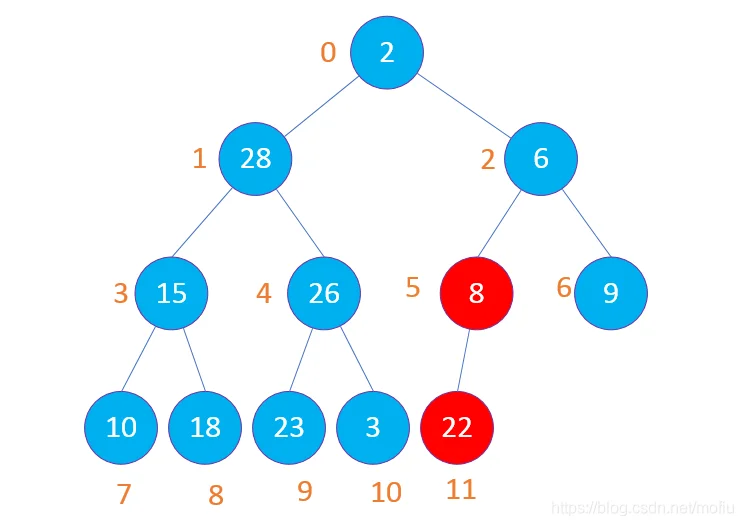
然后比较(4,9,10)节点比较,先比较9和10节点,选择较小的节点与4节点比较,结果如下图
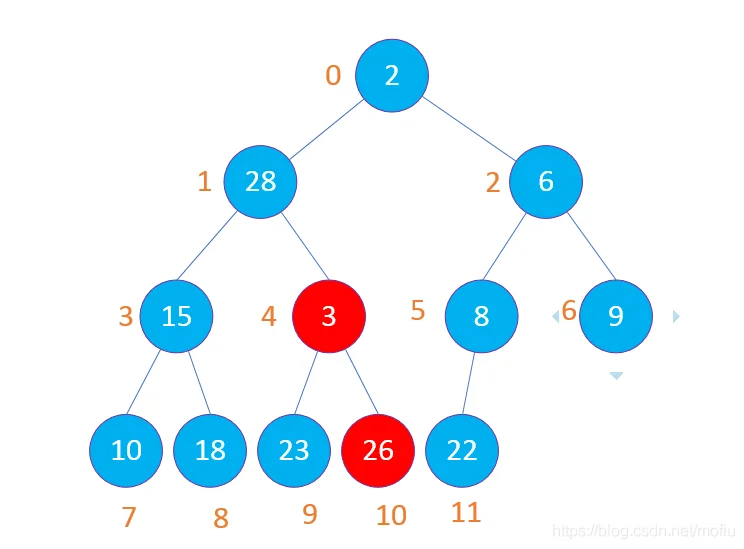
然后选择3节点,(3,7,8)节点比较,先比较7和8节点,选择较小的节点与3节点比较,结果如下图
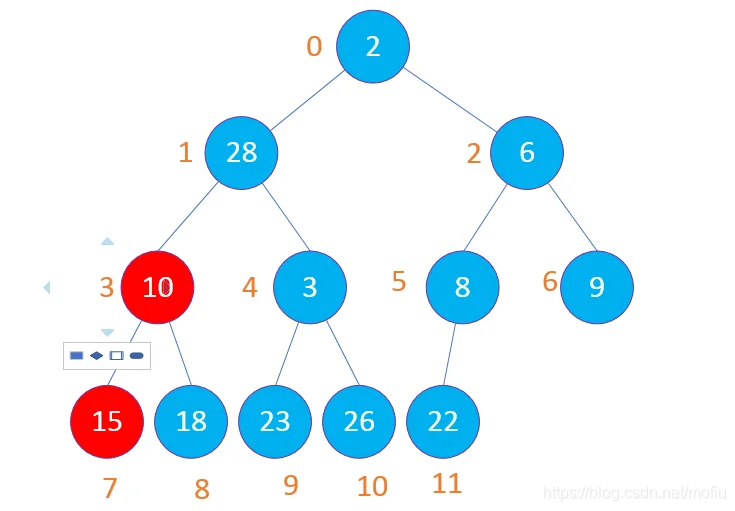
接下来比较root节点为2,child为5和6的几个几点。选择5和6中较小的节点与5(root节点)比较,2和5进行交换,交换后不确定5为root(11为子节点)的子节点是否都大于5的值,所以也进行比较一次。
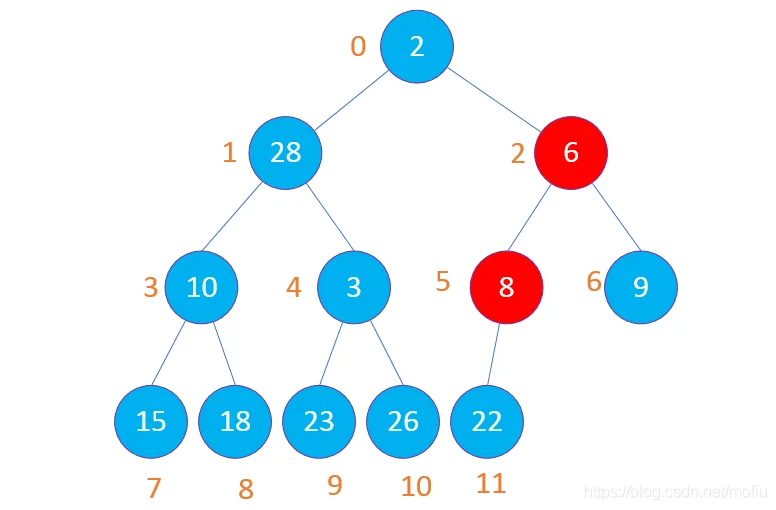
接下来对(1,3,4节点比较)较小的节点4与父节点1进行交换
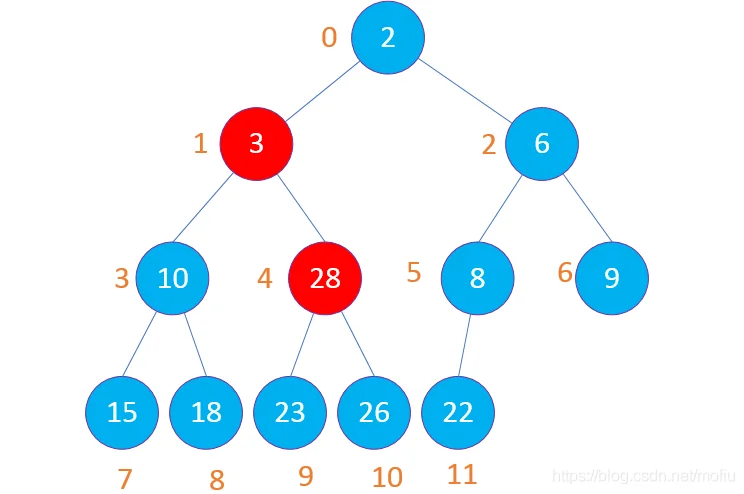
1和4交换后后,4、9、10已经不符合小顶堆的特性了,所以需要重新比较,此时4节点就变成了9和10的root节点
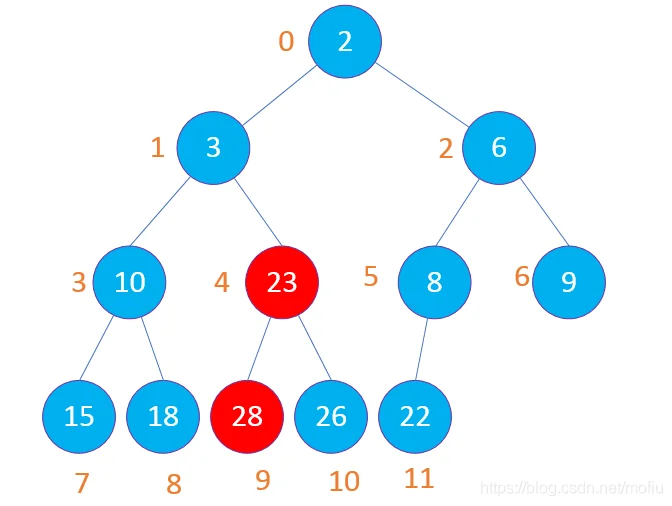
小顶堆构建完成
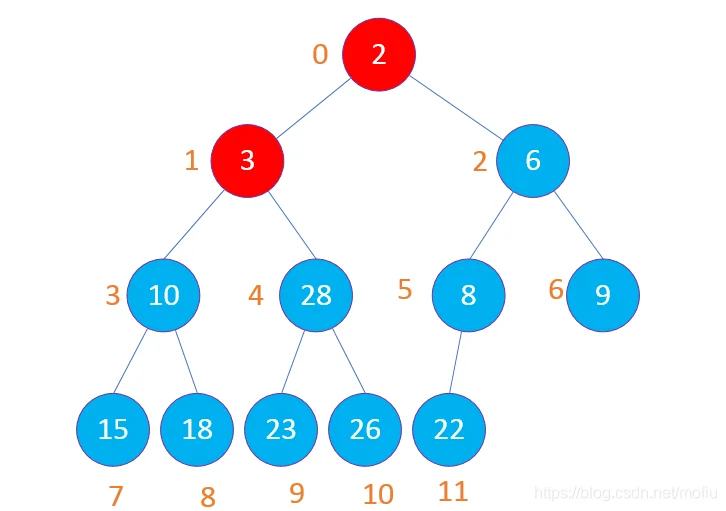
2、排序过程
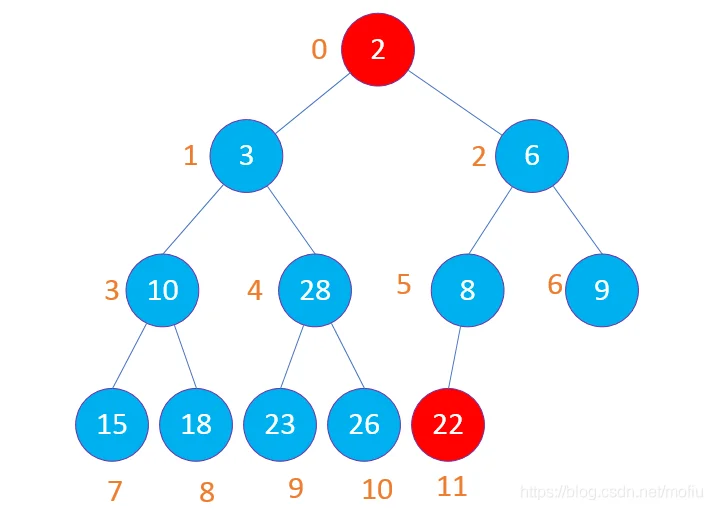
首先将堆顶的最小值与最后一个值交换(数组中的0和11位置交换),交换后重新构建堆(11位置已经是最小的值,不参与堆的构建,所以重新构建堆的数组要减去最后的值),如此往返,排序就完成了。
三、代码
func minHeap(root int, end int, c []int) {
for {
var child = 2*root + 1
//判断是否存在child节点
if child > end {
break
}
//判断右child是否存在,如果存在则和另外一个同级节点进行比较
if child+1 <= end && c[child] > c[child+1] {
child += 1
}
if c[root] > c[child] {
c[root], c[child] = c[child], c[root]
root = child
} else {
break
}
}
}
//降序排序
func HeapSort(c []int) {
var n = len(c)-1
for root := n / 2; root >= 0; root-- {
minHeap(root, n, c)
}
fmt.Println("堆构建完成")
for end := n; end >=0; end-- {
if c[0]<c[end]{
c[0], c[end] = c[end], c[0]
minHeap(0, end-1, c)
}
}
}
四、扩展问题
如果需要找出100w个数值中100个最大的数怎么找出呢,?
思路1: 将所有值构建大顶堆,然后排序,排序只排出100个大的值即可
思路2: 因为找出100个最大的值,不需要排序,所以可以只建一个100的数的小顶堆,然后将数组的后边的数逐一和堆顶最小值比较,如果大于堆顶的值就进行交换并重新构建堆**,如果小于顶堆的话就进行下一次比较(不重建堆)**
//在c数组中找出num个最大值
func HeapSort(c []int,num int) []int {
m:=len(c)-1
createHeap(c[:num],num-1)
fmt.Println("堆构建完成")
for i := num; i <=m; i++ {
if c[0]<c[i]{
c[0],c[i] = c[i],c[0]
createHeap(c[:num],num-1)
}
}
fmt.Println(c[:num])
return c
}
func createHeap(arr []int,end int){
for start := end / 2; start >= 0; start-- {
minHeap(start, end, arr)
}
}
//随机数组生成
func generateRandomNumber(start int, end int, count int) []int {
//范围检查
if end < start || (end-start) < count {
return nil
}
//存放结果的slice
nums := make([]int, 0)
r := rand.New(rand.NewSource(time.Now().UnixNano()))
for len(nums) < count {
num := r.Intn((end - start))
exist := false
for _, v := range nums {
if v == num {
exist = true
break
}
}
if !exist {
nums = append(nums, num)
}
}
return nums
}
