算法描述
我们以大根堆举例,堆其实就是完全二叉树,大根堆的堆顶是堆中的最大元素,大根堆的父节点比左右两个孩子都大:
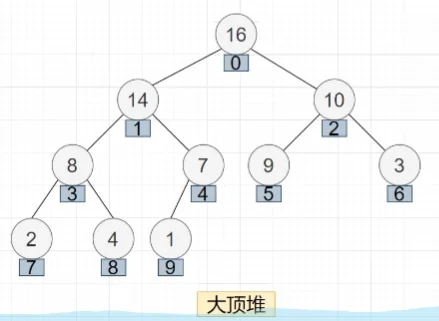
看完大根堆的结构之后,我们其实还需要将大根堆中的元素都存到数组中,比如上面结构的大根堆对应的数组如下所示:

同时用数组储存大根堆还有一些规则:

大根堆的维护
如果大根堆中的元素不满足大根堆的性质,就要进行堆的维护。比如下图中的红色节点,节点值为4,此时就不满足对的性质了(孩子节点的值比父节点大),需要进行堆的维护。
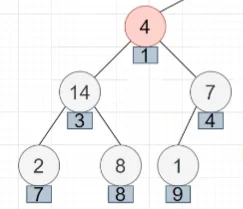
首先将父节点与左孩子进行交换:
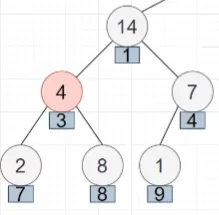
接着还需要对左孩子进行堆的维护,因为交换之后,左孩子与它自己的孩子就违反了堆的性质,我们将左孩子与它的右孩子进行交换,就完成了堆的维护:
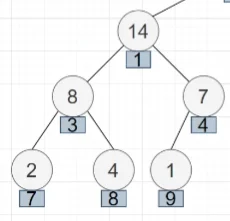
递归O(logN)以下是堆维护的代码:
func heapify(arr []int, n int, i int) {
//堆的维护
largest := i //i为当前父节点的下标
lson := i * 2 + 1 //左孩子
rson := i * 2 + 2 //右孩子
// 保存最大值的下标
if lson < n && arr[largest] < arr[lson] {
largest = lson
}
if rson < n && arr[largest] < arr[rson] {
largest = rson
}
if largest != i {
arr[largest], arr[i] = arr[i], arr[largest]
// 往孩子节点递归维护堆
heapify(arr, n, largest)
}
}
建堆
建堆以下面这个无序数组为例:
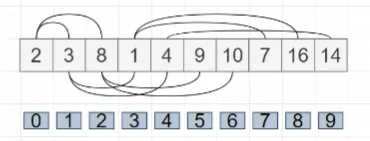
堆的初始状态是这样的:
n / 2 - 1n / 2 - 10所以建堆的代码:
// 建堆
// 从最后一个元素的父节点进行建堆(第一次堆的维护)
for i := n / 2 - 1; i >= 0; i-- {
heapify(arr, n, i)
}
堆排序
建立好大根堆之后,我们需要进行堆排序,其实就是每次将堆顶元素放到数组的后面(将数组中的当前元素与数组末尾的元素做交换),同时进行堆的维护,这样每一次操作之后堆顶元素始终是堆中的最大元素,那么当结束这个过程之后,数组就是一个递增的有序数组。
堆排序的代码:
// 排序
// 每次将堆的最后一个元素与堆顶元素交换,然后从堆中删除最后一个元素放到数组的最后一位
// 堆顶元素就是每次维护结束以后堆中最大的元素
// 到最后数组就会从小到大排序
for i := n - 1; i > 0; i-- {
arr[i], arr[0] = arr[0], arr[i]
// 交换元素以后要进行堆的维护
heapify(arr, i, 0)
}
完整代码
package main
import "fmt"
func heapify(arr []int, n int, i int) {
//堆的维护
largest := i //i为当前父节点的下标
lson := i * 2 + 1 //左孩子
rson := i * 2 + 2 //右孩子
// 保存最大值的下标
if lson < n && arr[largest] < arr[lson] {
largest = lson
}
if rson < n && arr[largest] < arr[rson] {
largest = rson
}
if largest != i {
arr[largest], arr[i] = arr[i], arr[largest]
// 往孩子节点递归维护堆
heapify(arr, n, largest)
}
}
func HeapSort(arr []int, n int) {
// 建堆
// 从最后一个元素的父节点进行建堆(第一次堆的维护)
for i := n / 2 - 1; i >= 0; i-- {
heapify(arr, n, i)
}
// 排序
// 每次将堆的最后一个元素与堆顶元素交换,然后从堆中删除最后一个元素放到数组的最后一位
// 堆顶元素就是每次维护结束以后堆中最大的元素
// 到最后数组就会从小到大排序
for i := n - 1; i > 0; i-- {
arr[i], arr[0] = arr[0], arr[i]
// 交换元素以后要进行堆的维护
heapify(arr, i, 0)
}
}
func main() {
arr := []int{1, 9, 10, 30, 2, 5, 45, 8, 63, 234, 12}
HeapSort(arr, len(arr))
fmt.Println(arr)
}
输出结果:
[1 2 5 8 9 10 12 30 45 63 234]
