堆排序是一种漂亮的排序算法。它使用一个最大堆对一系列数字或其他定义了顺序关系的元素进行排序。在这篇文章里,我们将深入探究 Go 标准库中堆排序的实现。
最大堆
First a short recap on . A max-heap is a container that provides its maximum element in O(1) time, adds an element in O(log n), and removes the maximum element in O(log n).
首先来简单重述一下 。最大堆是一个容器,能在 O(1) 时间内取出最大元素,在 O(log n) 的时间内增加一个元素,删除最大元素也是 O(log n) 时间。
最大堆是近似满二叉树,它的每个节点都大于或等于其子节点。在这篇文章中,我将后者称之为堆特性。
这两个特性一起定义出一个最大堆:
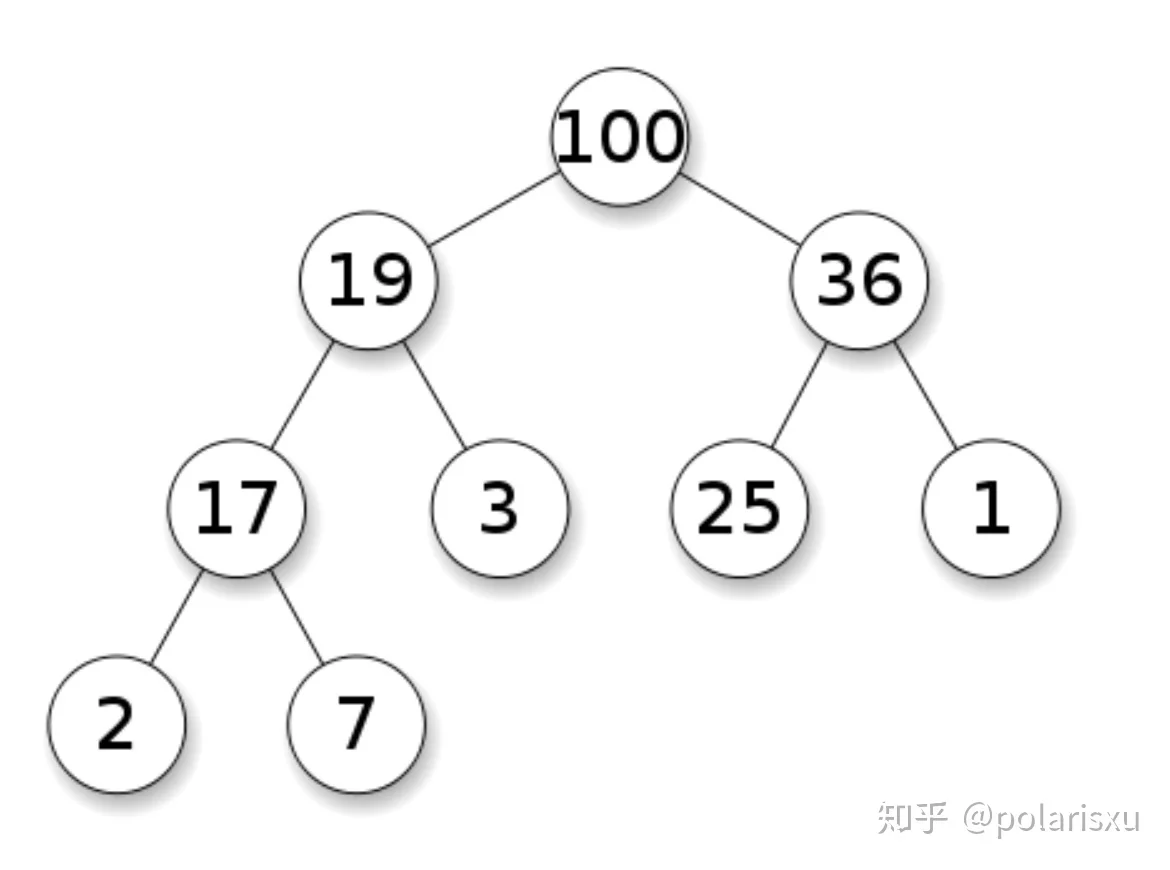
一个最大堆 . By Ermishin — Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=12251273
i2*i+12*i+2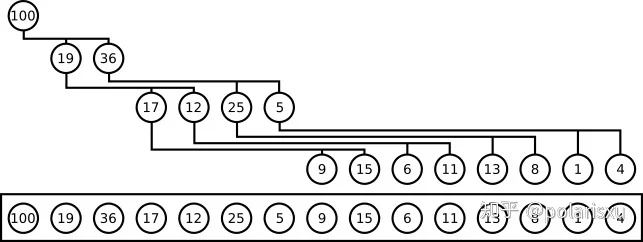
用一个数组表示最大堆 . By Maxiantor — Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=55590553
构建一个堆
一个数组可以在 O(n) 时间内转换成一个最大堆。很神奇,是不是?算法如下:
- 将输入数组看作一个堆。它尚未满足堆特性。
- 从倒数第二层开始对堆上的节点进行遍历 —— 即叶节点上面的一层 —— 直到根节点。
- 对每个节点,将它向下传送,直到它已经比它的两个子节点都大。向下传送时,总是与较大的子节点进行交换。
就是这样,你做到了!
为什么可行?我将试图用这个大手一挥的证据让你信服(如果想跳过,请随意):
xxxxx这对堆上的每个节点都是成立的,包括根节点。
堆排序算法
现在开始正课 —— 堆排序。
堆排序的工作过程分两个步骤:
- 使用上面展示的算法,从输入数组构建一个最大堆。这需要 O(n) 的时间。
- 从堆中弹出元素放到输出数组中,从后往前填充。每次从堆中弹出元素需要 O(log n) 时间,整个容器加起来为 O(n * log n)。
Go 实现的一个很酷的特性,是它使用输入数组来存放输出,因此避免了为输出分配 O(n) 的内存。
堆排序的实现
Go 的排序库支持任何 索引为整数,元素之间有 定义好的顺序关系,并且支持在两个索引之间交换元素的集合。
自然地,任何数字组成的连续容器都可以满足这个接口。
heapSort函数的签名有点晦涩,不过看了前三行就清楚了:
abdataheapSort(data, a, b)[a, b)firstalohialohi接下来的代码构建最大堆:
shiftDown()shiftDown()data接下来,我们弹出所有元素来创建一个有序的数组。
ifirstfirsti换句话说,我们从后往前填充数组,从最大的元素开始,直到倒数第二小的元素。结果就是将输入数组进行了排序。
维持堆特性
shitDown()root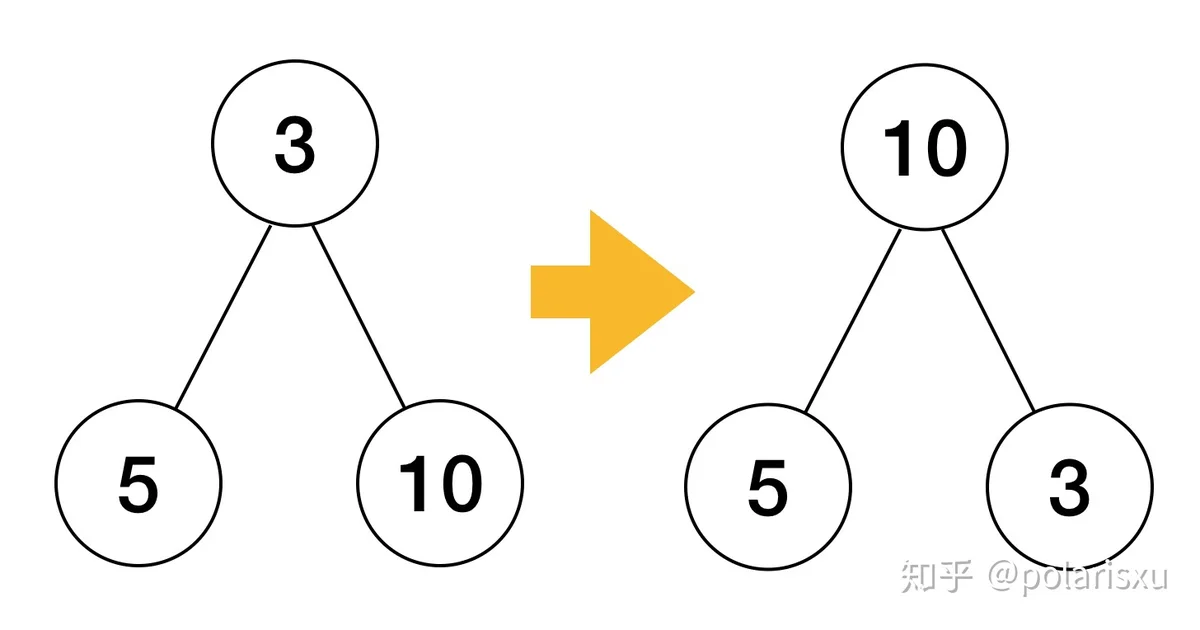
310前面的几行计算第一个子节点的索引并确认它存在:
child >= hiroot接下来,我们选两个子节点中较大的一个。
child++然后,我们检查一下父节点是否确实比子节点小:
如果父节点比它的最大子节点要大,我们就搞定,所以返回。
root结论
这是第三篇针对我读到的不熟悉的代码片段进行解释而写的文章。我喜欢这样的体验,因为它教会我如何读代码并就此进行交流。请在下面留下你的评论和反馈。
本文由 原创编译, 荣誉推出
